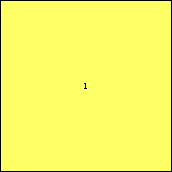Problem of the Month (January 2004)

What is the side of the smallest square s(n) that squares of areas 1, 2, 3, ... n can be packed into without overlap? The answers are pretty easy to find and prove for small n. What are the best packings you can find for larger values of n? How many of them can you prove are optimal? Can you pack squares of area 1 through 11 inside a square of side 8.5? Are there values of n where the optimal packings involve tilted squares? Does s(n) ≈ n/√2 ?

ANSWERS

Joseph DeVincentis and Philippe Fondanaiche succeeded in packing 11 squares into a square of side less than 8.5. They both sent me several small packings, but nothing that improved the best known bounds.

David W. Cantrell improved my best packings for n=9, 10, 12, 13, 14, 15, 16, 17, 18, 20, and 21, and then did n=22, 23, and 24!

Then in 2011, Maurizio Morandi improved several packings.

Here are the best known packings:

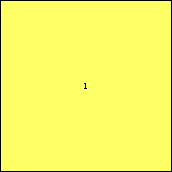
s(1) = √1 = 1.000
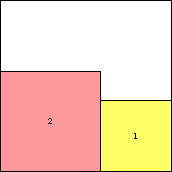
s(2) = √2+√1 = 2.414+
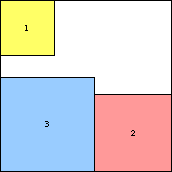
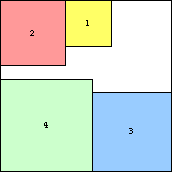
s(3) = √3+√2 = 3.146+
s(4) = √4+√3=3.732+

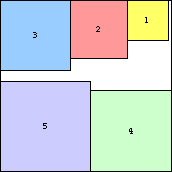
s(5) = √5+√4 = 4.236+
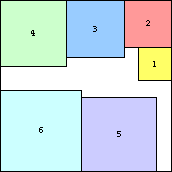
s(6) = √4+√3+√2 = 5.146+
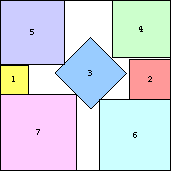
s(7) ≤ √6+√5+√(3/2) = 5.910+
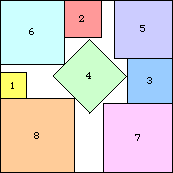
s(8) ≤ √7+√5+√3 = 6.613+

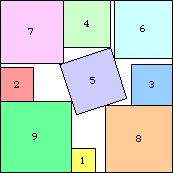
s(9) ≤ 7.246+
(DC)
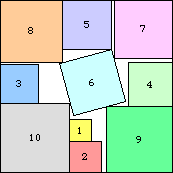
s(10) ≤ 7.829+
(DC)
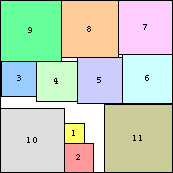
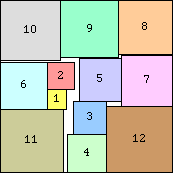
s(11) ≤ √9+√8+√7 = 8.474+

s(12) ≤ √10+√9+√8 = 8.990+
(DC)

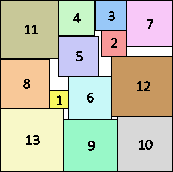
s(13) ≤ √12+√10+√3+√2 = 9.772+
(MM)
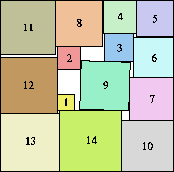
s(14) ≤ 10.510+
(MM)
s(15) ≤ √13+√9+√6+√5 = 11.291+
(MM)
s(16) ≤ √14+√10+√7+√6 = 11.999+
(MM)

s(17) ≤ √14+√10+√9+√8 = 12.732+
(MM)
s(18) ≤ √15+√11+√10+√9 = 13.351+
(MM)
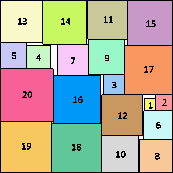
s(19) ≤ √19+√18+√12+√4 = 14.065+
(MM)
s(20) ≤ √17+√15+√8+√6+√2 = 14.688+
(MM)

s(21) ≤ √21+√20+√11+√9 = 15.371+
(MM)
s(22) ≤ √19+√18+√16+√12 = 16.065+
(MM)
s(23) ≤ √23+√22+√17+√10 = 16.771+
(MM)
s(24) ≤ √24+√23+√20+√11 = 17.483+
(MM)
Sasha Ravsky notes that s(n) must be at least √n+√(n–1), and this is enough to prove the values of s(n) for n≤5. He also notes that a collection of squares with total area S and the side of the largest square x can always be packed inside a square of side x+√(S–x²) without tilting any squares. Thus √(n(n+1)/2) ≤ s(n) ≤ √n + √(n(n–1)/2).

Philippe Fondanaiche managed to pack squares of areas 1 through 100 inside a square of side 71.647+, with less than 2% wasted area. But then David W. Cantrell packed them inside a square of side 71.344+, with less than .8% wasted area!

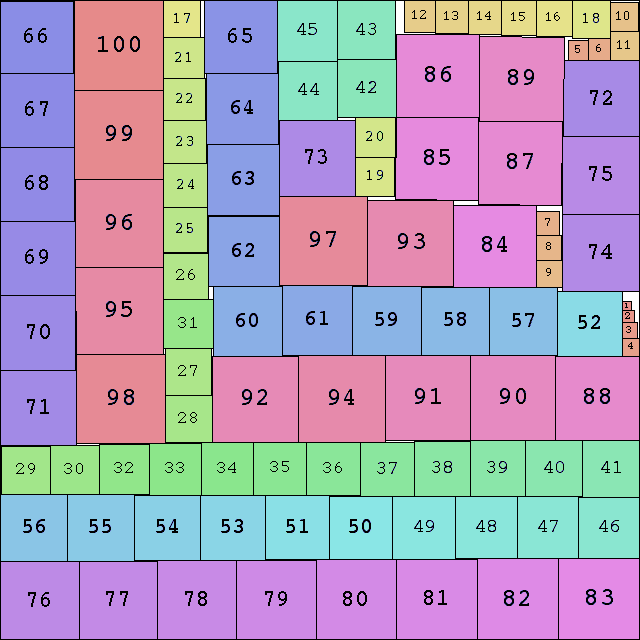
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 1/8/11.

s(1) = √1 = 1.000	s(2) = √2+√1 = 2.414+	s(3) = √3+√2 = 3.146+	s(4) = √4+√3=3.732+
s(5) = √5+√4 = 4.236+	s(6) = √4+√3+√2 = 5.146+	s(7) ≤ √6+√5+√(3/2) = 5.910+	s(8) ≤ √7+√5+√3 = 6.613+
s(9) ≤ 7.246+ (DC)	s(10) ≤ 7.829+ (DC)	s(11) ≤ √9+√8+√7 = 8.474+	s(12) ≤ √10+√9+√8 = 8.990+ (DC)
s(13) ≤ √12+√10+√3+√2 = 9.772+ (MM)	s(14) ≤ 10.510+ (MM)	s(15) ≤ √13+√9+√6+√5 = 11.291+ (MM)	s(16) ≤ √14+√10+√7+√6 = 11.999+ (MM)
s(17) ≤ √14+√10+√9+√8 = 12.732+ (MM)	s(18) ≤ √15+√11+√10+√9 = 13.351+ (MM)	s(19) ≤ √19+√18+√12+√4 = 14.065+ (MM)	s(20) ≤ √17+√15+√8+√6+√2 = 14.688+ (MM)
s(21) ≤ √21+√20+√11+√9 = 15.371+ (MM)	s(22) ≤ √19+√18+√16+√12 = 16.065+ (MM)	s(23) ≤ √23+√22+√17+√10 = 16.771+ (MM)	s(24) ≤ √24+√23+√20+√11 = 17.483+ (MM)