Problem of the Month
(January 2008)
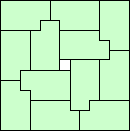
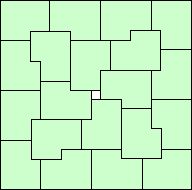
The problem of tiling equal polyominoes in squares has been well-studied. This month we investigate tiling equal polyominoes in frames, squares missing from the centers of squares. We also investigate tiling equal polyominoes in circles, a totally symmetric set of lattice points whose distance from the center is smaller than a constant. Can you find examples of the smallest frames or circles made from various polyominoes? What other shapes can be tiled well with equal polyominoes?
ANSWERS
Frame Tilings:
Small Polyominoes
Pentominoes
Hexominoes
Heptominoes
Octominoes
Nonominoes
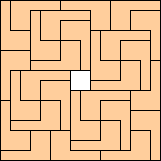
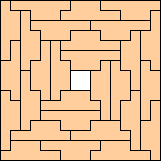
(George Sicherman)
| 
(George Sicherman)
| 
|
|
Decominoes
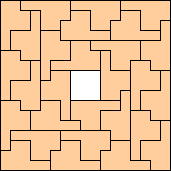
(George Sicherman)
| 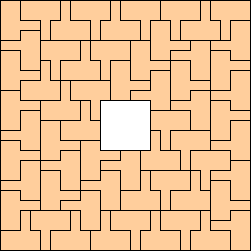
(George Sicherman)
|
|
Undecominoes
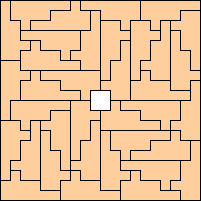
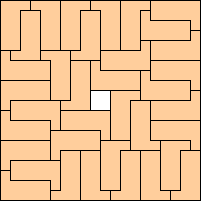
(George Sicherman)
| 
(George Sicherman)
|
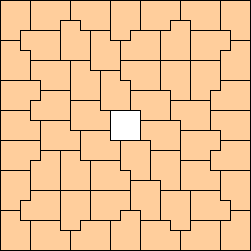
(George Sicherman)
|
|
Mike Reid gave these non-trivial frame tilings for some larger L polyominoes:
Off-Center Frame Tilings:
Small Polyominoes
Pentominoes
Hexominoes
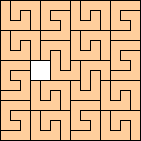
(George Sicherman)
| 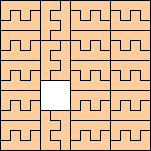
(George Sicherman)
| 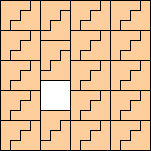
(George Sicherman)
|
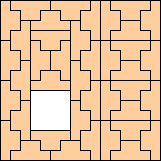
(George Sicherman)
| 
(George Sicherman)
|
|
Heptominoes
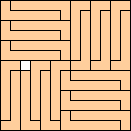
(George Sicherman)
| 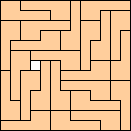
(George Sicherman)
|
|
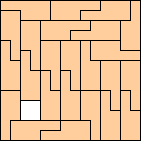
Octominoes
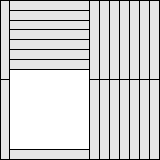
| 
(George Sicherman)
|
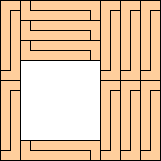
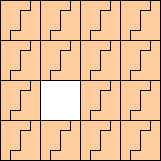
(George Sicherman)
| 
(George Sicherman)
| 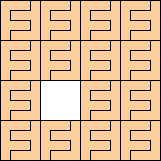
(George Sicherman)
|
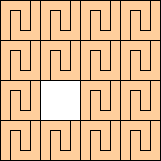
(George Sicherman)
| 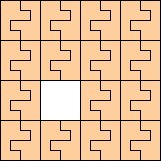
(George Sicherman)
| 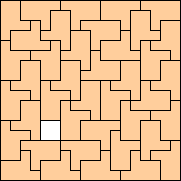
(George Sicherman)
|
|
Nonominoes
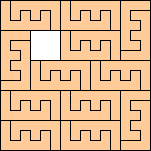
(George Sicherman)
| 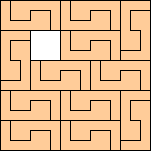
(George Sicherman)
| 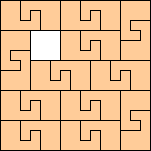
(George Sicherman)
|
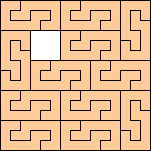
(George Sicherman)
| 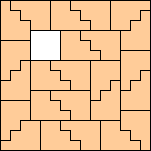
(George Sicherman)
| 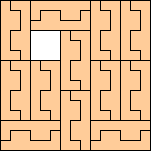
(George Sicherman)
|
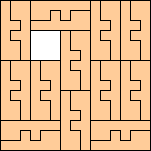
(George Sicherman)
| 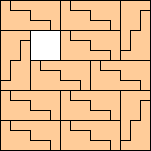
(George Sicherman)
| 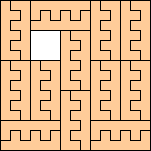
(George Sicherman)
|
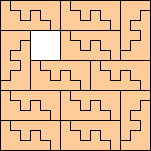
(George Sicherman)
| 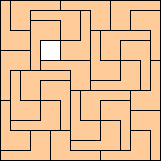
(George Sicherman)
| 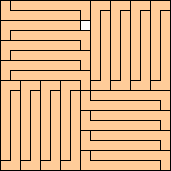
(George Sicherman)
|
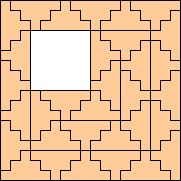
(George Sicherman)
| 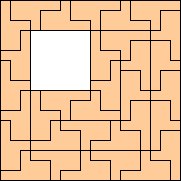
(George Sicherman)
| 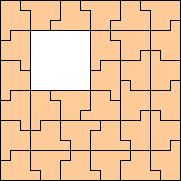
(George Sicherman)
|
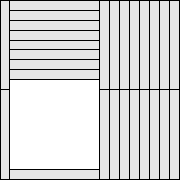
| 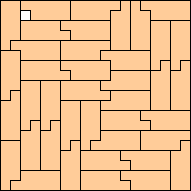
(George Sicherman)
|
|
George Sicherman investigated triangular frames made from polyiamonds...
...and hexagonal frames made from polyhexes:
Circular Tilings:
Small Polyominoes
Pentominoes
Hexominoes
Heptominoes
Octominoes
Nonominoes
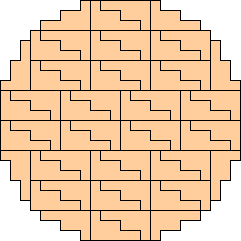
(George Sicherman)
|
|
Decominoes
Undecominoes
I also investigated tilings of donuts, circles missing from the centers of circles. I even allowed disconnected regions. My results are here.
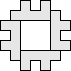
Claudio Baiocchi suggested that we look for full symmetry configurations. We call these Baiocchi figures.
Baiocchi Figures:
Small Polyominoes
Pentominoes

(George
Sicherman)
| 
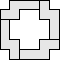
(George
Sicherman)
| 
| 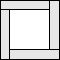
| 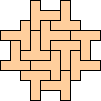
(George
Sicherman)
|
|
Hexominoes

| 
| 
| 
| 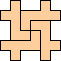
(George
Sicherman)
| 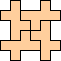
(George
Sicherman)
| 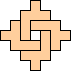
(George
Sicherman)
|
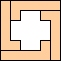
(George
Sicherman)
| 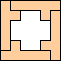
(George
Sicherman)
| 
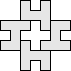
| 
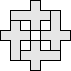
| 
| 
|
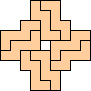
(George
Sicherman)
| 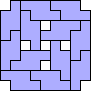
(Corey Plover)
| 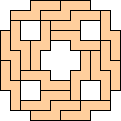
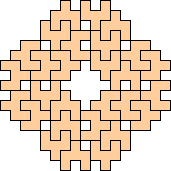
(George
Sicherman)
| 
(George
Sicherman)
|
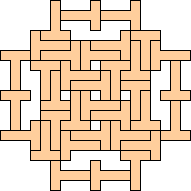
(George Sicherman)
| 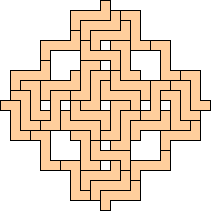
(George Sicherman)
| 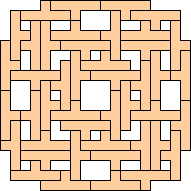
(George Sicherman)
|
|
George Sicherman also investigated Baiocchi figures made from other polyforms:
Polyiamonds
The 9-iamonds are here.
Polypents
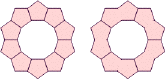
(Károly Hajba)
| 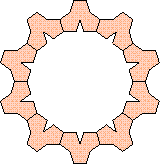
(George Sicherman)
| 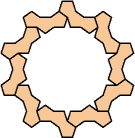
(George Sicherman)
|
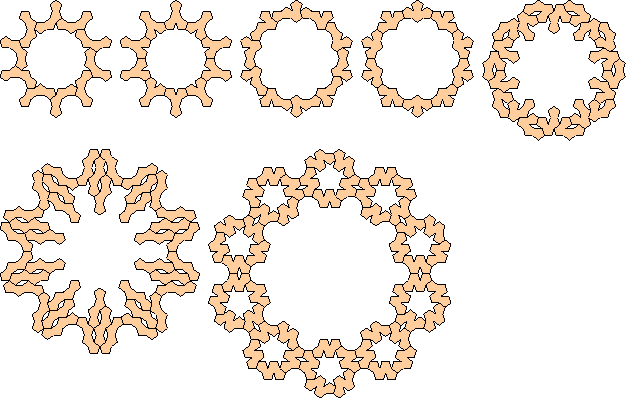
(George Sicherman)
|
|
The pentapents can be found here.
Polyhexes
The hexahexes can be found here.
Polyhepts
The pentahepts can be found here.
Polyocts
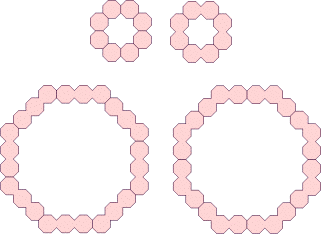
(Károly Hajba)
| 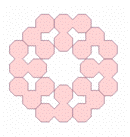
(Károly Hajba)
|
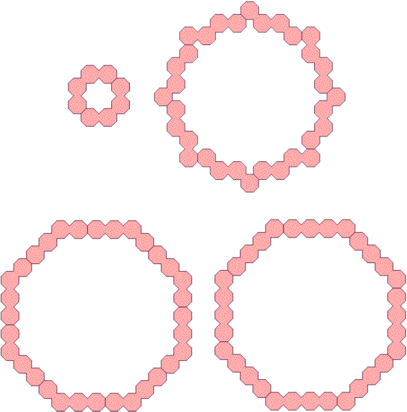
(Károly Hajba)
|
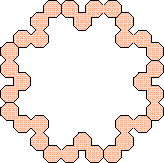
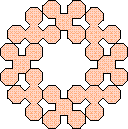
(George Sicherman)
| 
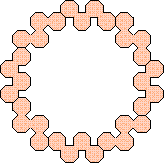
(George Sicherman)
| 
(George Sicherman)
|
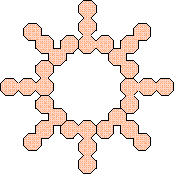
(George Sicherman)
| 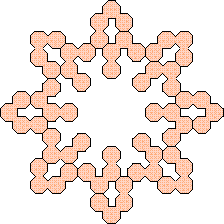
(George Sicherman)
|
|
The pentaocts can be found here.
The Baiocchi figures for polycubes can be found here.
If you can extend any of these results, please
e-mail me.
Click here to go back to Math Magic. Last updated 1/1/09.