Problem of the Month (January 2012)

You go to a pizza parlor and order a unit pizza cut into n equal slices. You only eat some of the pieces, and want to take m of them home in a square box with no overlap. What is the smallest box that will suffice?

ANSWERS

Solutions were sent by Maurizio Morandi, Joe DeVincentis, David Cantrell, Bryce Herdt, Dick Hess, Jeremy Galvagni, Symen Hovinga, and Theo Geerinck.

Smallest Known Packing of n Sectors of 1/m th of a Unit Circle
m \ n12345678
2
s = 1 + 1/√2 = 1.707+
 
s = 2
 
s = 1 + √2 = 2.414+
 
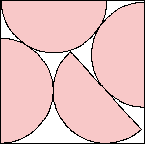
s = 2.724+
(MM)
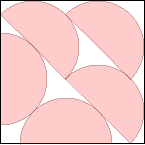
s = 1 + 3/√2 = 3.121+
 
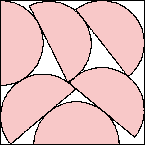
s = 3.380+
(DH)
s = 3.599+
(MM) after (DC)
s = 3.819+
(MM)
3
s=1+sin(π/12)=1.258+
 
s = (1 + √7)/2 = 1.822+
 
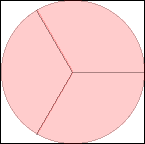
s = 2
 
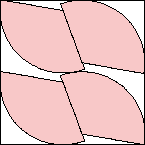
s = 2.309+
(MM)
s = 2.636+
(MM) after (EF)
s = 2.846+
(MM)
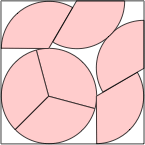
s = 2.999+
(DC) after (MM)
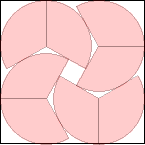
s = 2 + 2/√3 = 3.154+
 
4
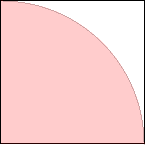
s = 1
 
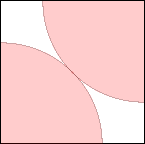
s = √2 = 1.414+
 
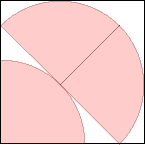
s = 1 + 1/√2 = 1.707+
 
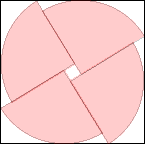
s = 1.942+
 
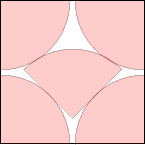
s=(3√2+√38)/5=2.081+
 
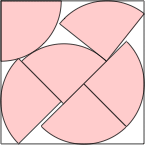
s = 2.375+
(DC) after (MM)
s = 2.594+
(MM)
s = 2.699+
(DC) after (MM)
5
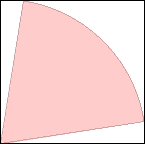
s = cos(π/20) = .987+
 
s = √2 = 1.414+
 
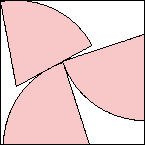
s = 1.673+
(MM)
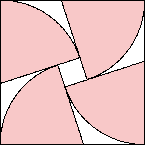
s=1+tan(π/5)=1.726+
(MM)
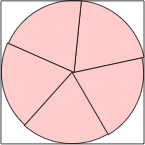
s = 1.997+
(MM) after (DC)
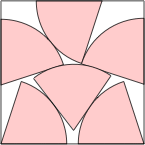
s = 2.176+
(DC) after (EF)
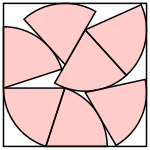
s = 2.331+
(SH) and (TG)
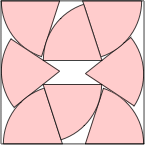
s = 2.439+
(DC) after (MM)
6
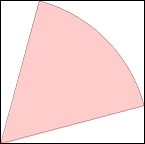
s = cos(π/12) = .965+
 
s = 1.244+
(MM)
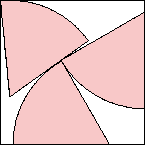
s = 1.491
(MM)
s = 1 + 1/√3 = 1.577+
(MM)
s = 1.833+
(MM)
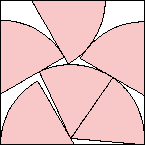
s = 1.951+
(MM)
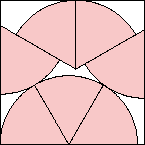
s = 2.096+
(MM)
s = 2.187+
(MM)
7
s = cos(3π/28) = .943+
 
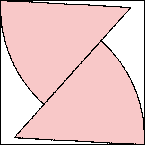
s = 1.109+
(MM)
s = 1.340+
(DC) after (MM)
s=1+tan(π/7)=1.481+
(MM)
s = 1.685+
(MM)
s = 1.815+
(MM)
s = 1.940+
(MM)
s = 2.021+
(MM)
8
s = cos(π/8) = .923+
 
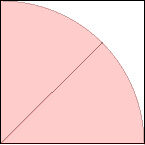
s = 1
 
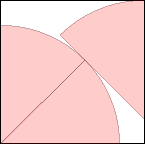
s=(1+√2)/2=1.207+
 
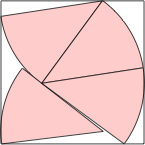
s = 1.398+
(DC) after (MM)
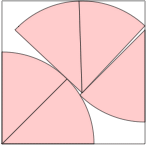
s = 1.554+
(DC) after (EF)
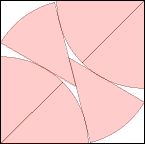
s=√(14-8√2)=1.638+
(MM) after (EF)
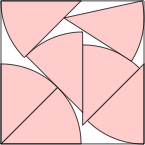
s = 1.786+
(DC)
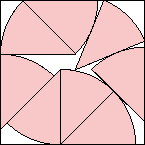
s = 1.915+
(MM)
9
s = cos(5π/36) = .906+
 
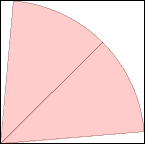
s = cos(π/36) = .996+
 
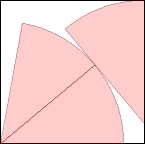
s = 1.166+
 
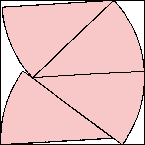
s = 1.282+
(MM)
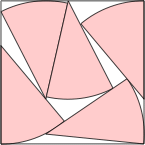
s = 1.456+
(DC) after (JD)
s = 1.551+
(MM)
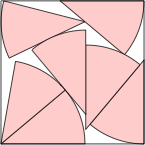
s = 1.704+
(DC)
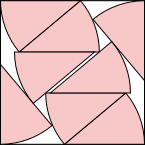
s = 1.798+
(JD)
10
s = cos(3π/20) = .891+
 
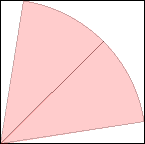
s = cos(π/20) = .987+
 
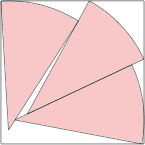
s = 1.108+
(DC) after (JD)
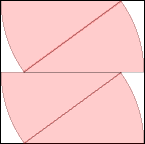
s = 1.184+
 
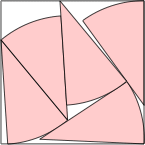
s = 1.371+
(DC) after (JD)
s = 1.472+
(MM)
s = 1.594+
(MM)
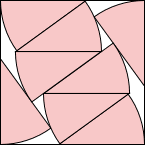
s = 1.681+
(JD)

Bryce Herdt asks a couple questions:

Is there a limiting value for n=m? Seems to me it should be √π. Jeremy Galvagni sent the construction below, which might work. He also notes that if m/n → 2/π, the slices can be placed alternately up and down to fit inside a square of side approaching 1.

Clearly s is increasing in n and decreasing in m, but are these always strict? I'll guess yes. Does anyone have a counterexample?

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 1/26/12.