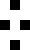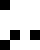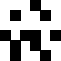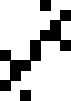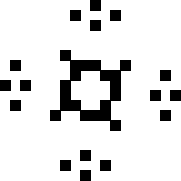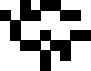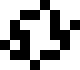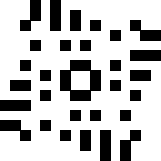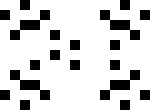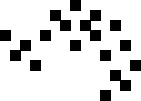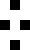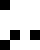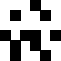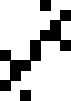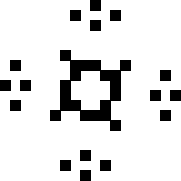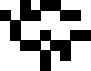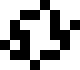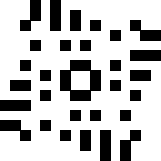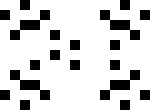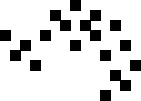Problem of the Month (January 2015)
Conway's Game of Life is the most famous cellular automaton. The live cells in generation n+1 are precisely those with 3 live neighbors in generation n, or 2 live neighbors in generation n if the cell was already alive in generation n. Here "neighbors" means the places a king could move in chess.
This month we consider a variant of this game which we call "Knight Life", which uses the same growth rules, but in which the 8 neighbors of a cell are the places a knight could move in chess.
What life forms are stable ("still life")? What life forms repeat themselves with a period larger than 1? What periods are possible? Are there life forms that maintain the same shape but move ("gliders")? Are there life forms that grow without bound? What is the life form that starts inside a rectangle of a certain size that lasts the longest before dying or repeating? Is there a "garden of Eden" configuration that has no prior generation?
ANSWERS
Contributors this month include George Sicherman, Joe DeVincentis, and Berend van der Zwaag.
Known Periods
| Period | First Configuration Found | Author
|
| 1 | 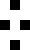 | Erich Friedman
|
| 2 | 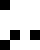 | Erich Friedman
|
| 3 |  | George Sicherman
|
| 4 | 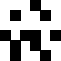 | Erich Friedman
|
| 5 | 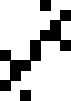 | George Sicherman
|
| 6 |  | Erich Friedman
|
| 7 | 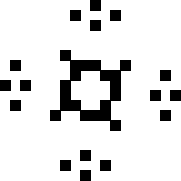 | George Sicherman
|
| 8 | 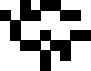 | George Sicherman
|
| 9 |  | George Sicherman
|
| 10 | 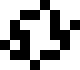 | George Sicherman
|
| 11 | 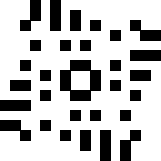 | George Sicherman
|
| 12 | 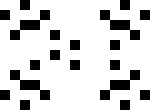 | Joe DeVincentis
|
| 13 | ? | ?
|
| 14 |  | George Sicherman
|
| 22 |  | George Sicherman
|
| 24 | 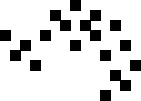 | George Sicherman
|
Smallest Known Still Life
Smallest Known Period 2
| 4
| 
|
| 8
| 
| 
(George Sicherman)
| 
(George Sicherman)
| 
(George Sicherman)
| 
(George Sicherman)
| 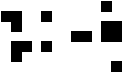
(George Sicherman)
|

(George Sicherman)
| 
(George Sicherman)
| 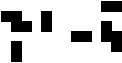
(George Sicherman)
| 
(George Sicherman)
| 
(Joe DeVincentis)
| 
(Joe DeVincentis)
|
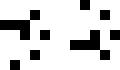
(Joe DeVincentis)
| 
(Joe DeVincentis)
| 
(Joe DeVincentis)
| 
(Joe DeVincentis)
| 
(Joe DeVincentis)
| 
(Joe DeVincentis)
|

(Joe DeVincentis)
| 
(Joe DeVincentis)
| 
(Joe DeVincentis)
| 
(Joe DeVincentis)
| 
(Joe DeVincentis)
| 
(Joe DeVincentis)
|

(Joe DeVincentis)
| 
(Joe DeVincentis)
| 
(Joe DeVincentis)
| 
(Joe DeVincentis)
| 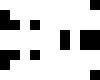
(Joe DeVincentis)
|
|
Period 3 with Reflectional Symmetry
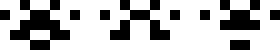
(George Sicherman)
| 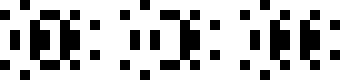
(Joe DeVincentis)
| 
(Joe DeVincentis)
|

(George Sicherman)
| 
(George Sicherman)
|
|
Period 3 with Horizontal and Vertical Symmetry
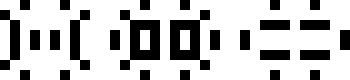
(Joe DeVincentis)
| 
(Joe DeVincentis)
| 
(Joe DeVincentis)
|
|
Period 3 with 90o Rotational Symmetry

(George Sicherman)
| 
(George Sicherman)
|

(George Sicherman)
| 
(George Sicherman)
|
|
Period 3 with Full Symmetry

(George Sicherman)
|
|
Other Period 3

(George Sicherman)
|
|
Smallest Known Period 4
| 11
| 
| 
(Joe DeVincentis)
| 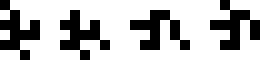
(Joe DeVincentis)
|
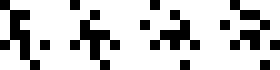
(Joe DeVincentis)
| 
(Joe DeVincentis)
| 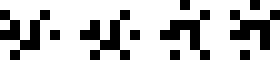
(Joe DeVincentis)
|

(Joe DeVincentis)
| 
(Joe DeVincentis)
| 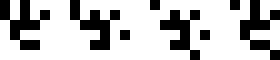
(Joe DeVincentis)
|

(Joe DeVincentis)
| 
(Joe DeVincentis)
| 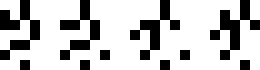
(Joe DeVincentis)
|

(Joe DeVincentis)
| 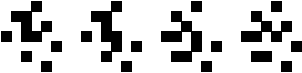
(George Sicherman)
|
| 11/12
| 
(Joe DeVincentis)
|
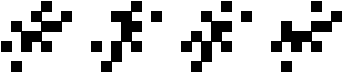
(George Sicherman)
| 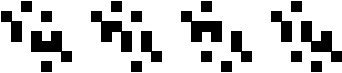
(George Sicherman)
| 
(George Sicherman)
|
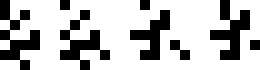
(Joe DeVincentis)
|
|
Smallest Known Period 4 with Reflectional Symmetry

(Joe DeVincentis)
| 
(Joe DeVincentis)
| 
(Joe DeVincentis)
|
|
Period 4 with 180o Rotational Symmetry

(George Sicherman)
| 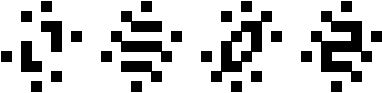
(George Sicherman)
| |
Period 4 with 90o Rotational Symmetry
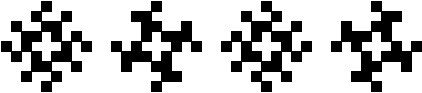
(George Sicherman)
| |
Period 4 with Reflectional
Symmetry after 2 Generations

| 
(George Sicherman)
| |
Period 4 with Horizontal and Vertical Symmetry
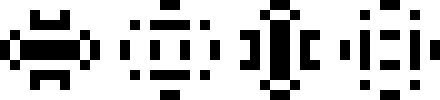
(Joe DeVincentis)
| 
(Joe DeVincentis)
|

(Joe DeVincentis)
| 
(George Sicherman)
|

(George Sicherman)
| 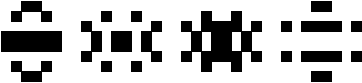
(George Sicherman)
|
|
Period 4 with Full Symmetry

(George Sicherman)
| 
(George Sicherman)
| |
Period 5 with Reflectional Symmetry

(George Sicherman)
| |
Period 5 with 90o Rotational Symmetry

(George Sicherman)
| 
(George Sicherman)
| 
(George Sicherman)
| 
(George Sicherman)
| 
(George Sicherman)
| 
(George Sicherman)
| |
Period 5 with 180o Rotational Symmetry

(George Sicherman)
| 
(George Sicherman)
| |
Period 5 with Horizontal and Vertical Symmetry

(George Sicherman)
| 
(George Sicherman)
| |
Period 5 with Full Symmetry

(George Sicherman)
| |
Smallest Known Period 6
| 9/10/13
| 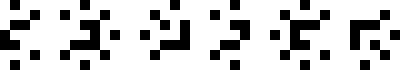
| 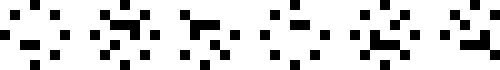
|
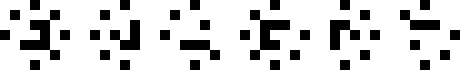
| 
(George Sicherman)
|
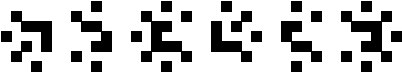
(George Sicherman)
| 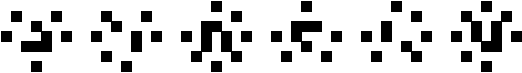
(George Sicherman)
|

(Joe DeVincentis)
| 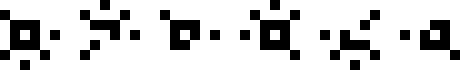
(Joe DeVincentis)
|

(Joe DeVincentis)
| 
(Joe DeVincentis)
|

(Joe DeVincentis)
| 
(Joe DeVincentis)
|

(Joe DeVincentis)
| 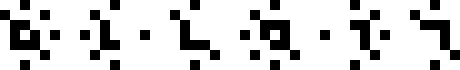
(Joe DeVincentis)
|

(Joe DeVincentis)
| 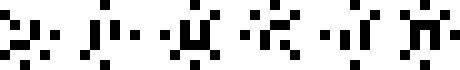
(Joe DeVincentis)
|

(Joe DeVincentis)
| 
(Joe DeVincentis)
|

(Joe DeVincentis)
| 
(Joe DeVincentis)
|

(Joe DeVincentis)
| 
(Joe DeVincentis)
|
|
Period 6 with Reflectional Symmetry

(George Sicherman)
| 
(George Sicherman)
| 
(George Sicherman)
| 
(George Sicherman)
| 
(George Sicherman)
| |
Period 6 with Horizontal and Vertical Symmetry
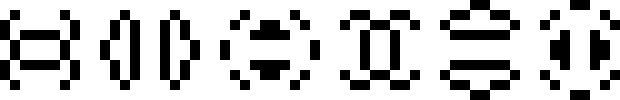
(George Sicherman)
| |
Period 6 with Full Symmetry

(George Sicherman)
| |
Period 7

(George Sicherman)
| 
(George Sicherman)
| 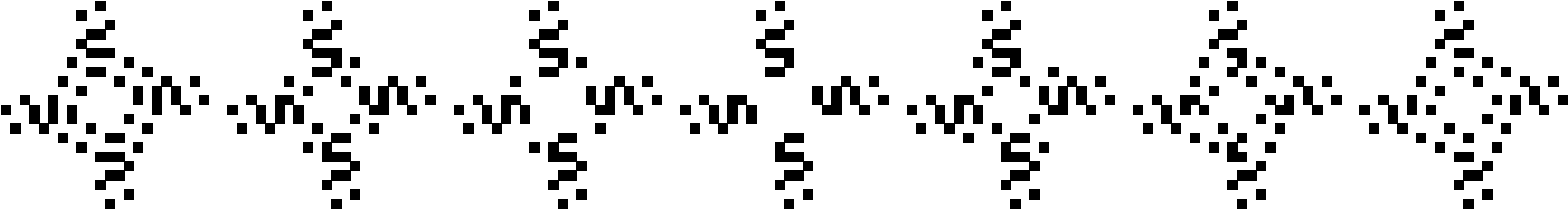
(George Sicherman)
| 
(George Sicherman)
| |
Period 8 with 180o Rotational Symmetry
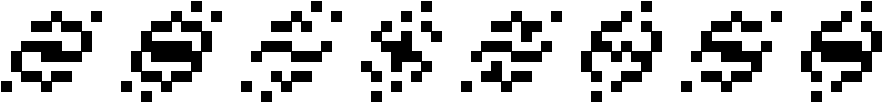
(George Sicherman)
| |
Period 8 with 90o Rotational Symmetry
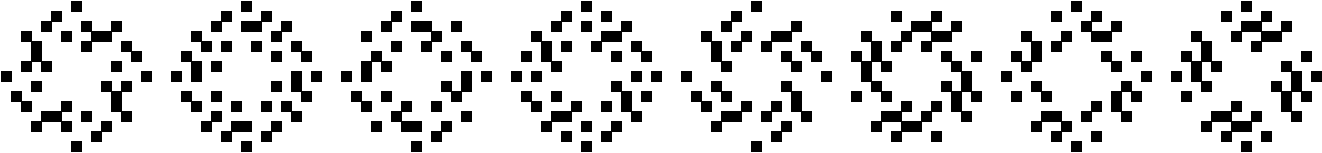
(George Sicherman)
| 
(George Sicherman)
| 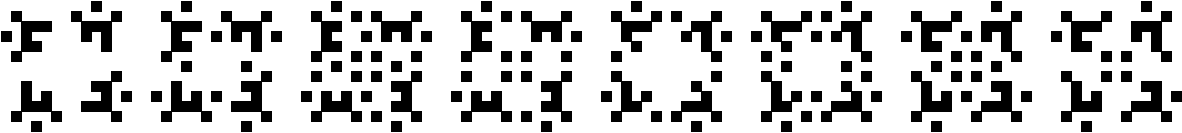
(George Sicherman)
| |
Period 8 with Full Symmetry

(George Sicherman)
| |
Other Period 8
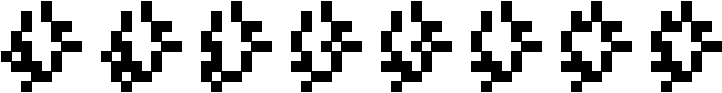
(George Sicherman)
| |
Period 9
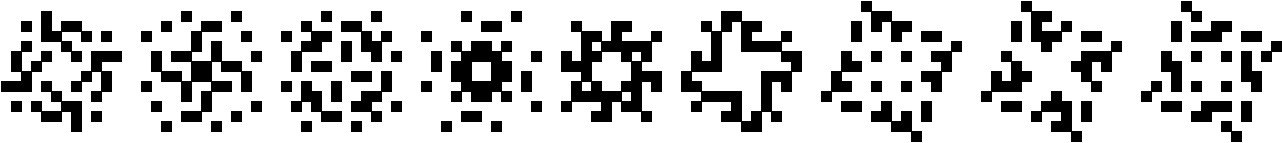
(George Sicherman)
| |
Period 10
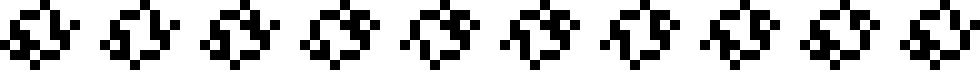
(George Sicherman)
| 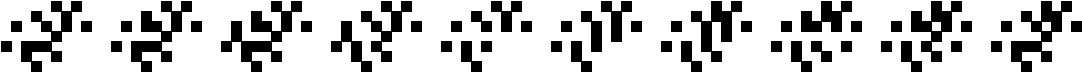
(George Sicherman)
| 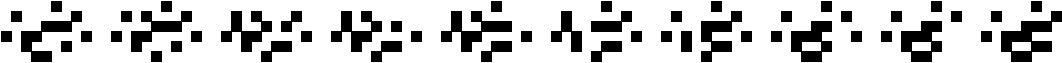
(George Sicherman)
| 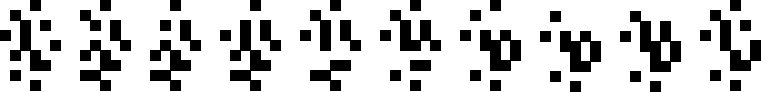
(George Sicherman)
| |
Larger Periods
Life Starting Inside m×n Grid
Lasting the Largest Known Number of
Generations Before Becoming Periodic
| m \ n | 3 | 4 | 5 | 6 | 7
|
|---|
| 3 | 
4
(GS)
|
|---|
| 4 | 
9
(GS) | 
28
(GS)
|
|---|
| 5 | 
17
(GS) | 
71
(GS) | 
95
(GS)
|
|---|
| 6 | 
42
(GS) | 
290
(GS) | 
305
(GS) | 
375
(GS)
|
|---|
| 7 | 
73
(GS) | ? | ? | ? | ?
|
|---|
George Sicherman was interested in larger compact configurations that lasted a long time. He found this configuration that lasted 4829 generations until it stabilized:

Berend van der Zwaag found that most random 60×60 configurations died out or stabilized, but most random 70×70 grew without bound.
If you can extend any of these results, please
e-mail me.
Click here to go back to Math Magic. Last updated 1/11/15.