Problem of the Month (January 2020)

The problem of packing circles in squares is perhaps the best studied problem in packing. Some results can be found on this packing page. This month we modify the problem slightly. What is the largest side s with the property that we can pack n unit circles inside a square of side s–ε so that no more than k other larger circles will also fit? What if we use squares or equilateral triangles instead of circles? This is similar to our math magic problem of February 2008.

ANSWERS

Solutions were received from Maurizio Morandi and Andrew B. Hudson.

Placing n Circles So That 0 More Fit
n=0

s = 2 		n=1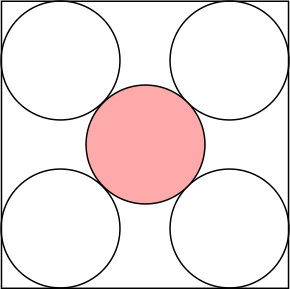

s = 2 + 2 √2 = 4.828+ 		n=2

s = 2 + 2 √3 = 5.464+ 		n=3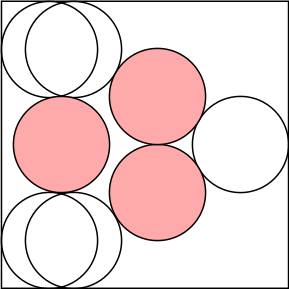

s = 5.969+ 		n=4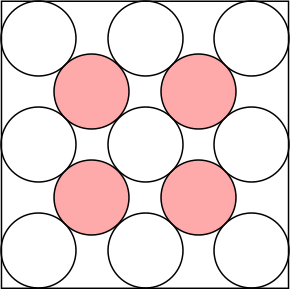

s = 2 + 4 √2 = 7.656+
n=5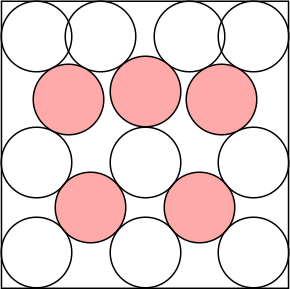

s = 8.131+ 		n=6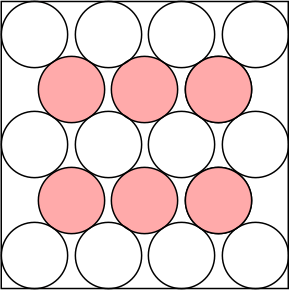

s = 2 + 24/√13 = 8.656+ 		n=7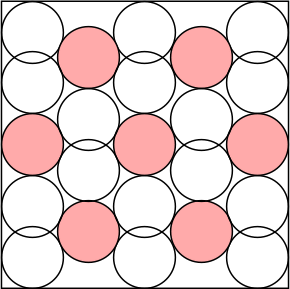

s = 4 + 2√7 = 9.291+ 		n=8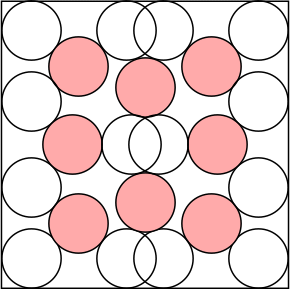

s = 9.683+ 		n=9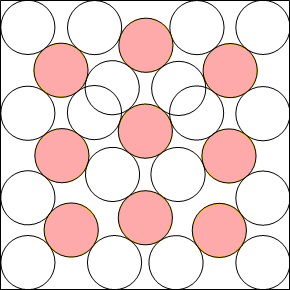

s = 10.671+ (MM)

Placing n Circles So That No More Than 1 More Fits
n=0

s = 2 + √2 = 3.414+ 		n=1

s = 2 + 2 √2 = 4.828+ 		n=2

s = 2 (7 + 4√3)/5 = 5.571+ 		n=3

s = (4 + 3√2 + √30)/2 = 6.859+ 		n=4

s = 2 + 4 √2 = 7.656+
n=5

s = 8.297+ 		n=6

s = 8.893+ (MM) 		n=7

s = 9.425+ (MM) 		n=8

s = 10.223+ 		n=9

s = 10.671+ (MM)

Placing n Circles So That No More Than 2 More Fit
n=0

s = 2 + (√6 + √2)/2 = 3.931+ 		n=1

s = 2 + 12/√13 = 5.328+ 		n=2

s = 2 + 3 √2 = 6.242+ 		n=3

s = 7.284+ (MM) 		n=4

s = 8.058+
n=5

s = 8.570+ 		n=6

s = 9.185+ 		n=7

s = 2 + 3√2 + √14 = 9.984+ 		n=8

s = 10.449+ (MM)

Placing n Circles So That No More Than 3 More Fit
n=0

s = 4 		n=1

s = 5.592+ 		n=2

s = 6.603+ (MM) 		n=3

s = 7.385+ 		n=4

s = 8.297+

Placing n Circles So That No More Than 4 More Fit
n=0

s = 2 + 2√2 = 4.828+ 		n=1

s = 2 + √6 + √2 = 5.863+ 		n=2

s = 7.080+ (MM) 		n=3

s = 2 + 4√2 = 7.656+ 		n=4

s = 3 + √31 = 8.567+

Placing n Circles So That 0 More Fit in a Triangle
n=0

s = 2√3 = 3.464+ (MM) 		n=1

s = 4√3 = 6.928+ (MM) 		n=2

s = 4 + 2√3 = 7.464+ (MM) 		n=3

s = 6√3 = 10.392+ (MM) 		n=4

s = 4 + 4√3 = 10.928+ (MM)

Andrew B. Hudson investigated the problem for squares in circles:

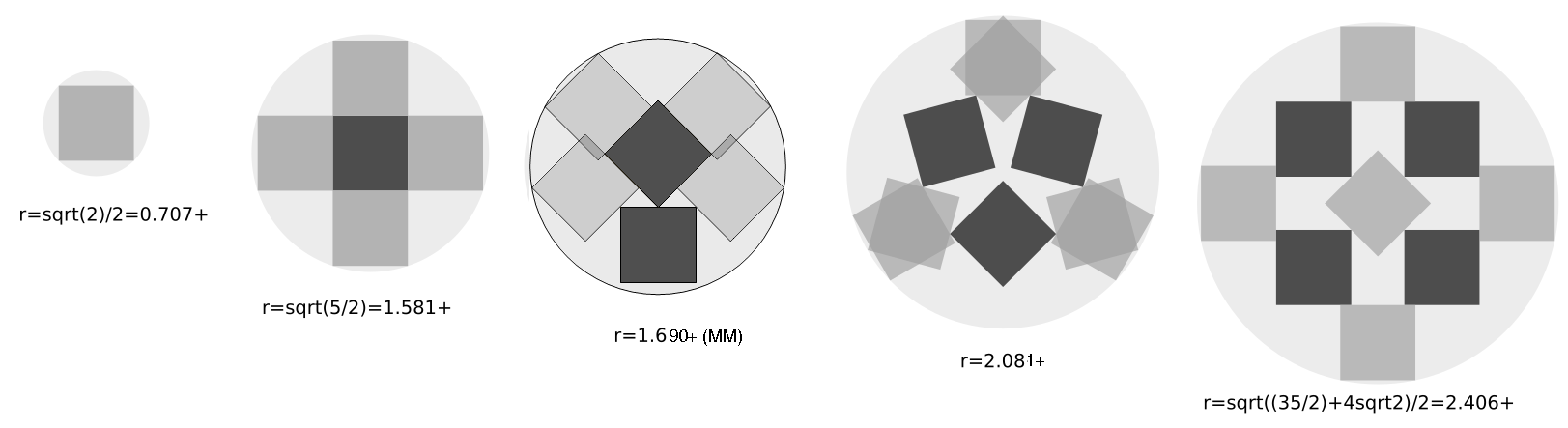
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 1/15/20.