Problem of the Month (February 2007)

This month we investigate chess positions containing two types of pieces A and B subject to the condition: each A attacks exactly n B's (and no A's), and each B attacks exactly m A's (and no B's). Can you find smaller solutions? Can you solve one of the unsolved cases? What are the smallest solutions for other pairs of pieces?

Given a collection of chess pieces, here are more questions we can ask: What is the smallest arrangement so that each piece attacks exactly one piece of each type, including its own? What is the smallest arrangement so that each piece attacks one piece of each other type, not including its own? How about two of each piece? Given a cycle of pieces, what is the smallest arrangement so that each piece attacks only one of the piece next in the cycle? How about two of the next piece?

ANSWERS

Here are the smallest known solutions for 2 pieces A and B (possibly equal) where A attacks exactly n B's (and no A's), and each B attacks exactly m A's (and no B's).

Bishops and Knights

B=1 B=2 B=3 B=4
N=1
N=2 see below
N=3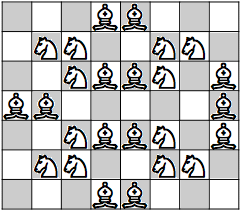
(Johannes Waldmann)
N=4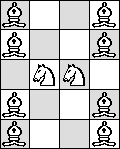

B=3 N=2

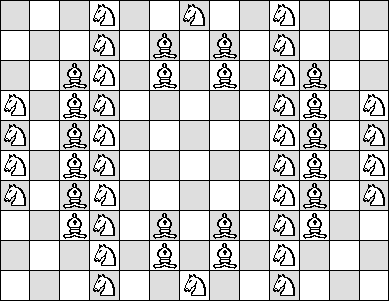
(Maurizio Morandi)

Bishops and Kings

B=1 B=2 B=3 B=4
K=1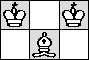
K=2
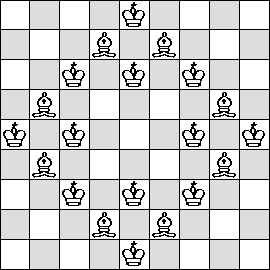K=3
(proved by
Joe DeVincentis)
K=4 ?
K=5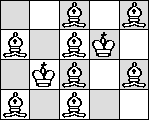

Bishops and Rooks

B=1 B=2 B=3 B=4
R=1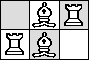
(Maurizio Morandi) 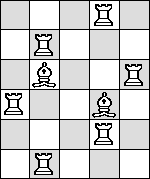see below
R=2
(Maurizio Morandi)
R=3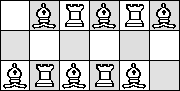
(Maurizio Morandi)
R=4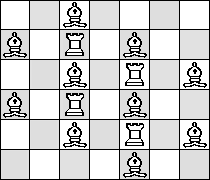
(Maurizio Morandi)

B=4 R=1

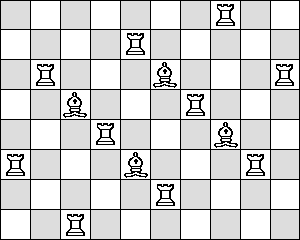
(Maurizio Morandi)

Bishops and Queens

B=1 B=2 B=3 B=4
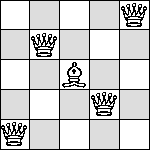
Q=1
Q=2 see below
Q=3
(Maurizio Morandi)
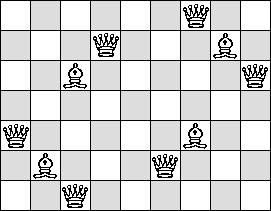
(Maurizio Morandi) see below
Q=4
Q=5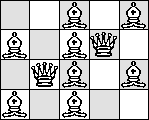
(James Wilson)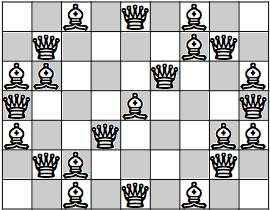
(Johannes Waldmann)
Q=6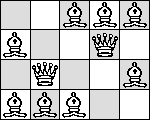
(Maurizio Morandi)
Q=7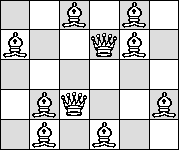
Q=8
(Maurizio Morandi)

B=4 Q=2

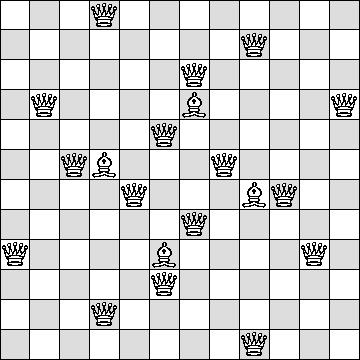
B=4 Q=3

(Maurizio Morandi)

Kings and Knights

K=1 K=2 K=3
N=1
(Johan de Ruiter)
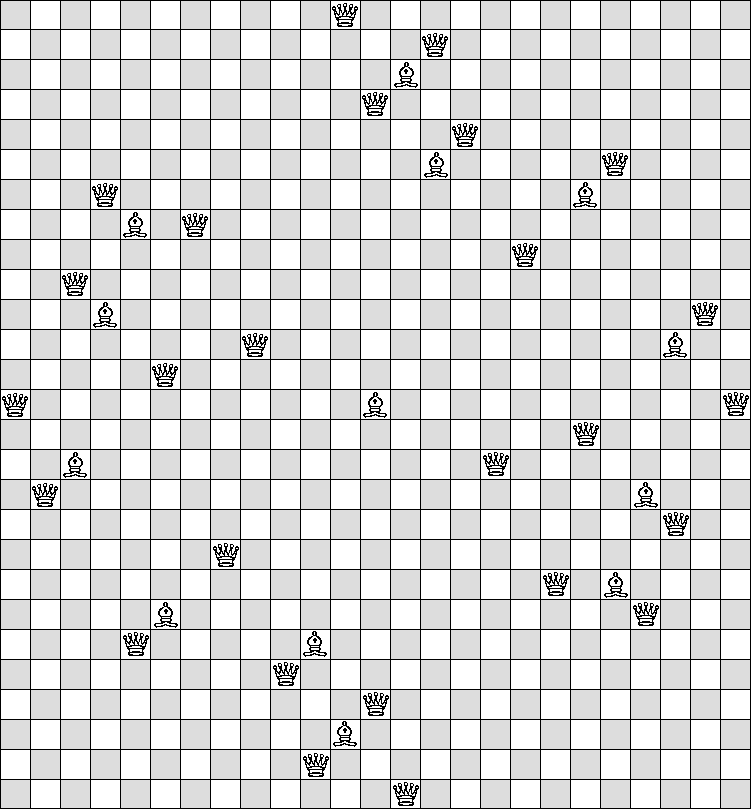
N=2
(James Wilson)
N=3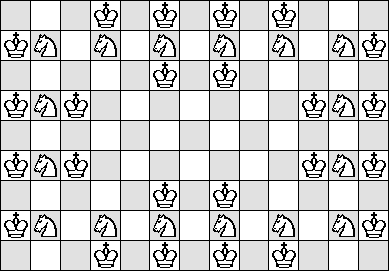
(Maurizio Morandi) ? ?

Kings and Queens

K=1 K=2
Q=1
Q=2
Q=3
Q=4
Q=5 ?
Q=6
(Maurizio Morandi)

Kings and Rooks

K=1 K=2 K=3 K=4
R=1
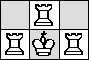R=2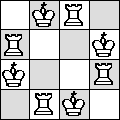
(proved by
Joe DeVincentis)
R=3
(proved by
Joe DeVincentis)

Knights and Rooks

N=1 N=2 N=3 N=4
R=1
(Maurizio Morandi)
(Maurizio Morandi)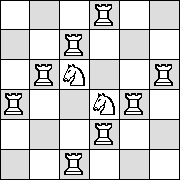
R=2
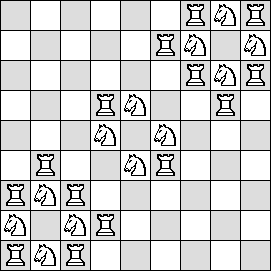
(Maurizio Morandi) ?
R=3
(Maurizio Morandi) ?
R=4
(Maurizio Morandi)

Knights and Queens

N=1 N=2 N=3
Q=1
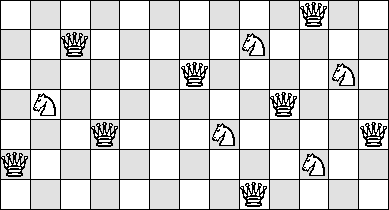
(James Wilson)
Q=2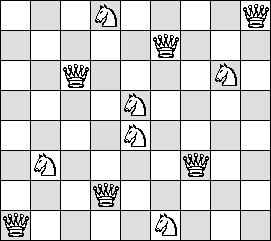
(Maurizio Morandi) see below
Q=3
(Maurizio Morandi) ?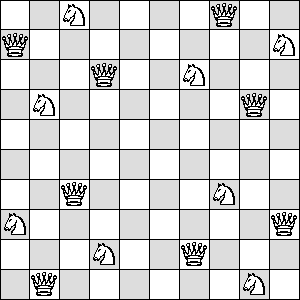
Q=4 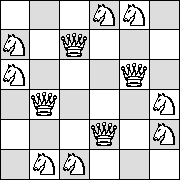see below

N=2 Q=4

N=3 Q=2

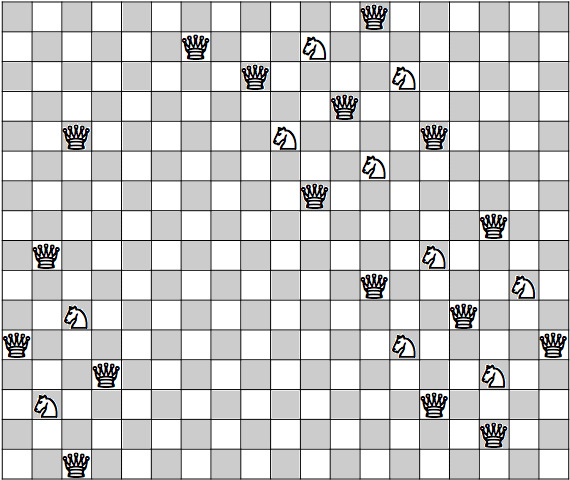
(Johannes Waldmann)

Queens and Rooks

R=1 R=2 R=3 R=4
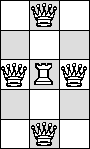
Q=1
Q=2 see below
Q=3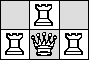
(Maurizio Morandi)
(Maurizio Morandi) see below
Q=4
Q=5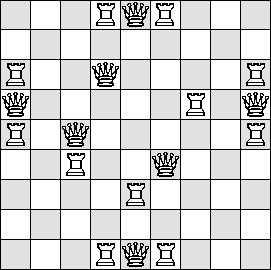
(Maurizio Morandi)
Q=6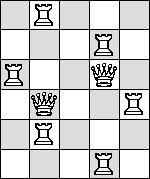
Q=7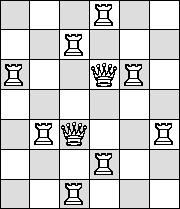
Q=8 see below

Q=2 R=4

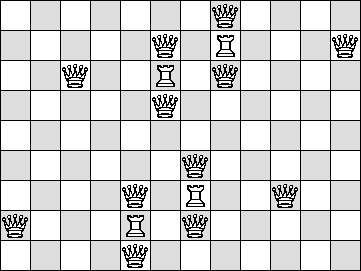
(Maurizio Morandi)
Q=3 R=4

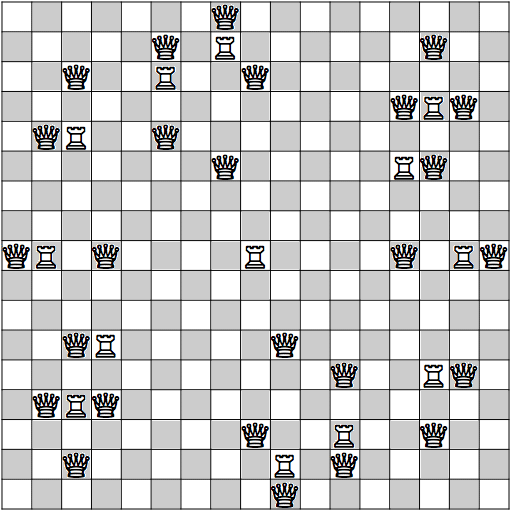
(Johannes Waldmann)
Q=8 R=1

Bishops and Bishops

B=1 B=2
B=1
B=2
B=3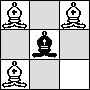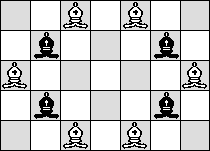
(Maurizio Morandi)

B=4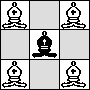

Kings and Kings

K=1 K=2
K=1
K=2
K=3
K=4

Knights and Knights

N=1 N=2 N=3 N=4
N=1
N=2
N=3
N=4
(Johan de Ruiter)
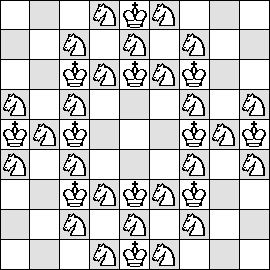
N=5 shown here
(Johannes Waldmann) shown here
(Johannes Waldmann)
N=6 ?
N=7 ?
N=8

Queens and Queens

Q=1 Q=2 Q=3 Q=4
Q=1
Q=2
Q=3
Q=4
Q=5 ? ?
Q=6 ? ?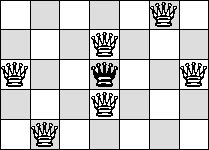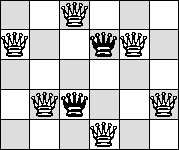
Q=7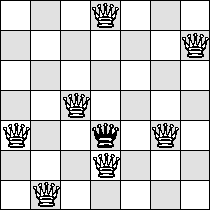
(Maurizio Morandi)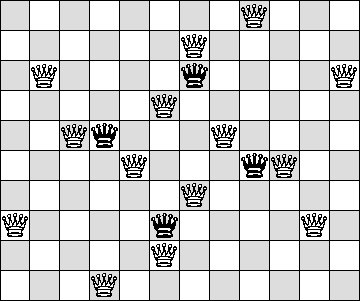
(Maurizio Morandi) ? ?
Q=8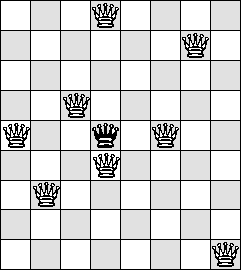
(Maurizio Morandi)
(Maurizio Morandi) ? ?

Rooks and Rooks

R=1 R=2
R=1
R=2
R=3
R=4

Here are the smallest known solutions for collections of pieces (possibly repeated) where each piece attacks exactly 1 of every other type of piece.

2 Pieces

B K N Q R
B
K
N
Q
R

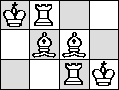
3 Pieces Without Repetition

no B no K no N no Q
no K
no N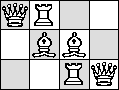
no Q
(Maurizio Morandi)
no R
(Maurizio Morandi)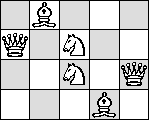
(Maurizio Morandi)
(Maurizio Morandi)

3 Pieces With Repetition

B K N Q R
BB
(Maurizio Morandi)
(Maurizio Morandi)
(Maurizio Morandi)
KK
(Maurizio Morandi)
(Maurizio Morandi)
NN
(Maurizio Morandi)
(Maurizio Morandi)
QQ
(Maurizio Morandi)
RR
(Maurizio Morandi)

4 Pieces All Alike

BBBB
KKKK
NNNN
QQQQ
RRRR

Here are the smallest known solutions for collections of pieces (possibly repeated) where each piece attacks exactly 1 of each type of piece, including its own.

2 Pieces

B K N Q R
B
K
N
(Maurizio Morandi)
Q
(Maurizio Morandi)
R
(Maurizio Morandi)

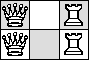3 Pieces Without Repetition

no B no K no N no Q
no K
no N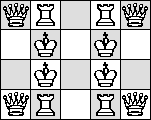
(Maurizio Morandi)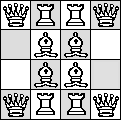
(Maurizio Morandi)
no Q
(Maurizio Morandi)
(Maurizio Morandi)
(Maurizio Morandi)
no R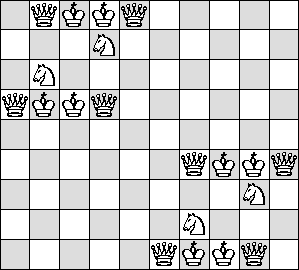
(Maurizio Morandi)

(Maurizio Morandi)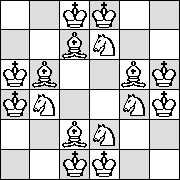
(Maurizio Morandi)

3 Pieces With Repetition

B K N Q R
BB
(Maurizio Morandi)
KK
(Maurizio Morandi)
(James Wilson)
NN
(Maurizio Morandi) 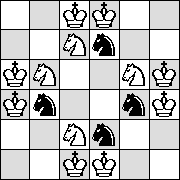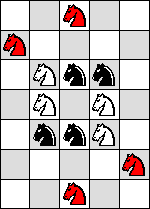see below
QQ
(Maurizio Morandi)
RR ?

NNR

(Maurizio Morandi)

4 Pieces All Alike

BBBB
KKKK
NNNN
QQQQ
RRRR

Here are the smallest known solutions for collections of pieces (possibly equal) where each piece attacks exactly 2 of each type of piece, including its own.

1 Piece

B
K
N
Q
R

2 Pieces

B K N Q R
B
K
(proved by
James Wilson)
(proved by
James Wilson)
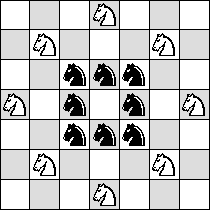
N ? ?
Q
(Maurizio Morandi)
R ?

Here are the smallest known solutions for cycles of 3 or more pieces where each piece attacks exactly 1 piece of the next type in the cycle (and no others of any type).

3 Pieces Without Repetition

B → K → N →
B → K → R →
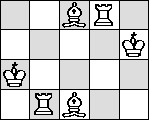
B → N → K →
B → N → R →

B → R → K →
B → R → N →
K → N → R →
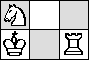
K → R → N →

N → Q → B →
N → Q → K →
N → Q → R →

4 Pieces Without Repetition

B → K → N → R →
B → K → R → N →
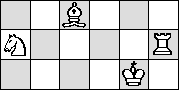
B → N → K → R →

(Johan de Ruiter) B → N → R → K →

(Johan de Ruiter)

B → R → K → N →
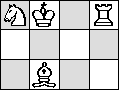
B → R → N → K →
N → Q → B → K →
N → Q → B → R →

N → Q → K → B →
N → Q → K → R →
N → Q → R → B →
N → Q → R → K →

4 Pieces With Repetition

B → K → B → K →
B → K → B → N →
B → K → B → R →
B → N → B → N →

B → N → B → R →
B → R → B → R →
K → B → K → N →
K → B → K → R →

K → N → K → N →
K → N → K → R →
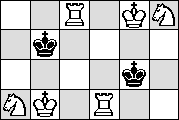
K → R → K → R →

N → B → N → K →
N → B → N → R →
N → K → N → R →

(Maurizio Morandi) N → R → N → R →

N → Q → N → B →

(Maurizio Morandi) N → Q → N → K →
N → Q → N → R →
N → Q → N → Q →

R → B → R → K →
R → B → R → N →
R → K → R → N →

(Maurizio Morandi)

5 Pieces Without Repetition

N → Q → B → K → R →
N → Q → B → R → K →

(Johan de Ruiter) N → Q → K → B → R →

(Johan de Ruiter)

N → Q → K → R → B →
N → Q → R → B → K →
N → Q → R → K → B →

(Johan de Ruiter)

Here are the smallest known solutions for cycles of 3 or more pieces where each piece attacks exactly 2 pieces of the next type in the cycle (and no others of any type).

3 Pieces Without Repetition

B → K → N →
B → K → R →
? B → N → K →

(Maurizio Morandi) B → N → R →

B → R → K →
? B → R → N →
K → N → R →
? K → R → N →
N → Q → B →

N → Q → K →

(Maurizio Morandi) N → Q → R →

4 Pieces Without Repetition

B → K → N → R →
? B → K → R → N →
? B → N → K → R →
?

B → N → R → K →
? B → R → K → N →
? B → R → N → K →
?

N → Q → B → K →
? N → Q → B → R →

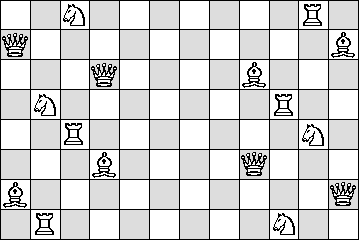
N → Q → K → B →
? N → Q → K → R →
? N → Q → R → K →
?

N → Q → R → B →

(Maurizio Morandi)

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 7/2/23.