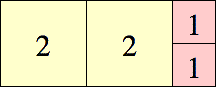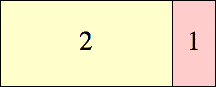Problem of the Month (February 2012)
We call a tiling of integer squares an ascending tiling if the number of squares of side n is non-decreasing in n (up to the maximum n involved in the tiling). We call a tiling a (a,b) ascending tiling if it contains only squares with sides between a and b, with at least one square of each side. We call such a tiling minimal if it has the smallest area of such a tiling. What are the minimum (a,b) tilings of rectangles? What about minimum (a,b) tilings of squares? Equilateral triangles with smaller equilateral triangles? Other small polyominoes or polyiamonds?
ANSWERS
George Sicherman noted that the first 6 tilings could have bi-rotary symmetry. And he showed that there are solutions for all cases.
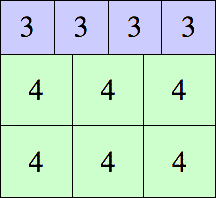
Jeremy Galvagni showed that the minimal (n,n+1) rectangle tiling is (3n+2) × n(n+1), and the minimal (n,n+1) square tiling is n(n+2) × n(n+2) for large n.
Bryce Herdt sent some domino tilings.
Brian Trial found and improved many of the largest best-known tilings.
Smallest Known Ascending Tilings of Squares in Rectangles
| b \ a | 1 | 2 | 3 | 4 | 5
| 2
| 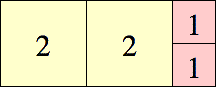
2 × 5
|
|---|
| 3
| 
7 × 8
| 
6 × 8
|
|---|
| 4
| 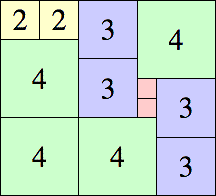
10 × 11
| 
8 × 14
| 
11 × 12
|
|---|
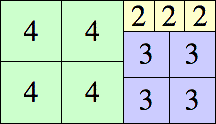
| 5
| 
10 × 21
| 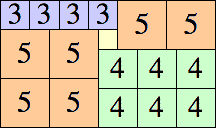
13 × 22
| 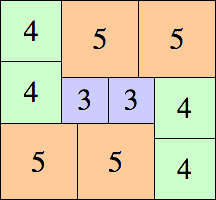
13 × 14
| 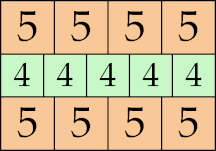
14 × 20
|
|---|
| 6
| 
11 × 22
| 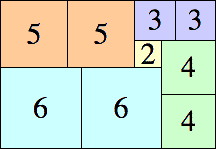
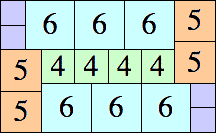
11 × 16
| 
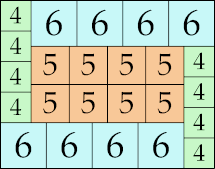
16 × 26
| 
22 × 28 (GS)
| 
17 × 30
|
|---|
| 7
| 
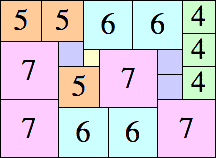
18 × 25
| 
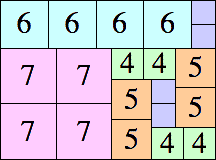
19 × 26
| 
20 × 27
| 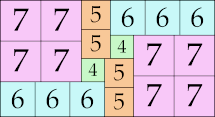
20 × 37 (GS)
| 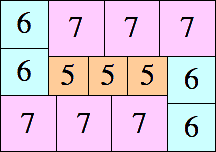
19 × 27
|
|---|
| 8
| 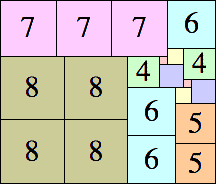
23 × 27
| 
26 × 29
| 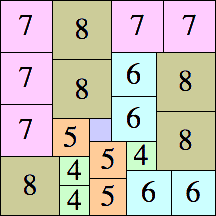
29 × 29
| 
22 × 56 (GS)
| 
37 × 38 (GS)
|
|---|
| 9
| 
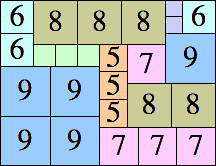
25 × 32
| 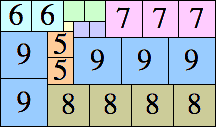
24 × 41
| 
30 × 39
| 
26 × 60 (GS)
| 
34 × 48 (GS)
|
|---|
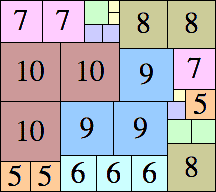
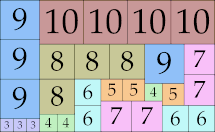
| 10
| 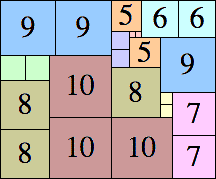
29 × 35
| 
32 × 36
| 
30 × 49 (GS)
| 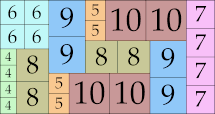
28 × 53 (GS)
| 
40 × 53 (GS)
|
|---|
| 11
| 
31 × 48 (GS)
| 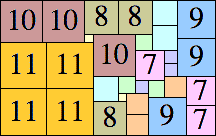
32 × 51 (BT)
| 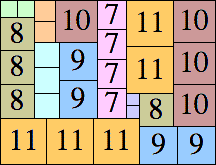
39 × 51 (BT)
| 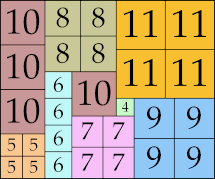
40 × 48 (GS)
| 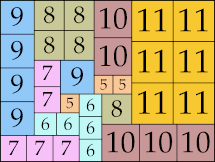
43 × 57 (GS)
|
|---|
| 12
| 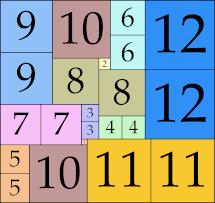
35 × 37 (GS)
| 
27 × 67 (BT)
| 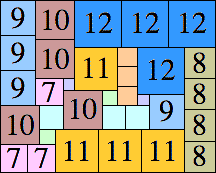
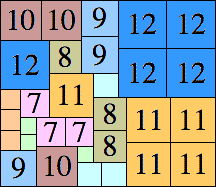
44 × 55 (BT)
| 
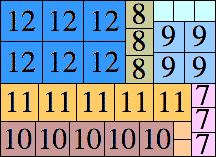
46 × 53 (BT)
| 
45 × 62 (BT)
|
|---|
| 13
| 
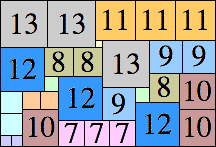
37 × 56 (BT)
| 
40 × 59 (BT)
| 
44 × 59 (BT)
| 
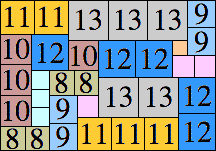
44 × 69 (BT)
| 
49 × 70 (BT)
|
|---|
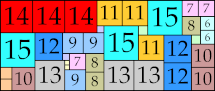
| 14
| 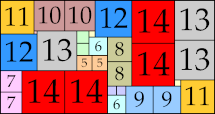
37 × 70 (BT)
| 
46 × 63 (BT)
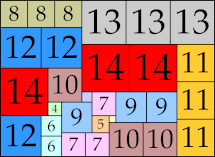
| 
57 × 63 (BT)
| 
61 × 62 (BT)
| 
40 × 93 (GS)
|
|---|
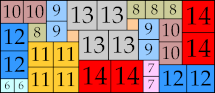
| 15
| 
40 × 62 (BT)
| 
39 × 93 (BT)
| 
48 × 77 (BT)
| 
37 × 118 (BT)
| 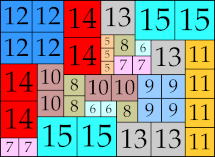
59 × 81 (BT)
|
|---|
| 16
| 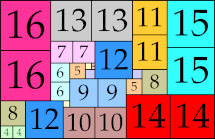
44 × 68 (BT)
| ?
| ?
| ?
| ?
|
|---|
|
Smallest Known Ascending Tilings of Squares in Squares
| b \ a | 1 | 2 | 3 | 4 | 5
| 2
| 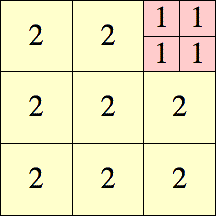
6 × 6
|
|---|
| 3
| 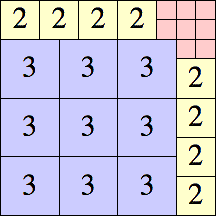
11 × 11
| 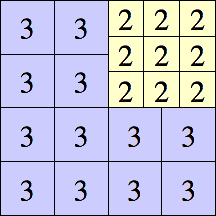
12 × 12
|
|---|
| 4
| 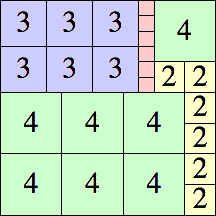
14 × 14
| 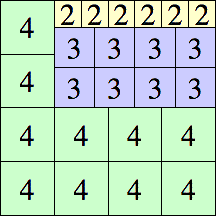
16 × 16
| 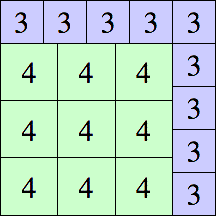
15 × 15
|
|---|
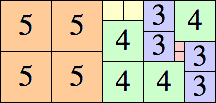
| 5
| 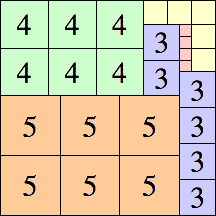
18 × 18
| 
18 × 18 (GS)
| 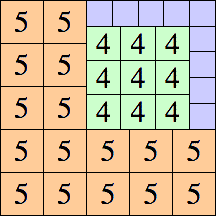
25 × 25
| 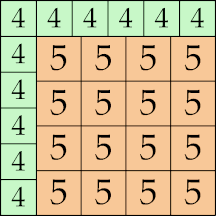
24 × 24
|
|---|
| 6
| 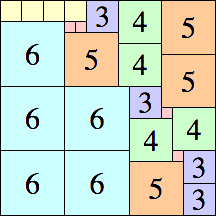
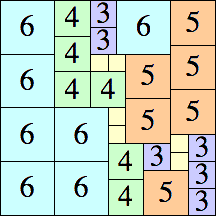
20 × 20
| 
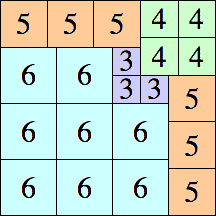
24 × 24
| 
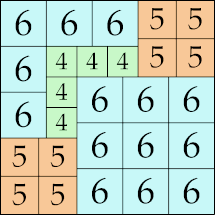
23 × 23
| 
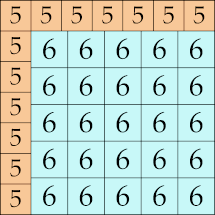
28 × 28 (GS)
| 
35 × 35
|
|---|
| 7
| 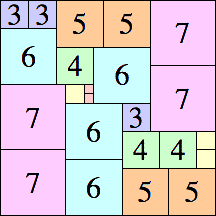
23 × 23
| 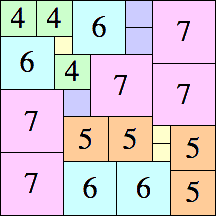
24 × 24
| 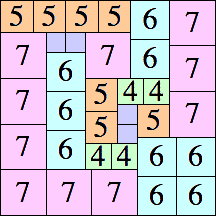
33 × 33
| 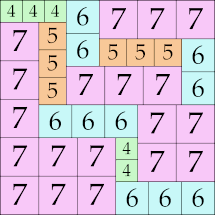
39 × 39 (GS)
| 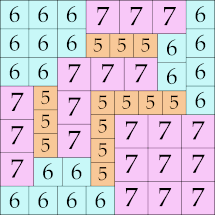
45 × 45 (GS)
|
|---|
| 8
| 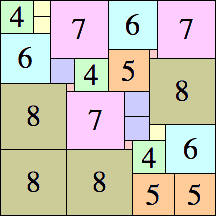
26 × 26
| 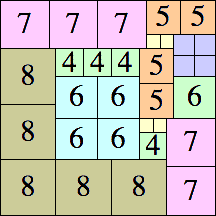
31 × 31
| 
29 × 29
| 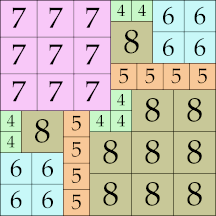
41 × 41 (GS)
| 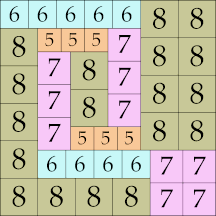
46 × 46 (GS)
|
|---|
| 9
| 
31 × 31
| 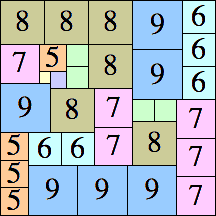
39 × 39 (BT)
| 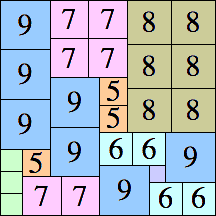
39 × 39 (BT)
| 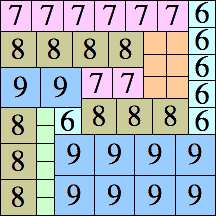
48 × 48 (BT)
| 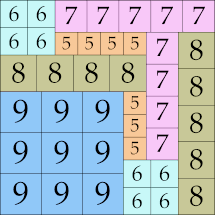
47 × 47 (GS)
|
|---|
| 10
| 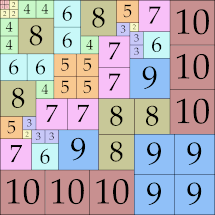
48 × 48
| 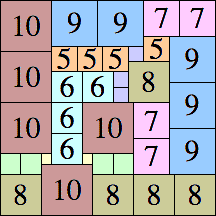
42 × 42 (BT)
| 
45 × 45 (BT)
| 
55 × 55 (GS)
| 
47 × 47 (GS)
|
|---|
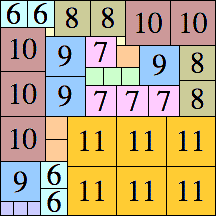
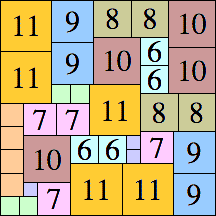
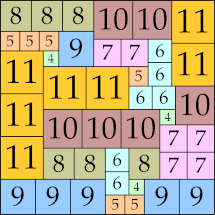
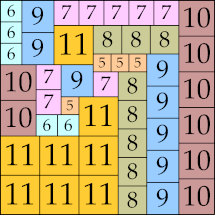
| 11
| 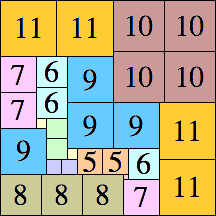
42 × 42 (BT)
| 
48 × 48 (BT)
| 
46 × 46 (BT)
| 
55 × 55 (BT)
| 
60 × 60 (BT)
|
|---|
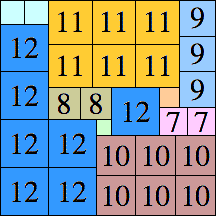
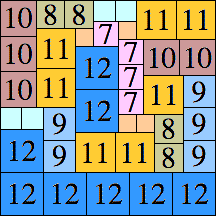
| 12
| 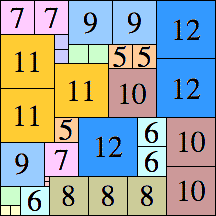
44 × 44 (BT)
| 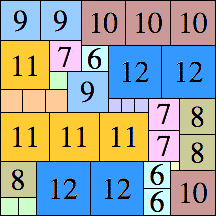
48 × 48 (BT)
| 
53 × 53 (BT)
| 
54 × 54 (BT)
| 
60 × 60 (BT)
|
|---|
| 13
| 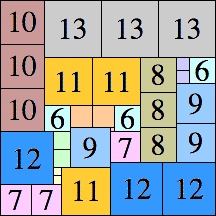
49 × 49 (BT)
| 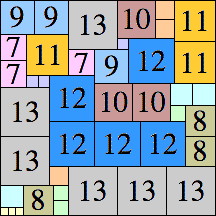
57 × 57 (BT)
| 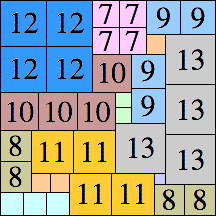
56 × 56 (BT)
| 
60 × 60 (BT)
| 
61 × 61 (BT)
|
|---|
| 14
| 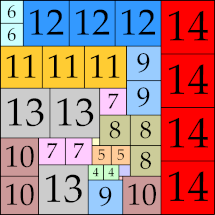
56 × 56 (BT)
| 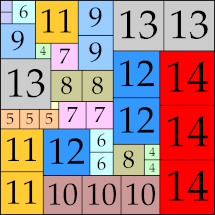
55 × 55 (BT)
| ?
| ?
| ?
|
|---|
|
George Sicherman showed that there are solutions for all the triangular cases as well.
Smallest Known Ascending Tilings of Triangles
| b \ a | 1 | 2 | 3 | 4 | 5
| 2
| 
6
|
|---|
| 3
| 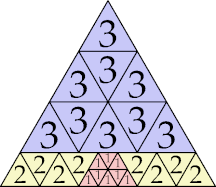
11 (GS)
| 
12 (GS)
|
|---|
| 4
| 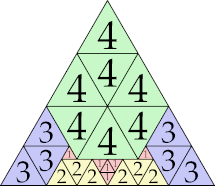
14 (GS)
| 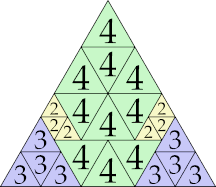
16 (GS)
| 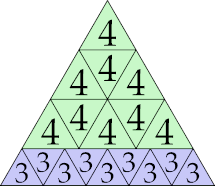
15 (GS)
|
|---|
| 5
| 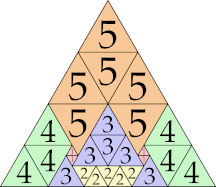
18 (GS)
| 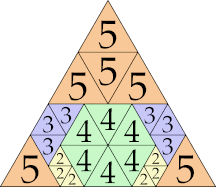
18 (GS)
| 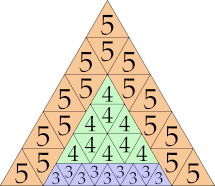
25 (GS)
| 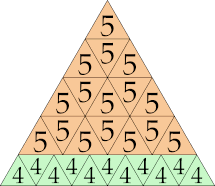
24 (GS)
|
|---|
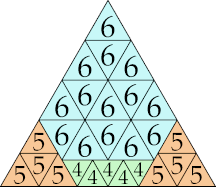
| 6
| 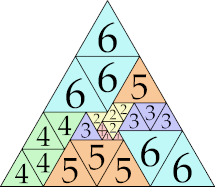
20 (GS)
| 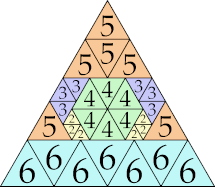
24 (GS)
| 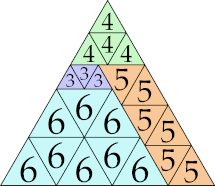
23 (GS)
| 
28 (GS)
| 
35 (GS)
|
|---|
| 7
| 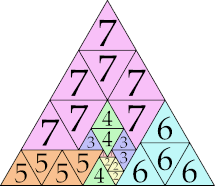
26 (GS)
| 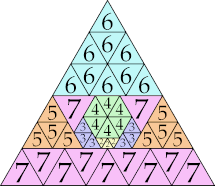
35 (GS)
| 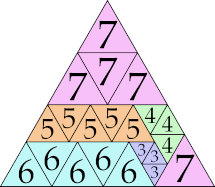
25 (GS)
| 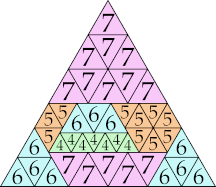
38 (GS)
| 
45 (GS)
|
|---|
| 8
| 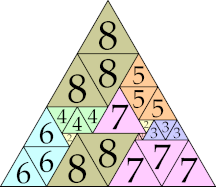
28 (GS)
| 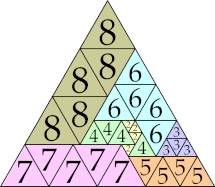
31 (GS)
| 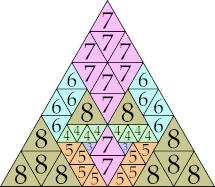
42 (GS)
| 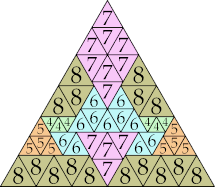
48 (GS)
| 
56 (GS)
|
|---|
|
Smallest Known Ascending Tilings of Dominoes in Rectangles
| b \ a | 1 | 2 | 3 | 4 | 5
| 2
| 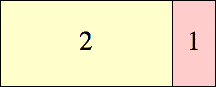
2 × 5
|
|---|
| 3
| 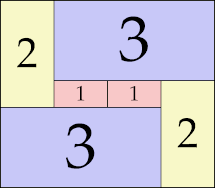
7 × 8 (GS)
| 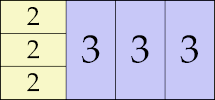
6 × 13 (GS)
|
|---|
| 4
| 
10 × 11 (GS)
| 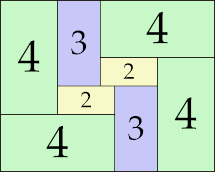
12 × 15 (GS)
| 
11 × 12 (BH)
|
|---|
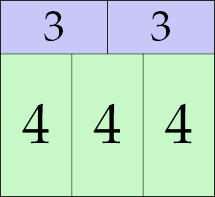
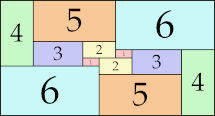
| 5
| 
10 × 21 (GS)
| 
14 × 23 (GS)
| 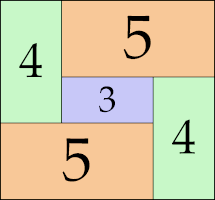
13 × 14 (GS)
| 
20 × 23 (GS)
|
|---|
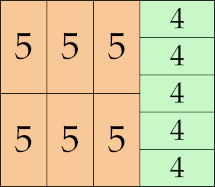
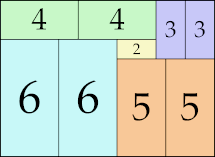
| 6
| 
14 × 26 (GS)
| 
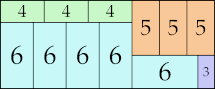
16 × 22 (GS)
| 
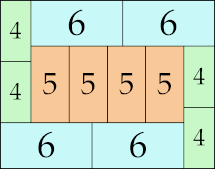
16 × 39 (GS)
| 
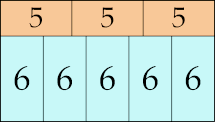
22 × 28 (GS)
| 
17 × 30 (GS)
|
|---|
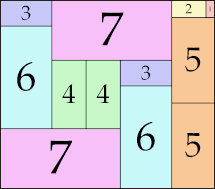
| 7
| 
22 × 25 (GS)
| 
19 × 34 (GS)
| 
20 × 27 (GS)
| 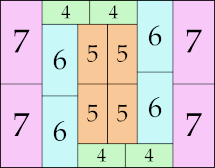
28 × 36 (GS)
| 
27 × 38 (GS)
|
|---|
| 8
| 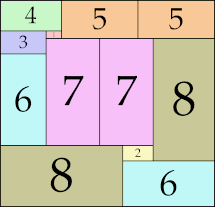
27 × 28 (GS)
| 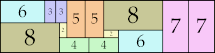
14 × 58 (GS)
| 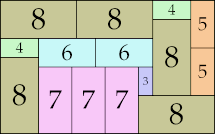
28 × 45 (GS)
| 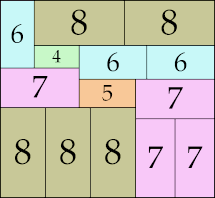
35 × 38 (GS)
| 
38 × 51 (GS)
|
|---|
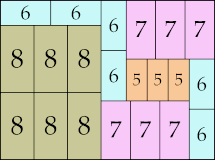
| 9
| 
32 × 35 (GS)
| 
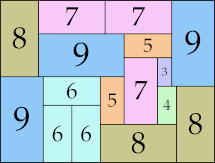
24 × 47 (GS)
| 
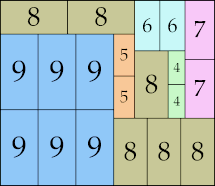
34 × 45 (GS)
| 
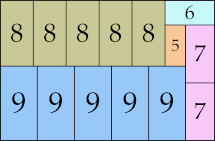
38 × 53 (BT)
| 
34 × 52 (GS)
|
|---|
| 10
| 
36 × 42 (GS)
| 
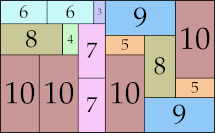
32 × 48 (GS)
| 
34 × 55 (GS)
| 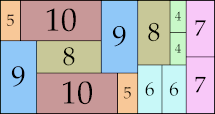
28 × 53 (GS)
| 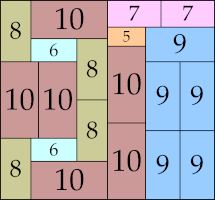
52 × 56 (GS)
|
|---|
| 11
| 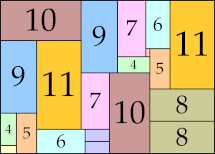
38 × 53 (BT)
| 
38 × 58 (BT)
| 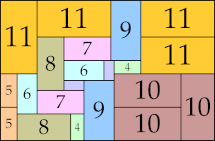
42 × 64 (BT)
| 
46 × 62 (BT)
| 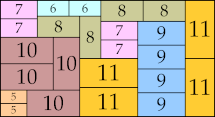
44 × 81 (BT)
|
|---|
| 12
| 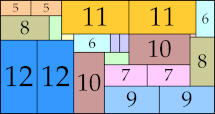
37 × 70 (GS)
| 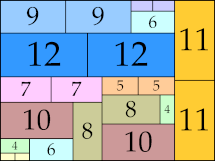
44 × 59 (BT)
| 
42 × 82 (BT)
| 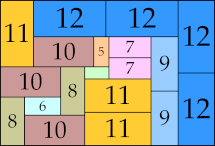
48 × 71 (BT)
| 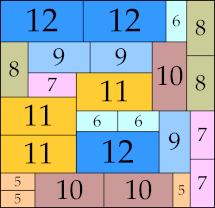
60 × 62 (BT)
|
|---|
| 13
| 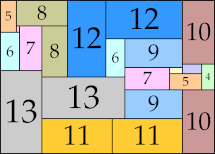
48 × 67 (BT)
| 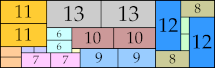
32 × 102 (BT)
| 
44 × 74 (BT)
| 
62 × 76 (BT)
| 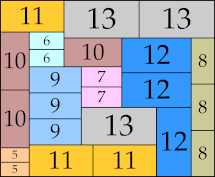
61 × 74 (BT)
|
|---|
| 14
| 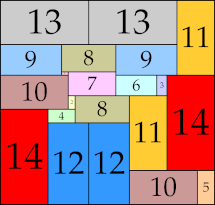
60 × 63 (GS)
| 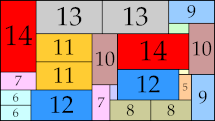
47 × 84 (BT)
| 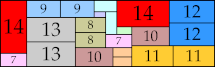
35 × 114 (BT)
| 
58 × 82 (BT)
| 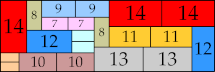
38 × 114 (GS)
|
|---|
|
If you can extend any of these results, please
e-mail me.
Click here to go back to Math Magic. Last updated 2/10/12.