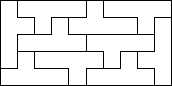
 will pack is the 10×5 rectangle shown below:
will pack is the 10×5 rectangle shown below:

We consider one dimensional disconnected polyominoes, collections of lattice squares in a line. We ask which can tile rectangles, and how many polyominoes are needed. The smallest number of polyominoes that tiles some rectangle is called the order of the polyomino.
Some of these are easy, as they will tile an n×1 rectangle for some n. For example, the polyomino  tiles a 6×1 rectangle. Others are more difficult, like
tiles a 6×1 rectangle. Others are more difficult, like  , which tiles a 15×12 rectangle. Others, like
, which tiles a 15×12 rectangle. Others, like  , cannot tile a rectangle at all.
, cannot tile a rectangle at all.
So which polyominoes can tile a rectangle? Of these, what is the order?
I wondered whether increasing the rectangle to 3 (or more!) dimensions would help polyominoes tile. I conjectured that all polyominoes tile some d-dimensional cube. Reid came up with this counterexample, which can obviously never tile the corner of any cube: 
Patrick Hamlyn wrote a computer program that found many minimal tilings, and the number of tilings for various sizes of rectangles.
Joe DeVincentis found some minimal tilings, and he did all his tilings by hand! He notes that in every minimal tiling, the longer dimension is divisible by the number of squares in the polyomino. He asks whether this is true in general. In fact, he challenges anyone to find a tiling of a 1-dimensional polyomino in which the area divides neither dimension of the tiled rectangle. Reid has managed to show that such a polyomino must have area at least 6.
Aaron Meyerowitz has written several papers on tiling disconnected polyominoes in 1 dimension. He told me that Andrew Adler and F. C. Holroyd proved in 1981 that any 1 dimensional triomino tiles some nx1 rectangle. This was also known to Klarner much earlier. He also told me that it follows from one of his papers that the order of such a triomino is the 1 dimensional order. It is not known whether this is true for other polyominoes which tile in 1 dimension.
Meyerowitz also told me that Don Coppersmith proved in 1985 that every tetromino (not necessarily 1 dimensional) tiles the plane. There is a hexomino that does not tile the plane: 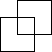 . It is not known whether every pentomino tiles the plane.
. It is not known whether every pentomino tiles the plane.
Meyerowitz also asks 2 questions: "If a polyomino tiles a half strip, must it tile some rectangle?" and "If a polyomino tiles the half line, must it tile a finite interval?"
Rick Eason sent me a detailed description of the packable boxes of  .
.
Here are the results for small length polyominoes:
| Polyomino | Order | Dimensions | Finder | Prover |
|---|---|---|---|---|
 | 2 | 4x1 | ||
 | 2 | 6x1 | ||
 | 3 | 6x1 | ||
 | 2 | 8x1 | ||
 | none | Juha Saukkola | ||
 | 2 | 6x1 | ||
 | 2 | 6x1 | ||
 | 4 | 8x1 |
| Polyomino | Order | Dimensions | Finder | Prover |
|---|---|---|---|---|
 | 2 | 10x1 | ||
 | 24 | 20x6 | Erich Friedman | Patrick Hamlyn |
 | 24 | 16x6 | Joe Devincentis | Patrick Hamlyn |
 | 2 | 8x1 | ||
 | 21 | 12x7 | Erich Friedman | Erich Friedman |
 | 2 | 8x1 | ||
 | 3 | 9x1 | ||
 | 6 | 18x1 | ||
 | 5 | 10x1 |
| Polyomino | Order | Dimensions | Finder | Prover |
|---|---|---|---|---|
 | 2 | 12x1 | ||
 | none | Mike Reid | ||
 | none | Erich Friedman | ||
 | 36 | 15x12 | Patrick Hamlyn | Patrick Hamlyn |
 | 2 | 10x1 | ||
 | 36 | 15x12 | Juha Saukkola | Patrick Hamlyn |
 | none | Erich Friedman | ||
 | 2 | 10x1 | ||
 | none | Erich Friedman | ||
 | 2 | 8x1 | ||
 | 2 | 8x1 | ||
 | 2 | 8x1 | ||
 | 60 | 24x10 | Patrick Hamlyn | Patrick Hamlyn |
 | 2 | 8x1 | ||
 | none | Mike Reid | ||
 | 4 | 12x1 | ||
 | 4 | 12x1 | ||
 | 3 | 9x1 | ||
 | 6 | 12x1 |
| Polyomino | Order | Dimensions | Finder | Prover |
|---|---|---|---|---|
 | 2 | 14x1 | ||
 | none | Mike Reid | ||
 | none | Mike Reid | ||
 | 70 | 30x14 | Mike, Patrick | Patrick Hamlyn |
 | 2 | 12x1 | ||
 | none | Mike Reid | ||
 | 32 | 24x8 | Mike, Erich | Patrick Hamlyn |
 | none | Erich Friedman | ||
 | 2 | 12x1 | ||
 | none | Mike Reid | ||
 | none | Erich Friedman | ||
 | none | Erich Friedman | ||
 | 48 | 30x8 | Mike, Joe | Patrick Hamlyn |
 | 78 | 30x13 | Mike, Patrick | Patrick Hamlyn |
 | 2 | 10x1 | ||
 | 90 | 50x9 | Mike, Joe | Patrick Hamlyn |
 | none | Mike Reid | ||
 | 2 | 10x1 | ||
 | 45 | 25x9 | Mike, Joe | Patrick Hamlyn |
 | 96 | 60x8 | Mike, Patrick | Patrick Hamlyn |
 | 2 | 10x1 | ||
 | 2 | 10x1 | ||
 | 3 | 12x1 | ||
 | 84 | 28x12 | Mike, Patrick | Patrick Hamlyn |
 | 8 | 32x1 | ||
 | 66 | 24x11 | Mike, Patrick | Patrick Hamlyn |
 | 3 | 12x1 | ||
 | 240? | 20x48 | Mike Reid | |
 | 6 | 24x1 | ||
 | 50 | 20x10 | Mike, Joe | Patrick Hamlyn |
 | 102 | 24x17 | Mike, Patrick | Patrick Hamlyn |
 | 4 | 12x1 | ||
 | 10 | 30x1 | ||
 | 12 | 36x1 | ||
 | 7 | 14x1 |
| Polyomino | Order | Dimensions | Finder | Prover |
|---|---|---|---|---|
 | 2 | 16x1 | ||

| none | Mike Reid | ||

| none | Mike Reid | ||

| none | Mike Reid | ||
 | 54 | 42x9 | Patrick Hamlyn | Patrick Hamlyn |

| 2 | 14x1 | ||

| none | Mike Reid | ||
 | 36 | 28x9 | Patrick Hamlyn | Patrick Hamlyn |

| none | Patrick Hamlyn | ||

| none | Erich Friedman | ||

| 2 | 14x1 | ||

| none | Mike Reid | ||

| none | Mike Reid | ||

| none | Mike Reid | ||

| none | Mike Reid | ||

| none | Mike Reid | ||

| ? | |||

| ? | |||

| 2 | 12x1 | ||
 | 30 | 18x10 | Patrick Hamlyn | Patrick Hamlyn |

| none | Mike Reid | ||

| none | Mike Reid | ||

| 2 | 12x1 | ||

| none | Mike Reid | ||

| 180? | 108x10 | Mike, Patrick | |

| none | Mike Reid | ||

| none | Mike Reid | ||

| none | Mike Reid | ||

| 36 | 24x9 | Mike, Patrick | Patrick Hamlyn |

| ? | |||

| none | Mike Reid | ||

| none | Mike Reid | ||

| 2 | 12x1 | ||

| none | Mike Reid | ||

| 2 | 12x1 | ||
| 2 | 10x1 | ||

| 2 | 10x1 | ||

| ? | |||

| 2 | 10x1 | ||

| 156? | 60x13 | Mike Reid | |

| 2 | 10x1 | ||

| 2 | 10x1 | ||

| 2 | 10x1 | ||

| 234? | 90x13 | Mike Reid | |

| none | Mike Reid | ||

| 72 | 30x12 | Mike, Patrick | Mike Reid |

| 108 | 45x12 | Mike, Patrick | Patrick Hamlyn |

| 2 | 10x1 | ||

| 240? | 100x12 | Mike Reid | |

| 2 | 10x1 | ||

| ? | |||

| 48 | 20x12 | Patrick Hamlyn | Patrick Hamlyn |

| none | Mike Reid | ||

| ? | |||

| 4 | 16x1 | ||
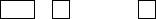
| 88 | 32x11 | Mike Reid | Patrick Hamlyn |

| 4 | 16x1 | ||
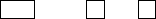
| 48 | 16x12 | Patrick Hamlyn | Patrick Hamlyn |

| 120? | 40x12 | Patrick Hamlyn | |

| ? | |||
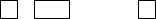
| 60 | 24x10 | Mike Reid | Mike Reid |

| 4 | 16x1 | ||
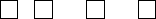
| 6 | 24x1 | ||

| none | Mike Reid | ||

| 60 | 20x12 | Patrick Hamlyn | Patrick Hamlyn |

| ? | |||

| 5 | 15x1 | ||

| 4 | 12x1 | ||

| 4 | 12x1 | ||

| 4 | 12x1 | ||

| 8 | 16x1 |
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 3/3/99.