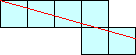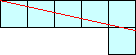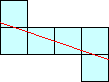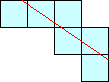Problem of the Month (March 2001)

Polyominoes have been well studied. This month we are concerned with linear polyominoes, those polyominoes with the property that a line can be drawn that intersects the interior of every square in the polyomino. For example, there are 8 linear hexominoes:

Notice that the top three polyominoes are special since a line between two of the corners of the polyomino intersects every square, and the bottom 5 polyominoes are not special. How many linear n-ominoes are there? How many are special? What about in higher dimensions? What is the smallest value of n for which the linear n-ominoes pack into into a rectangle? How about linear polyhexes and polyiamonds?

ANSWERS

Joseph DeVincentis, Trevor Green, and Philippe Fondanaiche found that the number of special linear n-ominoes is equal to the number of relatively-prime non-ordered pairs of positive integers that add to n+1, namely φ(n+1)/2, where φ is Euler's totient function. They note that this is sequence A023022 of the Encyclopedia of Integer Sequences.

Here is the number of linear n-ominoes, furnished by Joseph DeVincentis and Philippe Fondanaiche:

Number of Linear n-ominoes

n	1	2	3	4	5	6	7	8	9	10	11	12
LP(n)	1	1	2	3	5	8	11	17	22	31	38	52

Trevor Green defines a linear polyomino to be semi-special if its line can be drawn through one of the corners of the polyomino. He then notes that almost all semi-special linear polyominoes correspond to rational numbers of the form a/b, with a+b≤n, a≤b and gcd(a,b)=1. The correspondence is that the slopes of the lines is a/b–ε, for some small ε. Unfortunately, some pairs of rational numbers yield rotations of the same linear polyomino when n≤7.

In 2012, Trevor Green found the following formula that counts semi-special linear n-ominoes:

S(n) = 1 + 1/2 [φ(3) + φ(4) + ... + φ(n+1)] –

n/2

Mike Reid thinks he can show that the only sets of linear n-ominoes that can tile a rectangle are the trivial sets n=1 and n=2.

Joseph DeVincentis found that in higher dimensions, the projections of any linear polyomino are linear polyominoes, and the projections of a special linear polyomino are special linear polyominoes. As a result, all of the dimensions of the box must be pairwise relatively prime. The smallest nontrivial one of these is the one inside the 2×3×5 box.

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 10/24/12.