Problem of the Month (March 2004)

This month's problem was stolen from mathpuzzle.com. Jonathan Welton first considered the puzzle of Thunderball, in which there are balls which roll about on the surface of a square grid. By tilting the grid, we can make all the balls move horizontally or vertically the same number of spaces. Balls that would be tilted into a square that has been previously visited remain stationary instead. The object of the puzzle is to get all the balls to consecutive horizontal squares. For example, if the balls start in diagonally adjacent squares, there is a 14 move solution found by Jens Lund: E-E-N-N-W-S-N-N-N-W-S-N-N-E

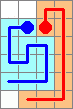
What is the shortest solution for two balls starting in vertically adjacent squares? What about other starting positions? The case of 3 balls starting in diagonally adjacent squares has a solution of length 70. Can you find it? Is there a shorter solution? Can you show that 3 balls can always be solved regardless of the starting position? Can you solve the case of 4 balls starting in diagonally adjacent squares? Do these solutions generalize to larger numbers of balls?

ANSWERS

Clinton Weaver found a 21 move solution for two balls starting vertically adjacent: 2N-2E-S-3W-5N-4E-3S-W

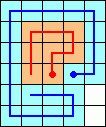
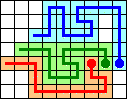
Claudio Baiocchi found the following 15-move solution: E-N-W-N-2E-N-W-2N-E-S-3N

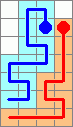
Ed Pegg published this 70-move solution to the case for 3 balls starting diagonally: W-3S-4E-N-E-2S-2W-2S-2W-S-W-3S-6E-6N-S-3W-5S-3N-W-S-9E-11N-W

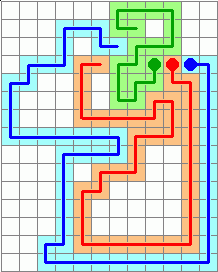
Clint Weaver improved this to a 49-move solution: S-W-6N-8E-S-4W-2S-E-4N-W-E-S-E-3W-4E-6N-4W

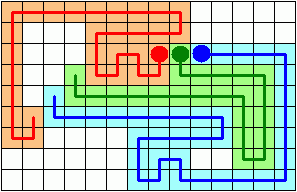
Then Jonathan Welton improved this further to a 47-move solution: S-W-6N-6E-S-5W-S-E-3N-4W-2E-S-5E-6N-4W

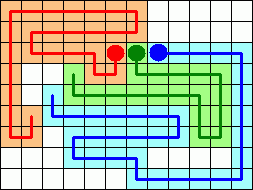
Bill Clagett improved this to a 23-move solution: E-2N-E-2S-2E-N-W-3E-N-W-3E-S-N-3S.

Bill Clagett also found the shortest solutions for the two ball problem starting from any two starting positions. Below is a sample of his data. If the balls start at (0,0) and (x,y), and |x|+|y|>3, then the smallest number of moves it takes to make the balls horizontal is 2|x|+2|y|+1, unless x=0 (in which case the answer is |y|+6) or |y|<2 (in which case the answer is 2|x|–2|y|+7).

starting        solution                    
positions       length     solution         
(0, 0), (0, 1)    15       ENWNEENWNNESNNN  
(0, 0), (0, 2)    13       EENNNWWSESWNN    
(0, 0), (0, 3)    12       NEENNWWSWSSS     
(0, 0), (0, 4)    14       NNEENNWWSWSSSS   
(0, 0), (1, 1)    14       ENNEESWSSENSSS   
(0, 0), (1, 2)     7       ENNWSNN          
(0, 0), (1, 3)     9       NENNWSNNN        
(0, 0), (1, 4)    11       NNENNWSNNNN      
(0, 0), (2, 0)    14       NNEEESSWNSEENN   
(0, 0), (2, 1)     9       NEEESWEEN        
(0, 0), (2, 2)     9       EENNWSNNE        
(0, 0), (2, 3)    11       NEENNWSNNNE      
(0, 0), (2, 4)    13       NNEENNWSNNNNE    
(0, 0), (3, 0)    14       ENNEESSSWSWNSE   
(0, 0), (3, 1)    11       ENEEESWEEEN      
(0, 0), (3, 2)    11       NENEESWEENS      
(0, 0), (3, 3)    13       NNENEESWEENNS    
(0, 0), (3, 4)    15       NNNENEESWEENNNS  
(0, 0), (4, 0)    15       ENNEEESSWWSWWWN  
(0, 0), (4, 1)    13       EENEEESWEEEEN    
(0, 0), (4, 2)    13       NEENEESWEENSW    
(0, 0), (4, 3)    15       NNEENEESWEENNSW  
(0, 0), (4, 4)    17       NNNEENEESWEENNNSW

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 4/5/04.