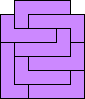
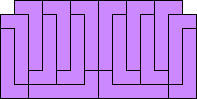
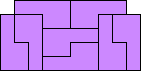
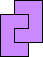Problem of the Month (March 2007)
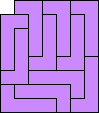
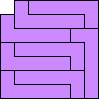
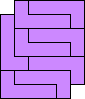
The problem of finding the order of a polyomino, the fewest number of copies of the polyomino that can tile a rectangle, has been well-studied. See Mike Reid's page for example. This month we study using polyominoes to tile rectangles with identical square corners missing. What are the smallest rectangles with 1×1 corners missing that polyominoes tile? What about rectangles with 2×2 or larger corners missing?
ANSWERS
Rectangles
1-5 1-5.gif)
|
|
6 6a.gif)
| 6b.gif)
(David Klarner)
| 6c.gif)
(T. W. Marlow)
|
|
7 7a.gif)
| 7b.gif)
(David Klarner)
| 7c.gif)
(T. W. Marlow)
|
|
8 8a.gif)
| 8d.gif)
(David Klarner)
| 8b.gif)
(Mike Reid)
| 8c.gif)
(Mike Reid)
|
|
10 10a.gif)
| 10b.gif)
| 10c.gif)
(William Marshall)
| 10d.gif)
(William Marshall)
|
|
11 11I.gif)
| 11L.gif)
| 11D.gif)
| 11B.gif)
| 11Q.gif)
| 11P.gif)
| 11O.gif)
(William Marshall)
| 11E.gif)
(Mike Reid)
|
|
Rectangles Without 1×1 Corners
1-4 1-4.gif)
|
|
5 5.gif)
|
|
6 6.gif)
|
|
7 7.gif)
|
7W.gif)
(Patrick Hamlyn)
| 7D.gif)
(Patrick Hamlyn)
| 7P.gif)
(Patrick Hamlyn)
| 7Q.gif)
(Mike Reid)
|
|
8 8a.gif)
| 8b.gif)
| 8c.gif)
| 8d.gif)
| 8J.gif)
(George Sicherman)
| 8P.gif)
(George Sicherman)
|
|
9 9.gif)
| 9P.gif)
(Patrick Hamlyn)
| 9D.gif)
(Patrick Hamlyn)
| 9J.gif)
(Patrick Hamlyn)
| 9A.gif)
(Mike Reid)
|
|
10 10a.gif)
| 10b.gif)
| 10c.gif)
| 10J.gif)
(Patrick Hamlyn)
| 10D.gif)
(Patrick Hamlyn)
| 10F.gif)
(Patrick Hamlyn)
|
|
11 11O.gif)
(George
Sicherman)
| 11P.gif)
(George
Sicherman)
| 11L.gif)
(George
Sicherman)
| 11Q.gif)
(George
Sicherman)
| 11I.gif)
(George Sicherman)
| 11J.gif)
(George Sicherman)
| 11D.gif)
(Mike Reid)
|
|
Rectangles Without 2×2 Corners
1-4 1-4.gif)
| 4T.gif)
(Patrick Hamlyn)
|
|
5 5.gif)
|
|
6 6.gif)
| 6B.gif)
(Patrick Hamlyn)
| 6Z.gif)
(Mike Reid)
| 6F.gif)
(Mike Reid)
| 6Y.gif)
(Mike Reid)
|
|
7 7.gif)
|
7B.gif)
(Patrick Hamlyn)
| 7P.gif)
(Patrick Hamlyn)
| 7D.gif)
(Mike Reid)
|
|
8 8a.gif)
| 8b.gif)
|
|
9 9.gif)
| 9Q.gif)
(Patrick Hamlyn)
| 9D.gif)
(Patrick Hamlyn)
|
9L.gif)
(Patrick Hamlyn)
| 9P.gif)
(Patrick Hamlyn)
| 9B.gif)
(Patrick Hamlyn)
| 9A.gif)
(Mike Reid)
| 9K.gif)
(Mike Reid)
|
|
10 10.gif)
| 10Q.gif)
(Mike Reid)
| 10A.gif)
(Mike Reid)
|
|
11 11P.gif)
(George
Sicherman)
| 11I.gif)
(George Sicherman)
| 11L.gif)
(George Sicherman)
| 11R.gif)
(George Sicherman)
| 11B.gif)
(George Sicherman)
| 11D.gif)
(George Sicherman)
| 11Q.gif)
(George Sicherman)
| 11O.gif)
(George Sicherman)
|
|
Rectangles Without 3×3 Corners
1-3 1-3.gif)
|
|
4 4.gif)
|
|
5 5.gif)
|
|
6 6a.gif)
| 6b.gif)
| 6L.gif)
(Patrick Hamlyn)
| 6K.gif)
(Mike Reid)
|
|
7 7.gif)
| 7P.gif)
(Patrick Hamlyn)
| 7L.gif)
(Patrick Hamlyn)
|
|
8 8.gif)
|
8P.gif)
(Patrick Hamlyn)
| 8L.gif)
(Patrick Hamlyn)
| 8Q.gif)
(Patrick Hamlyn)
|
|
10 10.gif)
| 10P.gif)
(Joe DeVincentis)
|
|
11 11P.gif)
(George Sicherman)
| 11D.gif)
(George Sicherman)
| 11I.gif)
(George Sicherman)
| 11O.gif)
(George Sicherman)
| 11L.gif)
(George Sicherman)
| 11Q.gif)
(George Sicherman)
| 11A.gif)
(Mike Reid)
|
|
Rectangles Without 4×4 Corners
1-3 1-3.gif)
|
|
4 4.gif)
|
|
5 5.gif) | 5Y.gif)
(Patrick Hamlyn)
|
|
7 7a.gif)
| 7b.gif)
|
|
8 8a.gif)
| 8b.gif)
| 8c.gif)
| 8E.gif)
(Patrick Hamlyn)
| 8K.gif)
(Mike Reid)
| 8Z.gif)
(Mike Reid)
|
|
9 9a.gif)
| 9b.gif)
| 9O.gif)
(Patrick Hamlyn)
| 9P.gif)
(Patrick Hamlyn)
| 9Q.gif)
(Patrick Hamlyn)
| 9L.gif)
(Patrick Hamlyn)
| 9D.gif)
(Patrick Hamlyn)
| 9C.gif)
(Mike Reid)
| 9S.gif)
(Mike Reid)
|
|
11 11I.gif)
(George Sicherman)
| 11L.gif)
(George Sicherman)
| 11B.gif)
(George Sicherman)
| 11D.gif)
(George Sicherman)
| 11Q.gif)
(George Sicherman)
| 11P.gif)
(George Sicherman)
| 11O.gif)
(George Sicherman)
|
|
Rectangles Without 5×5 Corners
1-3 1-3.gif)
|
|
4 4.gif)
| 4T.gif)
(Mike Reid)
|
|
5 5.gif) | 5Y.gif)
(Patrick Hamlyn)
|
|
6 6.gif)
| 6F.gif)
(Patrick Hamlyn)
| 6A.gif)
(Patrick Hamlyn)
| 6D.gif)
(Patrick Hamlyn)
| 6U.gif)
(Joe DeVincentis)
| 6G.gif)
(Mike Reid)
|
|
7 7.gif)
| 7P.gif)
(Patrick Hamlyn)
| 7D.gif)
(Patrick Hamlyn)
| 7L.gif)
(Patrick Hamlyn)
| 7Q.gif)
(Mike Reid)
| 7E.gif)
(Mike Reid)
|
|
8 8.gif)
| 8P.gif)
(Patrick Hamlyn)
| 8D.gif)
(Patrick Hamlyn)
| 8L.gif)
(Patrick Hamlyn)
| 8Q.gif)
(Patrick Hamlyn)
|
|
9 9.gif)
|
9B.gif)
(Patrick Hamlyn)
| 9O.gif)
(Patrick Hamlyn)
| 9Q.gif)
(Patrick Hamlyn)
|
9A.gif)
(Patrick Hamlyn)
| 9P.gif)
(Patrick Hamlyn)
| 9D.gif)
(Patrick Hamlyn)
|
9K.gif)
(Mike Reid)
|
|
10 10.gif)
|
|
Rectangles Without 6×6 Corners
3 3I.gif)
(Patrick Hamlyn)
| 3L.gif)
(Patrick Hamlyn)
|
|
4 4O.gif)
(Patrick Hamlyn)
| 4I.gif)
(Patrick Hamlyn)
| 4L.gif)
(Patrick Hamlyn)
| 4T.gif)
(Mike Reid)
|
|
5 5P.gif)
(Patrick Hamlyn)
| 5L.gif)
(Patrick Hamlyn)
| 5I.gif)
(Patrick Hamlyn)
| 5Y.gif)
(Patrick Hamlyn)
|
|
6 6O.gif)
(Patrick Hamlyn)
| 6I.gif)
(Patrick Hamlyn)
| 6L.gif)
(Patrick Hamlyn)
| 6P.gif)
(Patrick Hamlyn)
| 6U.gif)
(Patrick Hamlyn)
| 6A.gif)
(Patrick Hamlyn)
| 6F.gif)
(Patrick Hamlyn)
| 6D.gif)
(Patrick Hamlyn)
| 6R.gif)
(Patrick Hamlyn)
|
|
7 7P.gif)
(Patrick Hamlyn)
| 7L.gif)
(Patrick Hamlyn)
| 7I.gif)
(Patrick Hamlyn)
| 7D.gif)
(Patrick Hamlyn)
| 7Q.gif)
(Mike Reid)
|
|
8 8O.gif)
(Patrick Hamlyn)
| 8P.gif)
(Patrick Hamlyn)
| 8D.gif)
(Patrick Hamlyn)
| 8Q.gif)
(Patrick Hamlyn)
| 8L.gif)
(Patrick Hamlyn)
| 8I.gif)
(Patrick Hamlyn)
| 8K.gif)
(Mike Reid)
|
|
10 10Y.gif)
(Mike Reid)
|
|
11 11O.gif)
(Mike Reid)
|
|
Patrick Hamlyn also considered the variant where non-symmetric polyominoes could not be flipped over. Even-sized corners were not very exciting, but here are the best results for odd-sized corners:
Rectangles Without 1×1 Corners
x4L.gif)
(Patrick Hamlyn)
| x5P.gif)
(Patrick Hamlyn)
| x5L.gif)
(Patrick Hamlyn)
| x5Y.gif)
(Patrick Hamlyn)
| x6W.gif)
(Patrick Hamlyn)
| x6P.gif)
(Patrick Hamlyn)
|
x7P.gif)
(Patrick Hamlyn)
| x8P.gif)
(Patrick Hamlyn)
|
x9P.gif)
(Patrick Hamlyn)
| x9Q.gif)
(Patrick Hamlyn)
| x9D.gif)
(Patrick Hamlyn)
| x11P.gif)
(Patrick Hamlyn)
|
Rectangles Without 3×3 Corners
x4L.gif)
(Patrick Hamlyn)
| x5P.gif)
(Patrick Hamlyn)
| x5L.gif)
(Patrick Hamlyn)
| x7P.gif)
(Patrick Hamlyn)
|
x8P.gif)
(Patrick Hamlyn)
| x9P.gif)
(Patrick Hamlyn)
| x11P.gif)
(Patrick Hamlyn)
|
Rectangles Without 5×5 Corners
x4L.gif)
(Patrick Hamlyn)
| x5P.gif)
(Patrick Hamlyn)
| x5Y.gif)
(Patrick Hamlyn)
|
x6P.gif)
(Patrick Hamlyn)
| x7P.gif)
(Patrick Hamlyn)
| x8P.gif)
(Patrick Hamlyn)
|
x9D.gif)
(Patrick Hamlyn)
| x9O.gif)
(Patrick Hamlyn)
| x9P.gif)
(Patrick Hamlyn)
|
x10F.gif)
(Patrick Hamlyn)
| x10P.gif)
(Patrick Hamlyn)
| x10O.gif)
(Patrick Hamlyn)
|
Ed Pegg thought these tilings were worthy of mention, even if they don't exactly meet this month's criteria:
George Sicherman found tilings of rectangles missing only one 1×1 corner...
...two opposite 1×1 corners...
...two adjacent 1×1 corners...
...and three 1×1 corners.
Brian Astle thought that the smallest square missing two opposite 1×1 corners that could be tiled by more than 2 polyominoes other than monominoes was an 18×18 square tiled with 46 copies of a heptomino. Mike Reid found that a 10×10 square could be tiled with 14 copies of a different heptomino.
Brian Astle also conjectured that no square missing opposite corners could be tiled with an odd number of polyominoes, but Mike Reid found a counterexample using 41 heptominoes to tile a 17×17 square.
Claudio Baiocchi noted that if two copies of a polyomino could tile a 4×5 rectangle, then there are trivial tilings of rectangles missing 4×4 or 5×5 corners:
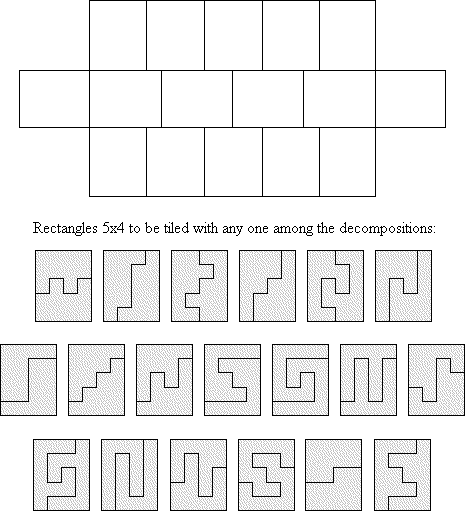
Gavin Theobold noted the same trick works for other size rectangles too.
If you can extend any of these results, please
e-mail me.
Click here to go back to Math Magic. Last updated 3/31/07.
9a.gif)
9b.gif)
9c.gif)
9d.gif)
9a.gif)
9b.gif)
9c.gif)
9e.gif)
9d.gif)
9P.gif)
6a.gif)
6b.gif)
6K.gif)
10a.gif)
10b.gif)
10c.gif)
10d.gif)
10K.gif)