




 |  |  |  |  |
What are the answers for large m and n?
It is easy to show:
f(1,n) = 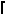 n/2
n/2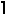
f(2,n) = 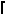 n/3
n/3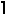
f(3,n) = 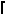 n/4
n/4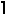 for n≥2
for n≥2
f(4,n) = 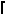 n/5
n/5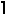 for n≥3
for n≥3
f(5,n) = 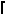 n/5
n/5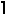 for n≥12
for n≥12
f(6,1) = 3
f(6,6n) = n
f(6,6n+i) = n+2 for 1≤i≤4
f(6,6n+5) = n+3
Joe DeVincentis showed that f(7,6n+i) = 2n+2 for 1≤i≤2 and f(7,6n+i) = 2n+3 for 3≤i≤6.
Joe DeVincentis conjectured that f(8,3n–i) = n+2 for 0≤i≤2 and n≥10. He showed this pattern is eventually optimal, with limiting efficiency 24.
Joe DeVincentis also showed that the width 9 rectangles eventually have period 10 with limiting efficiency 30.
What is the eventual behavior of f(m,n) for larger m?
| m\n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 6 | 6 | 7 | 7 | 8 | 8 | 9 | 9 | 10 | 10 | 11 | 11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 9 | 10 | 10 | 10 | 11 | 11 | 11 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 2 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 6 | 6 | 6 | 6 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 2 | 2 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 6 | 6 | 6 | 6 | 6 | 7 | 7 | 7 | 7 | 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 3 | 2 | 2 | 1 | 1 | 3 | 3 | 2 | 2 | 2 | 4 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 6 | 6 | 6 | 6 | 6 | 7 | 7 | 7 | 7 | 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 3 | 2 | 2 | 2 | 3 | 1 | 3 | 3 | 3 | 3 | 4 | 2 | 4 | 4 | 4 | 4 | 5 | 3 | 5 | 5 | 5 | 5 | 6 | 4 | 6 | 6 | 6 | 6 | 7 | 5 | 7 | 7 | 7 | 7 | 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 4 | 3 | 2 | 2 | 3 | 3 | 4 | 4 | 4 | 5 | GS | JD | JP | JG | 7 | 7 | JD | JD | JD | JD | 9 | 9 | JD | JD | JD | JD | 11 | 11 | JD | JD | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 4 | 3 | 2 | 2 | 2 | 3 | 4 | 4 | 4 | 4 | 5 | JD | 6 | 6 | 6 | 7 | 8 | 8 | 8 | 8 | 9 | 10 | 10 | 10 | 10 | 11 | JD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 5 | 3 | 3 | 2 | 2 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 6 | 6 | 6 | 7 | JP | 8 | 8 | 8 | 9 | 9 | JD | 10 | 10 | JD | 11 | JD | JD | JD | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 5 | 4 | 3 | 2 | 2 | 3 | 5 | 4 | 4 | 4 | JP | 5 | 6 | 6 | 6 | JP | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | JD | 10 | 10 | 11 | 11 | 11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | 6 | 4 | 3 | 3 | 4 | 4 | GS | 5 | 5 | JP | JD | 5 | JD | JD | JD | JD | JD | 7 | JD | 8 | 8 | 8 | 9 | JP | JD | JP | JP | JD | 11 | JD
| 12
| 6 | 4 | 3 | 3 | 3
| 2
| JD
| JD
| 5
| 5
| 5
| 4
| 7
| JD
| 7
| 7
| 7
| 6
| JD
| 9
| 9 | 9 | 9 | 8 | 9
| 11 | 11 | 11 | 11 | 10
| 11
| 13
| 7 | 5 | 4 | 3 | 3
| 4 | JP | 6 | 6 | 6
| JD | 7 | JG | JD | JD
| JD | JD | JD | JD | JD
| JD
| JD
| JD
| JD
| 14
| 7 | 5 | 4 | 3 | 3
| 4 | JG | 6 | 6 | 6
| JD | JD | JD | JD | JD
| JD | JD | JG | JD
| JD
| 11
| JD
| JD
| JD
| 15
| 8 | 5 | 4 | 3 | 3
| 4 | 7 | 6 | 6 | 6
| JD
| 7 | JD | JD | 9
| EF | 10 | JG | JD | JD
| JD
|
| JD
| JD
| JD
| 16
| 8 | 6 | 4 | 4 | 4
| 4 | 7 | 7 | 7 | JP
| JD | 7 | JD | JD | EF
| JG | JD | JP
| JD
| JD
| 17
| 9 | 6 | 5 | 4 | 4
| 5 | JD
| 8 | JP | 7
| JD | 7 | JD | JD | 10
| JD | JG | JP | JD
| 18
| 9 | 6 | 5 | 4 | 4
| 3 | JD | 8 | 8 | 7
| 7 | 6 | JD | JG | JG
| JP | JP | 9 | JD
| 19
| 10 | 7 | 5 | 4 | 4
| 5 | JD | 8 | 8 | 8
| JD | JD | JD
| JD | JD
| JD | JD | JD
| 20
| 10 | 7 | 5 | 4 | 4
| 5 | JD | 8 | 8 | 8
| 8 | 9 | JD
| JD
| JD
| JD
| 21
| 11 | 7 | 6 | 5 | 5
| 5 | 9 | 9 | 9 | 8
| 8 | 9 | JD
| 11
| JD
| 22
| 11 | 8 | 6 | 5 | 5
| 5 | 9 | 10 | 9 | 8
| 8 | 9 | JD | JD
| 23
| 8 | 6 | 5 | 5
| 6 | JD
| 10 | JD
| 9
| 9 | 9 | JD
| JD | JD
| 24
| 8 | 6 | 5 | 5
| 4 | JD | 10 | 10 | 9
| JP | 8 | JD | JD | JD
| 25
| 9 | 7 | 5 | 5
| 6 | JD | 10 | 10 | JD
| JD | 9 | JD
| 26
| 9 | 7 | 6 | 6
| 6 | JD | 11 | JD
| 10
| JP | 11
| 27
| 9 | 7 | 6 | 6
| 6 | 11 | JD | 11 | 10
| JP | 11
| 28
| 10 | 7 | 6 | 6
| 6 | 11
| JD
| 11 | JD
| 11
| 29
| 10 | 8 | 6 | 6 | 7
| JD | JD
| 11 | 11 | 11
| 30
| 10 | 8 | 6 | 6
| 5 | JD | JD
| 11
| JD
| 10
| 31
| 11 | 8 | 7 | 7
| 7 | 11
| 32
| 11 | 8 | 7 | 7
| 7
| 33
| 11 | 9 | 7 | 7
| 7
| 34
| 9 | 7 | 7
| 7
| 35
| 9 | 7 | 7 | 8
| |
Jeremy Galvagni tried to cover a 100×100 square to see whether small, medium, or large circles were most efficient. By using a large circle, he managed a covering with 145 circles. Joe DeVincentis improved this to 129 circles, shown below. Can anyone do better?

Jeremy Galvagni also defined the covering efficiency of a covering as the area covered per circle. He notes that the multiples of the 6×6 packing of one circle all have efficiency 36. He asked for the smallest covering that is more efficient than this. Joe DeVincentis found a covering of a 22×22 square with a higher efficiency, shown below.

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 3/31/13.