Problem of the Month
(March 2014)
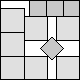
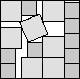
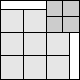
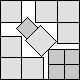
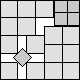
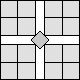
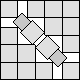
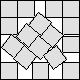
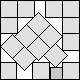
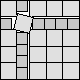
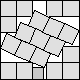
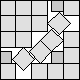
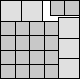
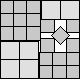
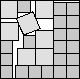
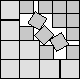
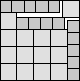
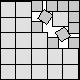
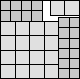
What is the smallest square that n squares of area 1 and m squares of area 2 can be packed into? Can you improve or extend these packings?
ANSWERS
Solutions were received from Maurizio Morandi, Jeremy Galvagni, and Joe DeVincentis.
| m \ n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10
|
|---|
| 0
| 0
| 1

| 2
| 2
| 2

| 2+√2/2
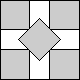
| 3
| 3
| 3
| 3

| 3+√2/2
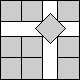
|
|---|
| 1
| √2

| 1+√2
| 1+√2
| 1+√2

| 3
| 3

| (5+√3)/2(MM)
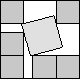
| 2+√2
| 2+√2
| (5+√7)/2(MM)
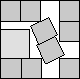
| 3.978 (MM)

|
|---|
| 2
| 2√2
| 2√2
| 2√2
| 3

| 2+√2
| 2+√2
| 2+√2
| 2+√2

| 3.883 (MM)
| 4
| 4

|
|---|
| 3
| 2√2
| 2√2
| 2+√2
| 2+√2
| 2+√2

| 8√2/3 (MM)
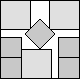
| 1+2√2
| 3.883 (MM)

| 4
| 4.297 (MM)

| 3+√2
|
|---|
| 4
| 2√2

| 5√2/2
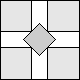
| 1+2√2
| 1+2√2
| 1+2√2
| 1+2√2

| 4
| 4

| 4.346 (MM)

| 3+√2
| 3+√2
|
|---|
| 5
| 1+2√2
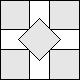
| 2+4√2/3(MM)
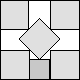
| 3.887
| 3.887
| 3.887

| 3√2
| 3+√2
| 3+√2
| 3+√2
| 3+√2

| 2+2√2
|
|---|
| 6
| 3√2
| 3√2
| 3√2
| 3√2
| 3√2

| 3+√2

| 4.676 (MM)

| 2+2√2
| 2+2√2
| 2+2√2
| 2+2√2

|
|---|
| 7
| 3√2
| 3√2
| 3√2
| 3+√2

| 1/2+3√2(MM)
| 2+2√2
| 2+2√2
| 2+2√2
| 2+2√2

| 5.203 (MM)
| 1+3√2
|
|---|
| 8
| 3√2
| 3√2
| 2+2√2
| 2+2√2
| 2+2√2
| 3+3/√2(MM)
| 5.215
| 5.215
| 5.215 (JD)

| 1+3√2
| 1+3√2
|
|---|
| 9
| 3√2

| 7√2/2
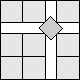
| 5.119 (MM)
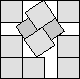
| 1+3√2
| 1+3√2
| 1+3√2
| 1+3√2
| 1+3√2
| 1+3√2
| 1+3√2

| 4√2

|
|---|
| 10
| 1+3√2
| 1+3√2
| 1+3√2
| 1+3√2
| 1+3√2
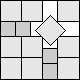
| 2+7√2/3(MM)
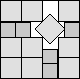
| 5.302 (MM)

| 5.576 (MM)
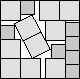
| 5.613 (JD)

| 5.711 (MM)

| 3+2√2
|
|---|
| 11
| 5.482
| 5.482 (MM)

| 5.523 (MM)
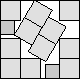
| 2+5/√2(MM)

| 4/3+3√2(JD)
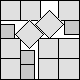
| 5.607 (JD)

| 4√2
| 4√2(MM)

| 5.760 (MM)

| 3+2√2
| 3+2√2
|
|---|
| 12
| 4√2
| 4√2
| 4√2
| 4√2
| 4√2
| 4√2
| 3+2√2
| 3+2√2
| 3+2√2
| 3+2√2

| 2+3√2
|
|---|
| 13
| 4√2
| 4√2
| 4√2
| 4√2
| 4√2

| 3+2√2

| 6.090 (MM)

| 2+3√2
| 2+3√2
| 2+3√2
| 2+3√2

|
|---|
| 14
| 4√2
| 4√2
| 4√2
| 3+2√2

| 1/2+4√2(MM)
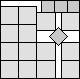
| 2+3√2
| 2+3√2
| 2+3√2
| 2+3√2

| 6.521 (MM)

| 6.630
|
|---|
| 15
| 4√2
| 4√2
| 2+3√2
| 2+3√2
| 2+3√2

| 9/√2
| 6.521 (MM)

| 6.630
| 6.630 (MM)

| 1+4√2
| 1+4√2
|
|---|
| 16
| 4√2

| 9/√2
| (3+7√2)/2(MM)
| 6.607 (MM)

| (10+7√2)/3(MM)

| 1+4√2
| 1+4√2
| 1+4√2
| 1+4√2
| 1+4√2
| 1+4√2

|
|---|
| 17
| 6.611
| (10+7√2)/3(MM)
| 1+4√2
| 1+4√2
| 1+4√2
| 1+4√2
| 1+4√2
| 1+4√2
| 1+4√2

| 6.827
| 6.827 (JD)
|
|---|
| 18
| (7+√7)/√2
| (7+√7)/√2
| (7+√7)/√2
| (7+√7)/√2
| (7+√7)/√2
| (7+√7)/√2

| 6.821 (JD)

| 6.886 (JD)

| 5√2
| 5√2
| 5√2

|
|---|
| 19
| 3√2+8/3

| 6.921 (JD)
| 6.922 (JD)

| 4/3+4√2(JD)
| 7.020 (JD)

| 7.021 (JD)
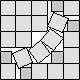
| 5√2
| 5√2
| 5√2
| 7.125 (MM)

| 3+3√2
|
|---|
| 20
| 5√2
| 5√2
| 5√2
| 5√2
| 5√2
| 5√2
| 5√2
| 5√2

| 7.174 (MM)

| 3+3√2
| 3+3√2

|
|---|
| m \ n | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20
|
|---|
| 0
| 3.877

| 4
| 4
| 4
| 4
| 4

| 4.675
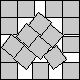
| (7+√7)/2
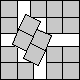
| 3+4√2/3

| 5
|
|---|
| 1
| 4
| 4

| 4.362 (MM)
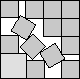
| 3+√2
| 3+√2
| 4+1/√2(MM)
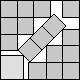
| 4.839 (MM)

| 5
| 5
| 5
|
|---|
| 2
| 4.365 (MM)
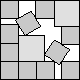
| 3+√2
| 3+√2
| 3+√2
| (7+√7)/2(MM)
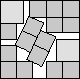
| 4+2/√5(MM)

| 5
| 5
| 5

| 5.350 (MM)

|
|---|
| 3
| 3+√2
| 3+√2
| 3+√2(MM)

| 2+2√2(MM)
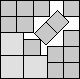
| 5
| 5
| 5
| 5.297 (MM)
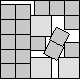
| 4+√2
| 4+√2
|
|---|
| 4
| 4.764 (MM)
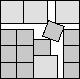
| 2+2√2
| 4.893 (MM)

| 5
| 5
| 5

| 5.346 (MM)

| 4+√2
| 4+√2
| 4+√2(MM)

|
|---|
| 5
| 2+2√2
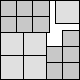
| 5
| 5 (MM)
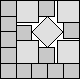
| 1+3√2
| 5.378 (MM)

| 4+√2
| 4+√2
| 4+√2(MM)
| 5.764 (MM)

| 3+2√2
|
|---|
| 6
| 5 (MM)

| 1+3√2
| 1+3√2

| 4+√2
| 4+√2
| 4+√2(MM)

| 4√2
| 3+2√2
| 3+2√2
| 9/2+√2(MM)
|
|---|
| 7
| 1+3√2

| 4+√2
| 4+√2
| 4√2
| 4√2
| 4√2

| 3+2√2
| 3+2√2
| 6
| 6.203 (MM)
|
|---|
| 8
| 4+√2
| 4+√2(MM)

| 5.776 (MM)
| 3+2√2
| 3+2√2
| 3+2√2
| 3+2√2(MM)

| 6

| 6.215 (MM)

| 2+3√2
|
|---|
| 9
| 5.779 (MM)

| 3+2√2
| 3+2√2
| 3+2√2
| 6.085 (JD)

| 2+3√2
| 2+3√2
| 2+3√2
| 2+3√2
| 2+3√2

|
|---|
| 10
| 3+2√2
| 3+2√2
| 3+2√2(MM)

| 2+3√2
| 2+3√2
| 2+3√2
| 6.302 (MM)

| 5+√2
| 5+√2(MM)

| 1+4√2
|
|---|
| 11
| 6.179 (MM)

| 2+3√2
| 2+3√2
| 2+3√2
| 2+3√2
| 5+√2

| 6.593 (MM)

| 1+4√2
| 1+4√2(MM)

| 4+2√2
|
|---|
| 12
| 2+3√2
| 2+3√2
| 2+3√2
| 2+3√2(MM)

| 6.525 (JD)

| 1+4√2
| 1+4√2
| 6.764 (JD)

| 4+2√2
| 4+2√2

|
|---|
| 13
| 2+3√2
| 2+3√2(MM)

| 6.630 (JD)

| 1+4√2
| 1+4√2
| 1+4√2(MM)

| 4+2√2
| 4+2√2

| 5√2
| 5√2
|
|---|
| 14
| 6.630 (JD)

| 1+4√2
| 1+4√2
| 1+4√2(MM)
| 4+2√2
| 4+2√2(MM)

| 5√2
| 5√2
| 5√2

| 3+3√2
|
|---|
| 15
| 1+4√2
| 1+4√2
| 4+2√2
| 4+2√2
| 5√2
| 5√2
| 5√2
| 3+3√2
| 3+3√2
| 3+3√2
|
|---|
| 16
| 1+4√2

| 4+2√2
| 4+2√2(MM)

| 5√2
| 5√2
| 5√2(MM)

| 3+3√2
| 3+3√2
| 3+3√2
| 7.593 (MM)

|
|---|
| 17
| 5√2
| 5√2

| 7.190 (MM)

| 3+3√2
| 3+3√2
| 3+3√2
| 3+3√2
| 3+3√2(MM)

| 7.630 (JD)

| 2+4√2
|
|---|
| 18
| 7.193 (MM)
| 3+3√2
| 3+3√2
| 3+3√2
| 7.499 (JD)

| 2+4√2
| 2+4√2
| 2+4√2
| 2+4√2
| 2+4√2(MM)
|
|---|
| 19
| 3+3√2
| 3+3√2
| 3+3√2(MM)

| 2+4√2
| 2+4√2
| 2+4√2
| 2+4√2
| 2+4√2
| 5+2√2
| 5+2√2(MM)

|
|---|
| 20
| 7.593 (JD)

| 2+4√2
| 2+4√2
| 2+4√2
| 2+4√2
| 2+4√2
| 2+4√2(MM)

| 5+2√2(MM)

| 8.045 (JD)

| 1+5√2

|
|---|
Jeremy Galvagni noticed that multiplying the (m,n) packing by √2 gives a (n,4m) packing.
If you can extend any of these results, please
e-mail me.
Click here to go back to Math Magic. Last updated 3/29/15.











































































































































































