Problem of the Month (April 2005)
Start with a horizontal line called the ground. We say a tent is a collection of unit line segments that are only joined to the top half of the ground and each other at their endpoints. We call a tent rigid if its framework of segments is rigid in the plane as long as the connections to the ground are fixed. We define the area of a tent to be the area enclosed by the tent and ground.
It is well-known that the tent made of n segments with the largest area is half a 2n-gon. This month's problem is to investigate the rigid tent made from n segments with the largest area. What are the best results for various n? Can you give lower or upper bounds for the largest possible area? Since I turn 40 this month, I'll give a special prize of $10 to the person who can enclose the largest area with 40 rigid unit segments.
ANSWERS
Clinton Weaver improved my area for n=5 to A = √3 = 1.732+.
George Sicherman asks what the largest rigid tent is using n segments with no triangles. Can this be done at all?
Guenter Stertenbrink wonders what the largest rigid structures are with no line to connect to. I think the answers are usually collections of equilateral triangles, though for n=15 this is not the case!
Guenter Stertenbrink also gives an application of this month's problem. A bacteria farmer wants to enclose the largest combined area against shore using n equal length planks that can only be fastened at the ends.
Claudio Baiocchi notes that for large n, trapezoid structures can have area at most 2n3/2/3√3, but rectangle structures can have areas at least n2/(6+√6).
Here are the maximum areas so far:
Largest Areas of Rigid Tents Using n Unit Segments
| n | Largest Area | Author | Picture |
|---|
| 2 | 0.500 | EF | 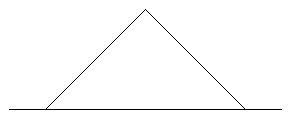 |
| 4 | 1.299 | EF |  |
| 5 | 1.732 | CW, DL | 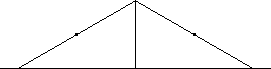 |
| 6 | 2.414 | EF, CP, DL | 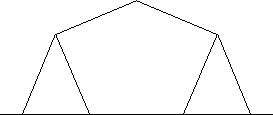 |
| 7 | 3.148 | EF, JD, CP, DL, GS |  |
| 8 | 4.116 |
| 9 | 5.095 |
| 10 | 6.080 |
| 11 | 7.069 |
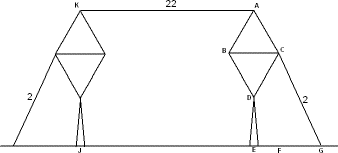
| 12 | 8.096 | CP | 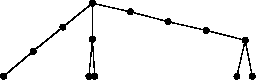 |
| 13 | 9.628 |
| 14 | 11.148 |
| 15 | 12.661 |
| 16 | 14.171 |
| 17 | 15.679 |
| 18 | 17.184 |
| 19 | 18.689 |
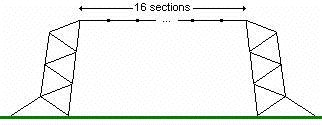
| 20 | 20.472 | EF, CP, BF |  |
| 21 | 22.472 |
| 22 | 24.472 |
| 23 | 26.472 |
| 24 | 28.472 |
| 25 | 30.472 |
| 26 | 32.472 |
| 27 | 34.472 |
| 28 | 36.518 | BJ |  |
| 29 | 39.016 |
| 30 | 41.513 |
| 31 | 44.011 |
| 32 | 46.509 |
| 33 | 49.007 |
| 34 | 51.505 |
| 35 | 54.004 |
| 36 | 56.502 |
| 37 | 59.084 | GS |  |
| 38 | 61.937 | BF, CP |  |
| 39 | 64.937 |
| 40 | 67.937 |
| 41 | 70.937 |
| 42 | 73.937 |
| 43 | 76.937 |
| 44 | 79.937 |
| 45 | 82.937 |
| 46 | 85.937 |
| 47 | 88.937 |
| 48 | 91.937 |
| 49 | 94.937 |
| 50 | 97.937 |
Here are the best areas that people managed to contain with 40 rigid segments:
Largest Areas of Rigid Tent With n=40
| Name | Best Area
|
|---|
| Bertram Felgenhauer | 67.93
|
| Brian J | 67.93
|
| Dan Dima | 67.93
|
| Dave Langers | 67.93
|
| Corey Plover | 67.93
|
| Guenter Stertenbrink | 67.54
|
| Emilio Schiavi | 63.91
|
| Erich Friedman | 63.80
|
| Andrew Bayly | 63.80
|
| David Cantrell | 63.74
|
| Gary Gerken | 58.80
|
| George Sicherman | 56.14
|
| Joseph DeVincentis | 53.68
|
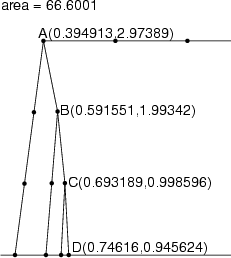
The best rigid tent for n=40 is the last picture shown above. Bertram Felgenhauer wins the $10 prize. Here are some of the other solutions I received:

If you can extend any of these results, please
e-mail me.
Click here to go back to Math Magic. Last updated 4/29/05.