| Copies | Smallest | Area |
|---|---|---|
| 4 |  | 1 |
| 3 | 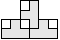 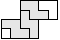 | 4 |
| 2 | 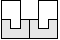 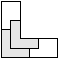 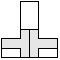 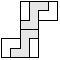 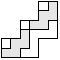 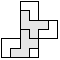 | 5 |
| 1 |  | 5 |
| 0 |  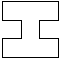 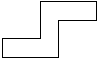 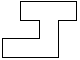 | 7 |
| Copies | Smallest | Area |
|---|---|---|
| 4 |  | 1 |
| 3 |   | 4 |
| 2 |       | 5 |
| 1 |  | 5 |
| 0 |     | 7 |
| Copies | Smallest | Area |
|---|---|---|
| 4 |  | 1 |
| 3 | 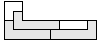 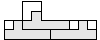 | 6 |
| 2 |   | 5 |
| 1 | 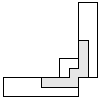 (and 19 others) (and 19 others) | 9 |
| 0 |     | 7 |
| Copies | Smallest | Area |
|---|---|---|
| 4 |  | 1 |
| 3 | 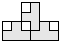 | 4 |
| 2 | 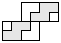 | 4 |
| 1 |  | 5 |
| 0 |     | 7 |
| Copies | Smallest | Area |
|---|---|---|
| 4 |  | 1 |
| 3 | 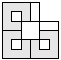 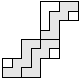 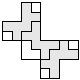 | 7 |
| 2 | 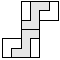   | 5 |
| 1 | 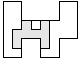 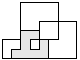 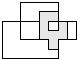 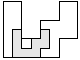 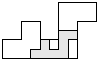 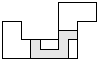 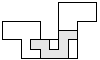 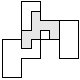 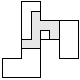 | 8 |
| 0 |     | 7 |
| Copies | Smallest | Area |
|---|---|---|
| 4 |  | 1 |
| 3 | 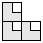 | 3 |
| 2 | 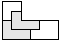 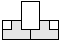 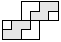 | 4 |
| 1 | 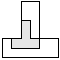 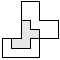  | 5 |
| 0 |     | 7 |
| Copies | Smallest | Area |
|---|---|---|
| 4 |  | 1 |
| 3 |  | 3 |
| 2 | 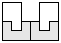 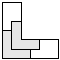 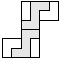 | 5 |
| 1 | 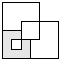 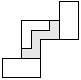 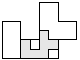 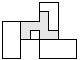 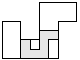 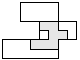 | 7 |
| 0 |     | 7 |
| Copies | Smallest | Area |
|---|---|---|
| 9 |  | 1 |
| 8 | 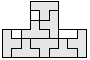 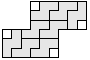 | 4 |
| 7 | 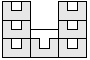 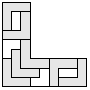 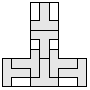 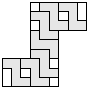 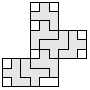 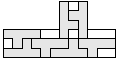 | 5 |
| 6 |  | 5 |
| 5 | 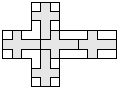  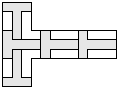 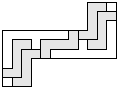 | 6 |
| 4 | 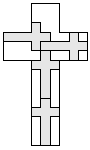 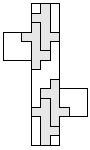 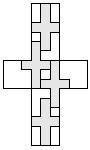 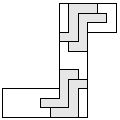 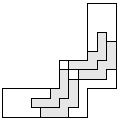 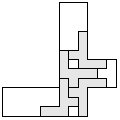 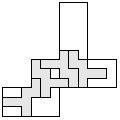  | 7 |
| 3 | 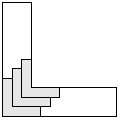 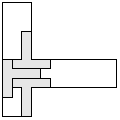 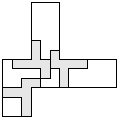 | 7 |
| 2 | 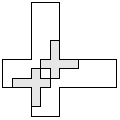 | 7 |
| 1 |  | 9 |
| 0 |   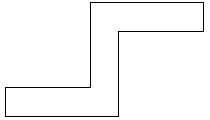 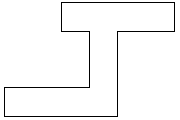 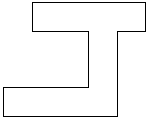  | 10 |
| Copies | Smallest | Area |
|---|---|---|
| 9 |  | 1 |
| 8 |  | 4 |
| 7 | 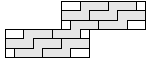 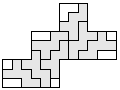 | 6 |
| 6 | 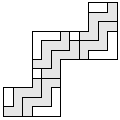 | 7 |
| 5 | 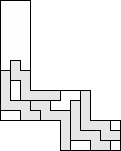 (George Sicherman) | 8 |
| 4 | 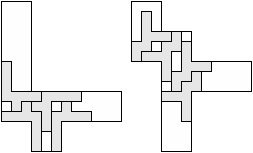 (George Sicherman) | 8 |
| 3 |  | 7 |
| 2 | 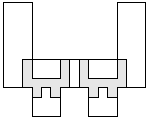 (and 17 others) (and 17 others) | 11 |
| 1 | 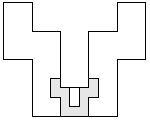 | 11 |
| 0 |       | 10 |
| Copies | Smallest | Area |
|---|---|---|
| 9 |  | 1 |
| 8 | 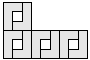  | 4 |
| 7 | 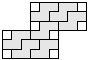 | 4 |
| 6 | 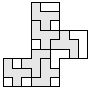  | 5 |
| 5 |    | 6 |
| 4 | 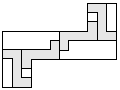 | 6 |
| 3 | 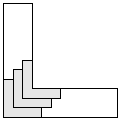 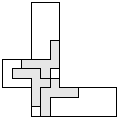 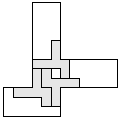 | 7 |
| 2 | 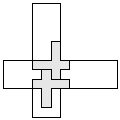 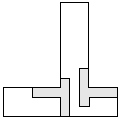 | 7 |
| 1 | 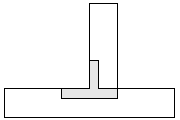  | 9 |
| 0 |       | 10 |
| Copies | Smallest | Area |
|---|---|---|
| 9 |  | 1 |
| 8 |   | 5 |
| 7 |  | 4 |
| 6 | 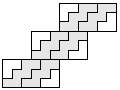 | 6 |
| 5 | 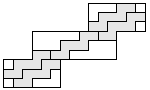 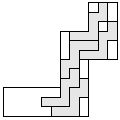 | 7 |
| 4 | 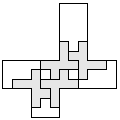 | 7 |
| 3 | 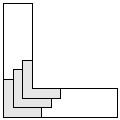 | 7 |
| 2 | 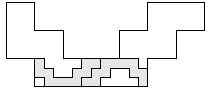 (and 44 others) (and 44 others) | 11 |
| 1 | 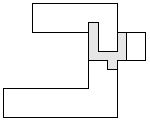 | 10 |
| 0 |       | 10 |
| Copies | Smallest | Area |
|---|---|---|
| 9 |  | 1 |
| 8 | 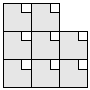 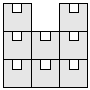 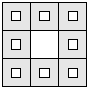 | 8 |
| 7 | 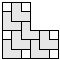 | 3 |
| 6 | 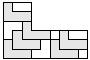 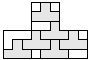 | 4 |
| 5 | 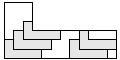 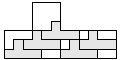 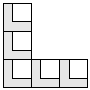 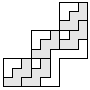 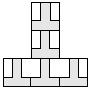 | 5 |
| 4 | 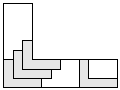 (and 10 others) (and 10 others) | 5 |
| 3 | 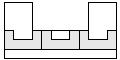 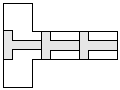 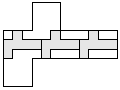 | 5 |
| 2 | 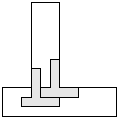 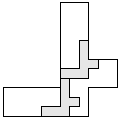 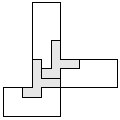 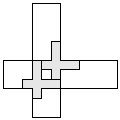 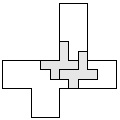 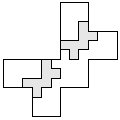 | 7 |
| 1 | 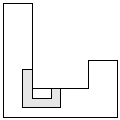 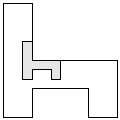 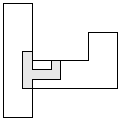 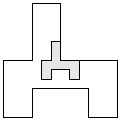 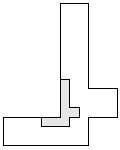 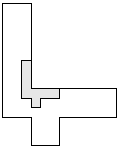 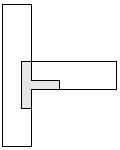 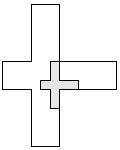 | 8 |
| 0 |       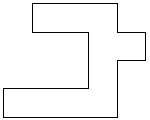 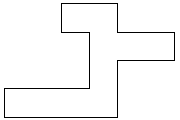 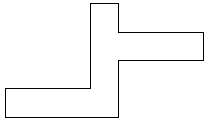 | 10 |
| Copies | Smallest | Area |
|---|---|---|
| 9 |  | 1 |
| 8 |    | 8 |
| 7 |  | 3 |
| 6 | 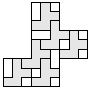 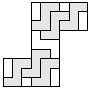 | 5 |
| 5 | 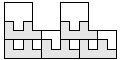 | 6 |
| 4 | 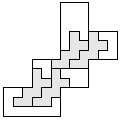 | 7 |
| 3 | 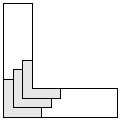 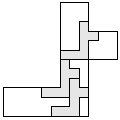 | 7 |
| 2 | 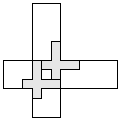 | 7 |
| 1 | 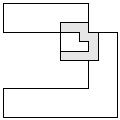 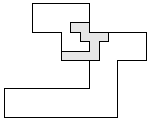 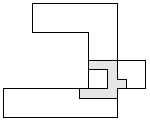 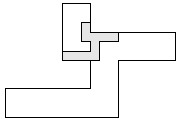 | 10 |
| 0 |        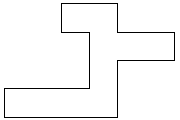 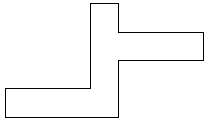 | 10 |
| Copies | Smallest | Area | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16 |  | 1 | |||||||||||||||||||||||||||||||||||||||||||||
| 15 | ? | ?
| 14 | 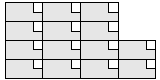 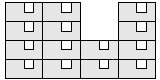 7
| 13 | 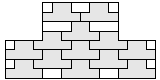 6
| 12 | 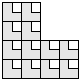 3
| 11 | 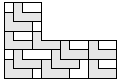 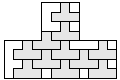 4
| 10 | 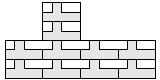 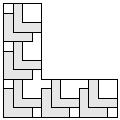  5
| 9 | 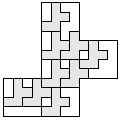 5
| 8 | 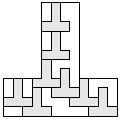 5
| 7 | 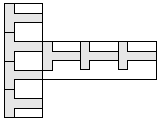 6
| 6 | 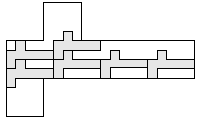 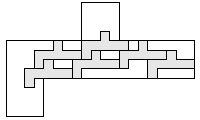 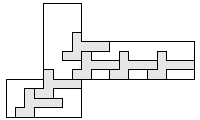 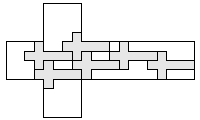 7
| 5 | 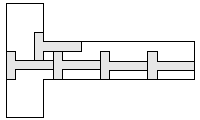 7
| 4 | 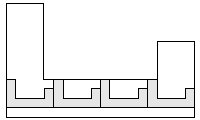 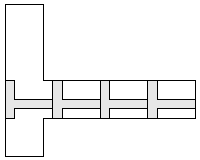 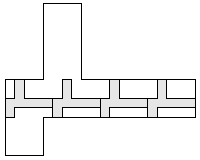 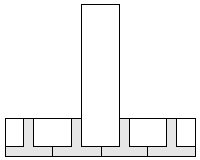 8
| 3 | 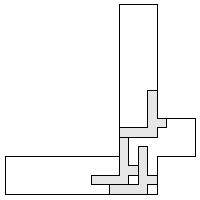 (and 10 others) (and 10 others) 9
| 2 | 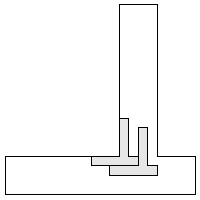 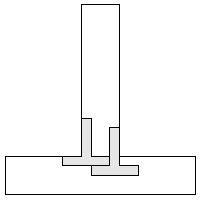 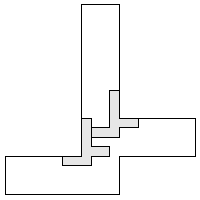 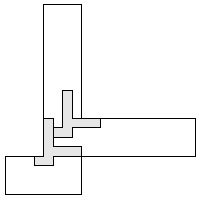 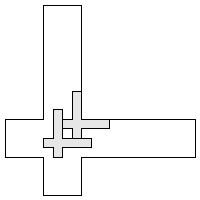  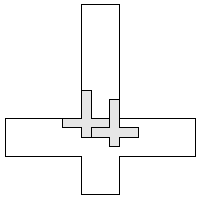 9
| 1 | 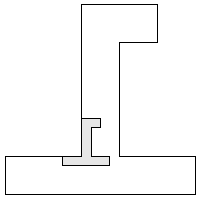 10
| 0 |  (and 17 others) (and 17 others)(George Sicherman) 13
| |
| Copies | Smallest | Area | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16 |  | 1 | |||||||||||||||||||||||||||||||||||||||||||||
| 15 | ? | ?
| 14 |   7
| 13 |  6
| 12 | 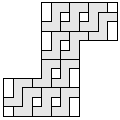 5
| 11 | 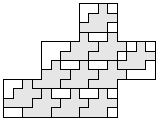 7
| 10 | 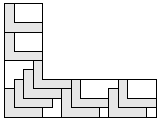 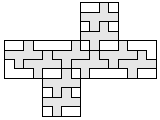 6
| 9 | 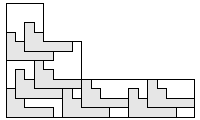  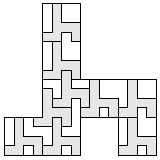 8
| 8 | 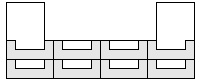 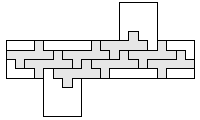 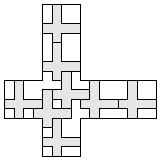 7
| 7 | 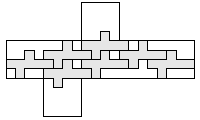 7
| 6 | 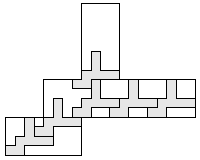 8
| 5 | 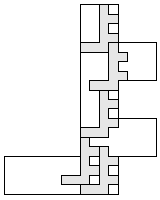 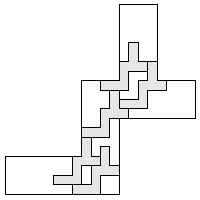 9
| 4 | 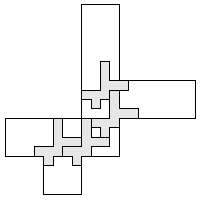 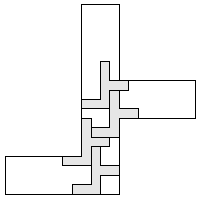 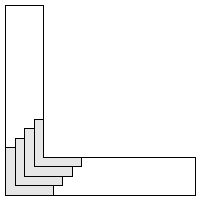 9
| 3 |  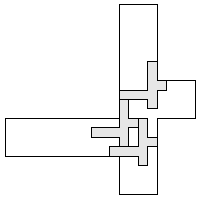 9
| 2 | 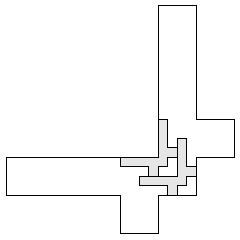 (and 21 others) (and 21 others) 11
| 1 | 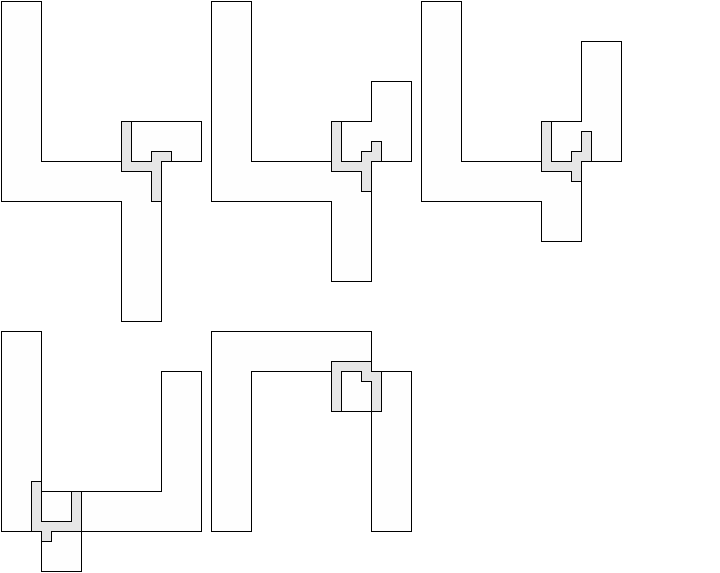 (George Sicherman) 13
| 0 |  (and 17 others) (and 17 others)(George Sicherman) 13
| |
| Copies | Smallest | Area |
|---|---|---|
| 16 |  | 1 |
| 15 | 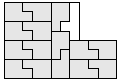 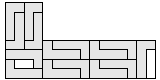 | 5 |
| 14 | 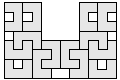 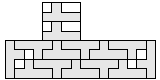 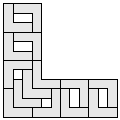 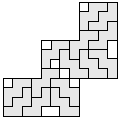 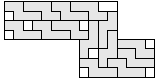 | 5 |
| 13 | 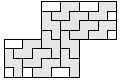 | 4 |
| 12 | 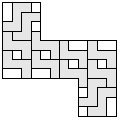 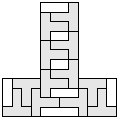 | 5 |
| 11 | 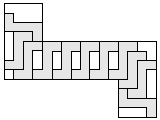 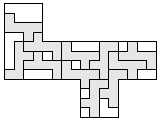   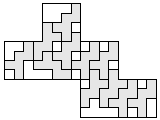  | 6 |
| 10 |  | 5 |
| 9 | 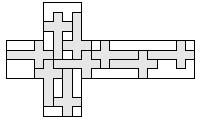 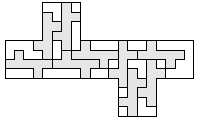 | 7 |
| 8 | 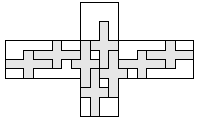 | 7 |
| 7 | 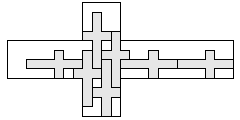 | 8 |
| 6 | 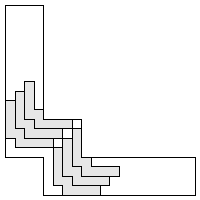 (and 9 others) (and 9 others) | 9 |
| 5 | 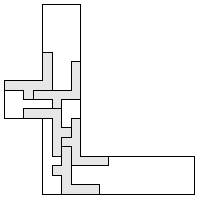 (and 9 others) (and 9 others) | 9 |
| 4 | 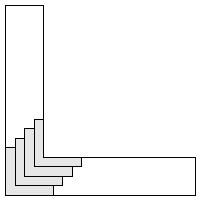 (and 10 others) (and 10 others) | 9 |
| 3 | 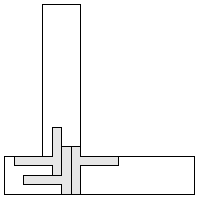 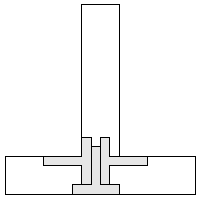 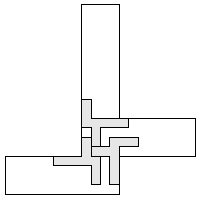 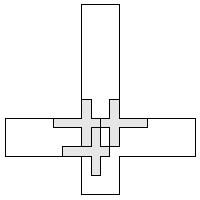 | 9 |
| 2 |  | 9 |
| 1 | 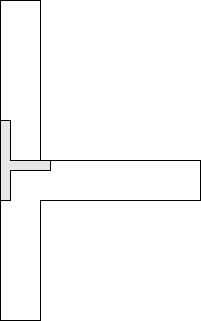 (George Sicherman) | 12 |
| 0 | 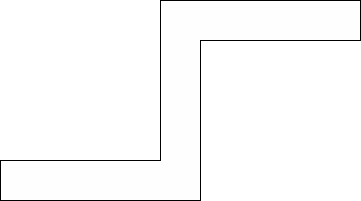 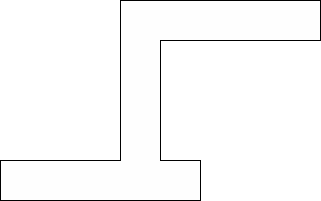 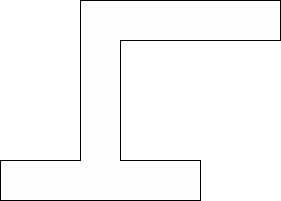 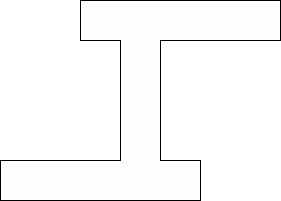 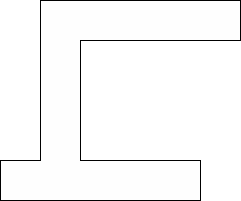 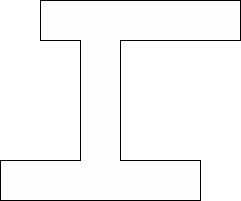 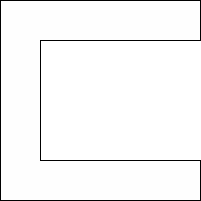 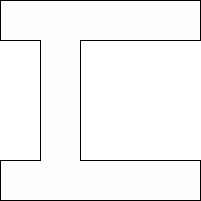 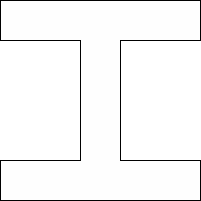 (George Sicherman) | 13 |
| Copies | Smallest | Area | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16 |  | 1 | |||||||||||||||||||||||||||||||||||||||||||||
| 15 | ? | ?
| 14 | ? | ?
| 13 | ? | ?
| 12 | 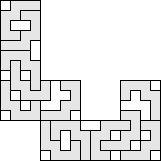 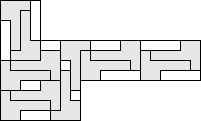 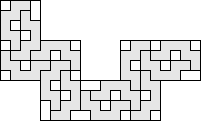 (George Sicherman) 8
| 11 | 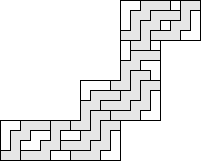 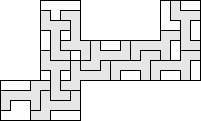 (George Sicherman) 8
| 10 | 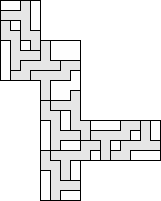 (George Sicherman) 8
| 9 | 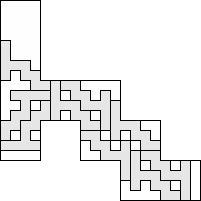 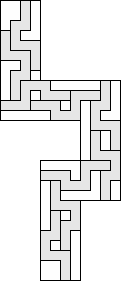 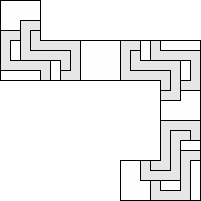 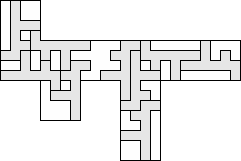 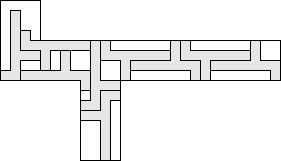 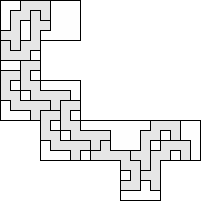 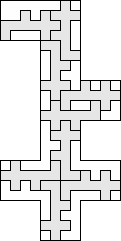 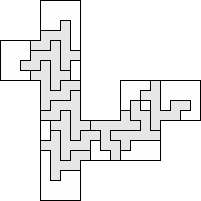 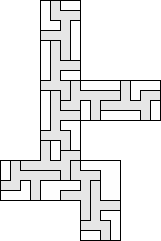 (George Sicherman) 9
| 8 | 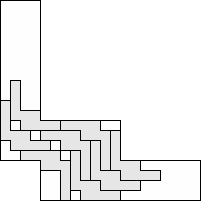 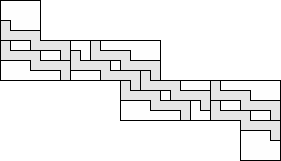 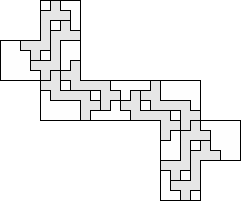 (George Sicherman) 10
| 7 | 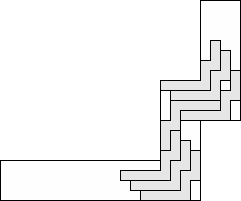 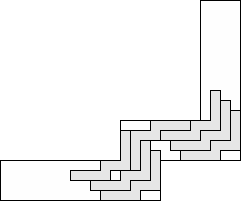 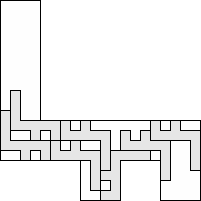 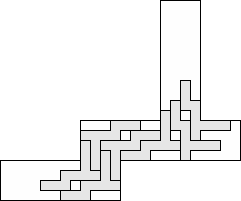 (George Sicherman) 10
| 6 | 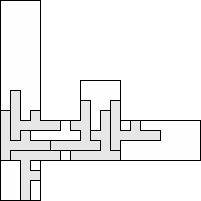 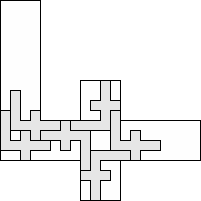 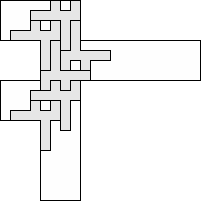 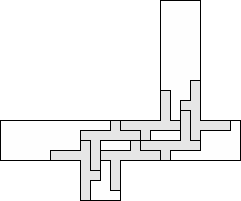 (George Sicherman) 10
| 5 | 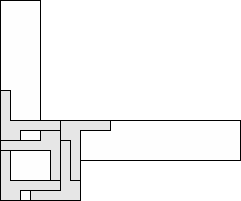 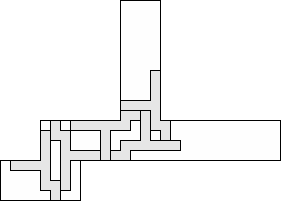 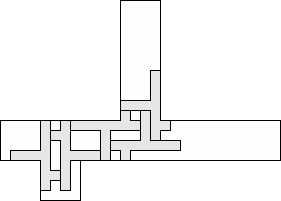 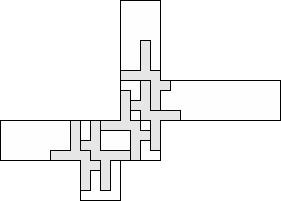 (George Sicherman) 11
| 4 |  9
| 3 | 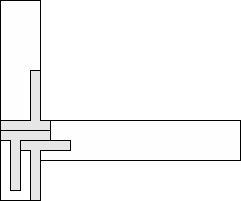 (George Sicherman) 10
| 2 | 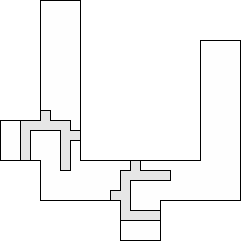 (and 61 others) (and 61 others)(George Sicherman) 14
| 1 | 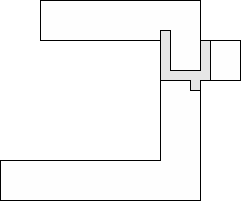 (George Sicherman) 13
| 0 |          (George Sicherman) 13
| |
| Copies | Smallest | Area | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 |  | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | ? | ?
| 23 | ? | ?
| 22 | 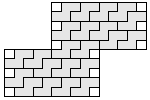 4
| 21 | ? | ?
| 20 | 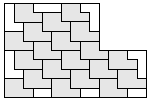 5
| 19 | 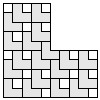 3
| 18 | 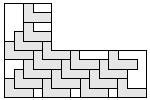 4
| 17 | 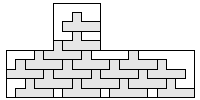 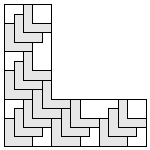  5
| 16 | 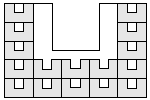 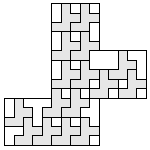 5
| 15 | 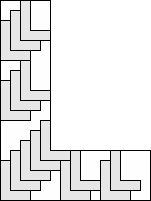 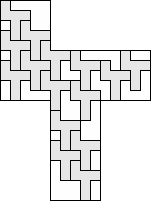 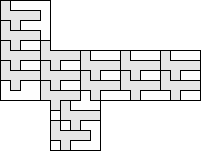 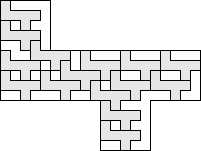 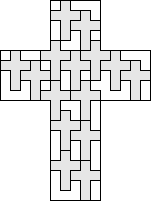 (George Sicherman) 6
| 14 | 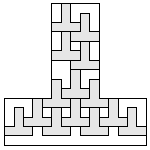 5
| 13 | 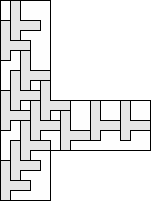 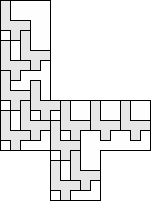 (George Sicherman) 6
| 12 | 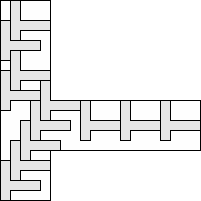 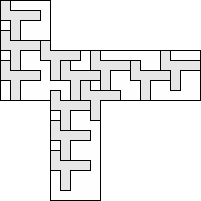 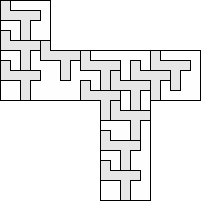 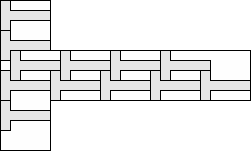 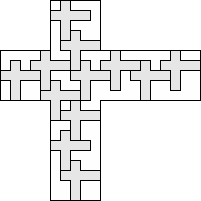 (George Sicherman) 7
| 11 | 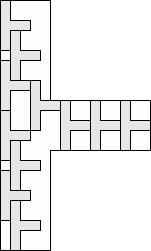 (George Sicherman) 7
| 10 | 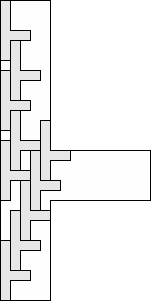 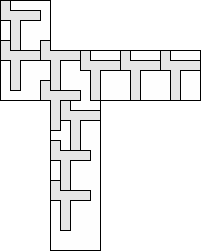 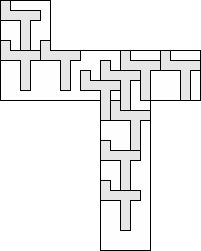 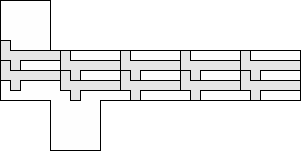 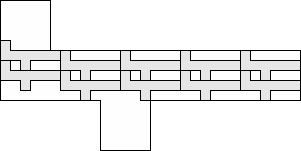 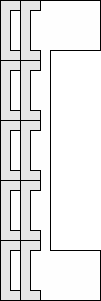 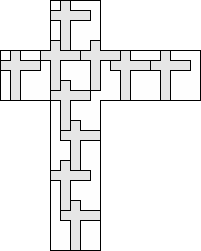 (George Sicherman) 8
| 9 | 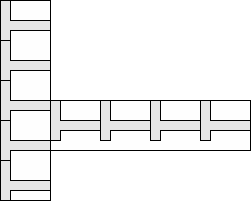 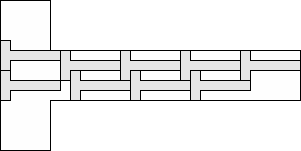 (George Sicherman) 8
| 8 | 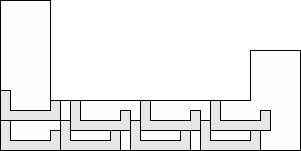 (and 13 others) (and 13 others)(George Sicherman) 9
| 7 | 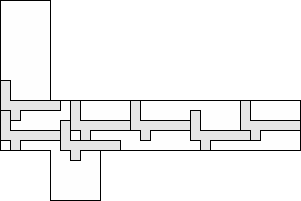 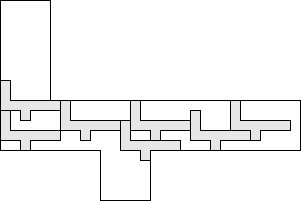 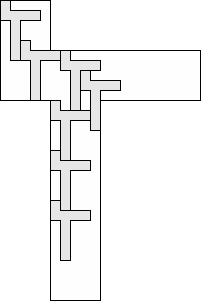 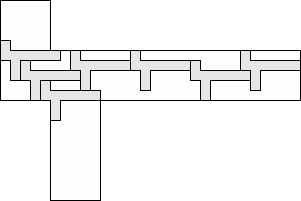 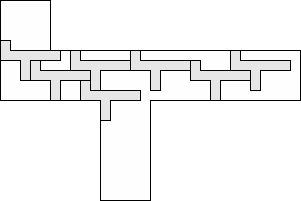 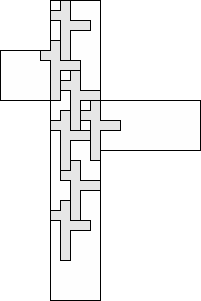 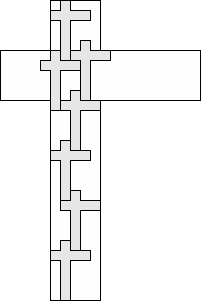 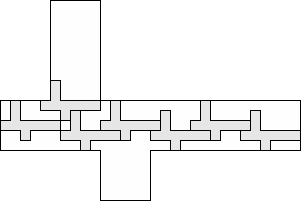 (George Sicherman) 9
| 6 |  (George Sicherman) 9
| 5 | 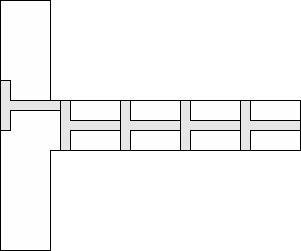 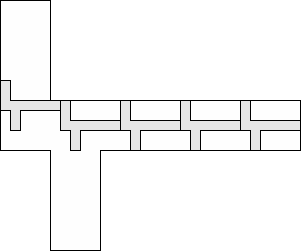 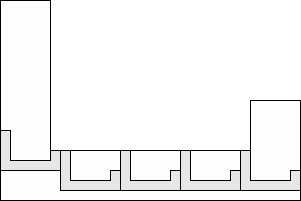 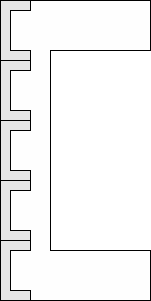 (George Sicherman) 10
| 4 | 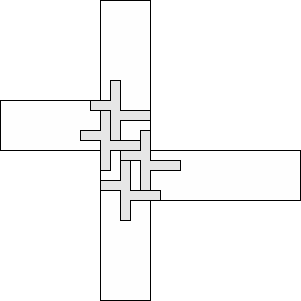 (and 20 others) (and 20 others)(George Sicherman) 11
| 3 | 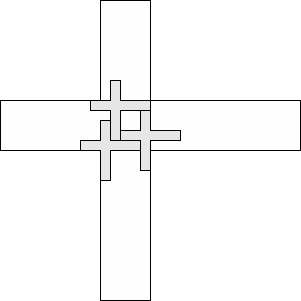 (and 14 others) (and 14 others)(George Sicherman) 11
| 2 | 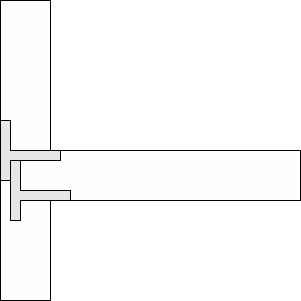 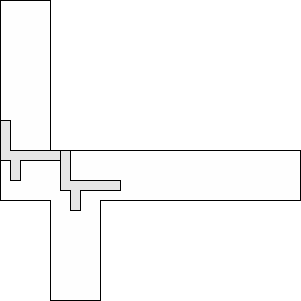 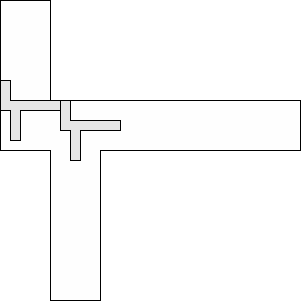 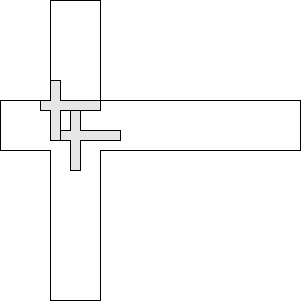 (George Sicherman) 11
| 1 | 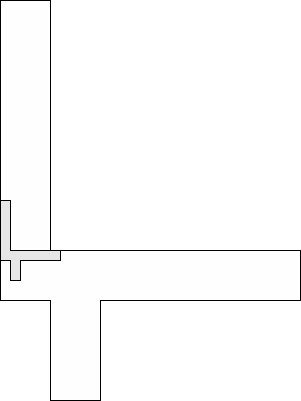 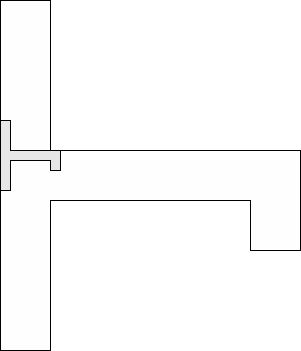 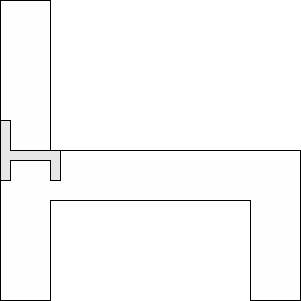 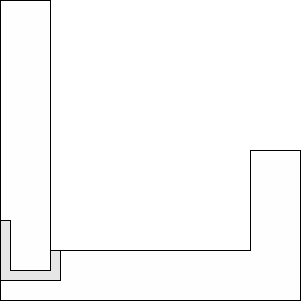 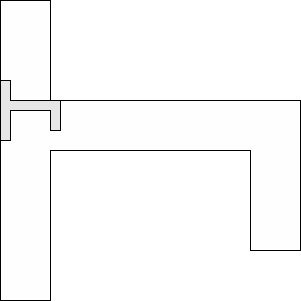 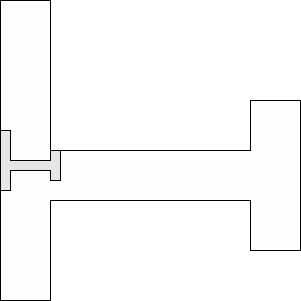 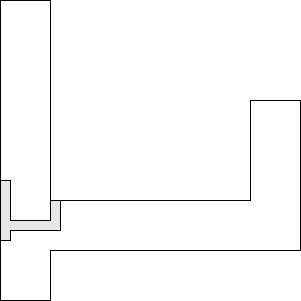 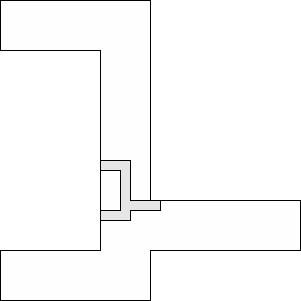 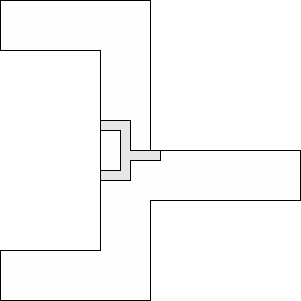 (George Sicherman) 13
| 0 | ? | ?
| |
| Copies | Smallest | Area | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 |  | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | ? | ?
| 23 | ? | ?
| 22 |  4
| 21 | ? | ?
| 20 | ? | ?
| 19 | ? | ?
| 18 | ? | ?
| 17 |  5
| 16 | ? | ?
| 15 | ? | ?
| 14 | 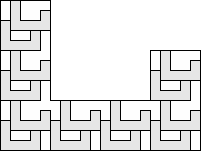 (George Sicherman) 7
| 13 | ? | ?
| 12 | ? | ?
| 11 | ? | ?
| 10 | ? | ?
| 9 | ? | ?
| 8 | ? | ?
| 7 | ? | ?
| 6 | ? | ?
| 5 | ? | ?
| 4 | ? | ?
| 3 | ? | ?
| 2 | ? | ?
| 1 | ? | ?
| 0 | ? | ? | |
| Copies | Smallest | Area |
|---|---|---|
| 4 |  | 1 |
| 3 | 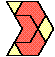 | 4 |
| 2 |  | 6 |
| 1 | 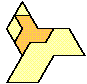 | 7 |
| 0 | 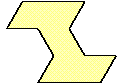 | 10 |
| Copies | Smallest | Area |
|---|---|---|
| 9 | 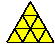 | 1 |
| 8 | 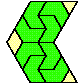 | 4 |
| 7 | 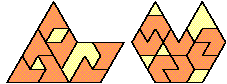 | 5 |
| 6 | 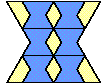 | 6 |
| 5 | 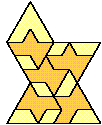 | 7 |
| 4 |  | 8 |
| 3 | 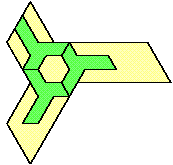 | 10 |
| 2 | 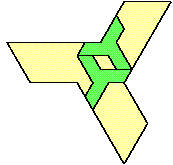 | 10 |
| 1 | 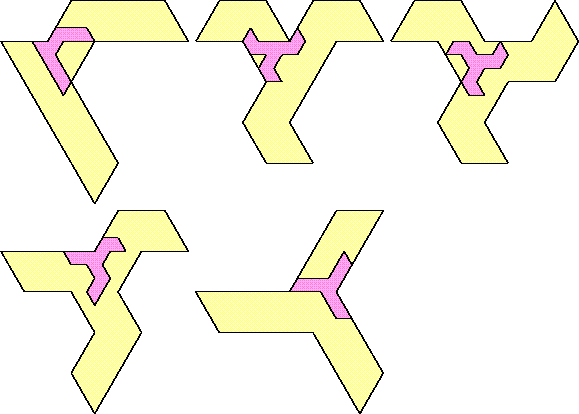 | 13 |
| 0 | 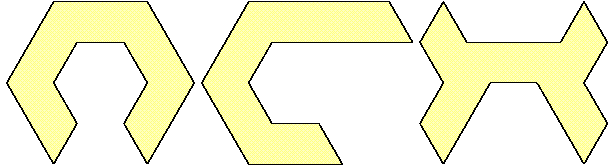 | 15 |
| Copies | Smallest | Area |
|---|---|---|
| 16 |  | 1 |
| 15 |  | 4 |
| 14 | 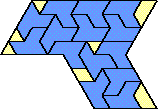 | 6 |
| 13 | 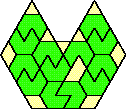 | 5 |
| 12 | 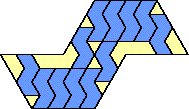 | 6 |
| 11 |  | 7 |
| 10 | 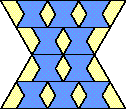 | 6 |
| 9 |  (and 12 others) (and 12 others) | 10 |
| 8 |  | 10 |
| 7 |  | 12 |
| 6 | 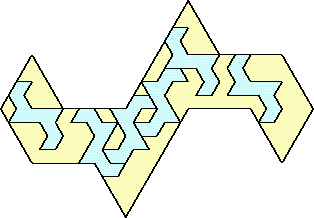 (and 18 others) (and 18 others) | 14 |
| 5 | 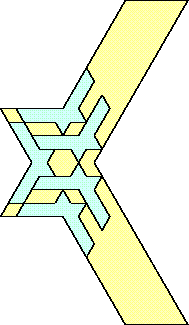 (and 24 others) (and 24 others) | 14 |
| 4 | 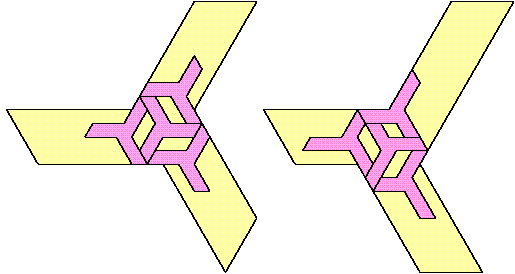 | 13 |
| 3 | 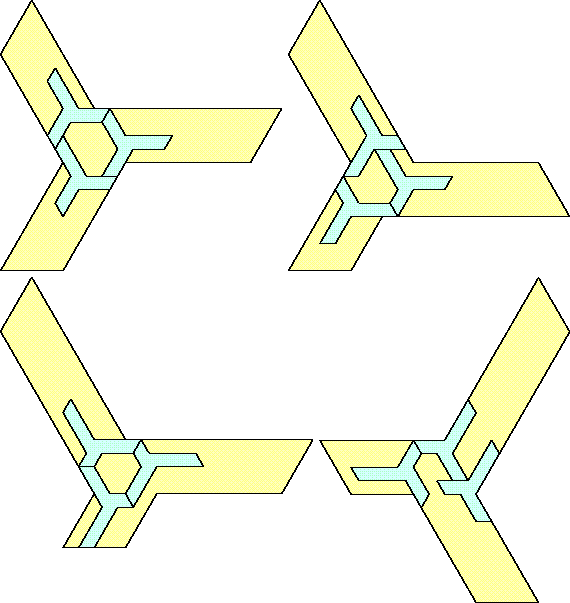 | 14 |
| 2 | 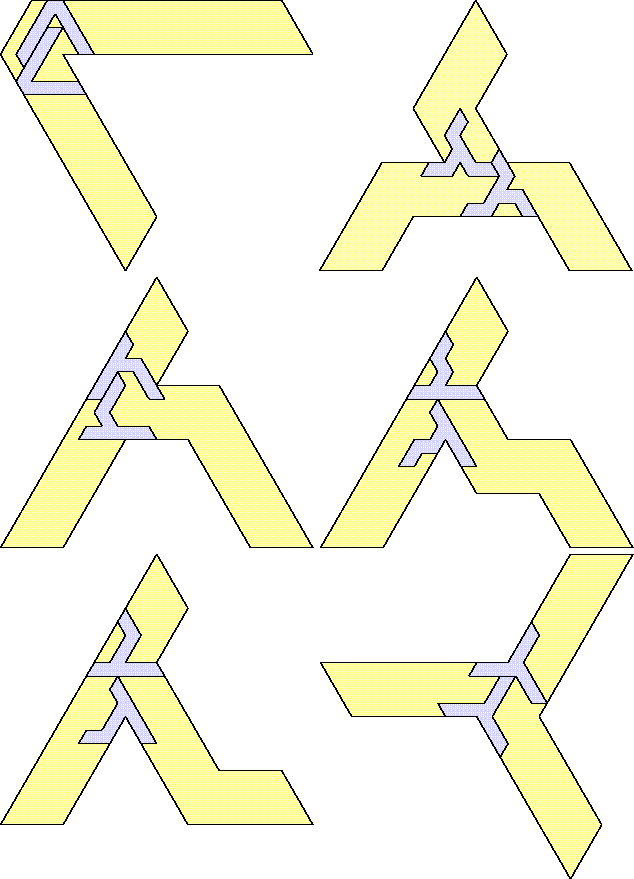 | 16 |
| 1 | 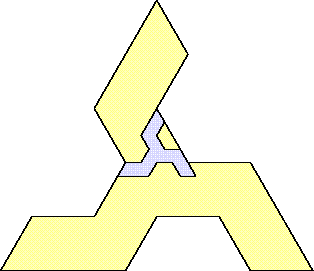 | 16 |
| 0 | 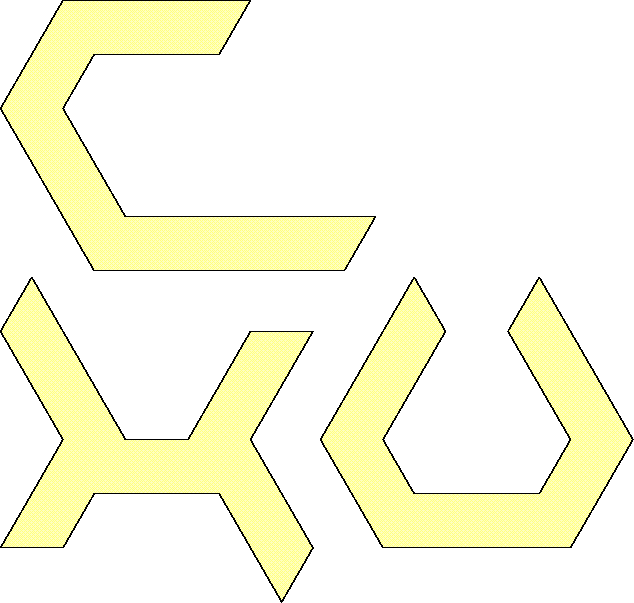 | 21 |
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 2/17/08.