Problem of the Month (April 2013)

Say we have a chessboard filled with white chess pieces and a cyclical order in which the pieces are to be moved. In turn, we move each piece as far as it can be moved (measured in number of squares), as long as that square is unique. (If no move is possible, or the longest move is not unique, we stop.) Some positions eventually repeat themselves. It is not hard to find positions where each piece moves only twice each period, or crowded positions where the pieces have to cycle around. It is harder to find more interesting examples.

What positions can you find that repeat? What periods are possible with a given number of pieces? What are the smallest boards (in terms of area) that accomplish this? Positions like this that contain kings and knights are harder to find, because of all of their moves are the same length. What positions using kings or knights can you find? What periods are possible with those pieces? What combinations of pieces have repeating positions?

ANSWERS

Here are the known periods 7 or fewer pieces, on the smallest-known boards:

1 Piece:
period 2

2 Pieces: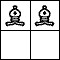
period 4

3 Pieces:
period 4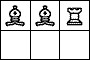
period 6
period 10
period 12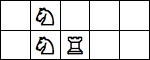
period 18 (Andrew Bayly)

4 Pieces: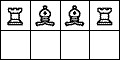
period 8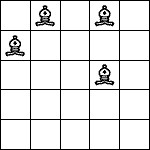
period 12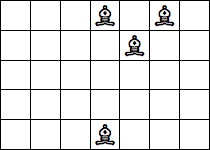
period 14 (Joe DeVincentis)
period 16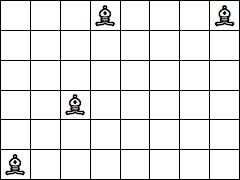
period 20 (Joe DeVincentis)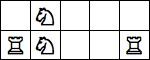
period 24 (Andrew Bayly)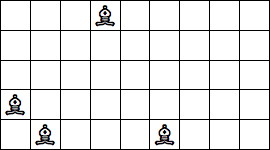
period 40 (Joe DeVincentis)

5 Pieces:
period 6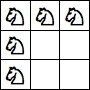
period 8
(Jon Palin)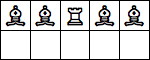
period 10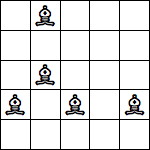
period 12 (Jon Palin)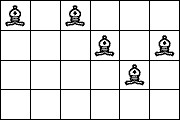
period 16
period 20
period 30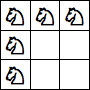
period 40
(George Sicherman)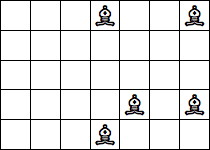
period 70 (Joe DeVincentis)

6 Pieces:
period 8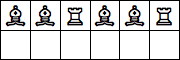
period 12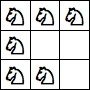
period 16 (Andrew Bayly)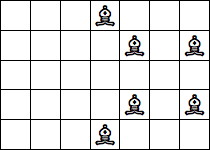
period 20 (Joe DeVincentis)
period 24

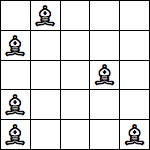period 36 (Jon Palin)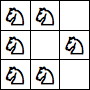
period 48 (Jon Palin)
period 72 (Jon Palin)
period 84 (Joe DeVincentis)
period 96 (Andrew Bayly)

7 Pieces:
period 8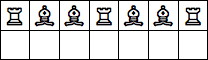
period 14
period 28 (Jon Palin)
period 56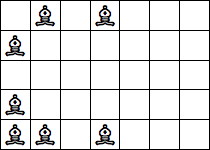
period 70 (Joe DeVincentis)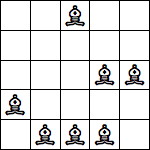
period 84 (Andrew Bayly)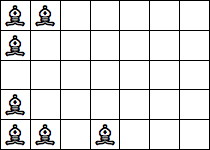
period 98 (Joe DeVincentis)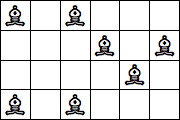
period 112 (Andrew Bayly)

All the known periods are even. Bryce Herdt asks whether there are any odd periods.

Here are the known periods using 3 or fewer pieces:

Pieces Period Rectangles
2 n×m, m≤3n-4
2 1×2
2 2×3, 2×4, 2×5
2 m×n, except 1×1 and 2×2 (JD)
2 m×n, except 1×1 and 2×2 (JD)
4 n×m, n≤m≤3n-4
none
4 2×3, 2×4
4 n×m, n≤m≤3n-4
4 n×m, n≤m≤3n-4
none
none
none
none
4 2×3, 2×4, 2×5
4 2×4, 2×5, 2×6
4 2×4, 2×5, 2×6
4 m×n, 2≤m≤n, except 2×2 (JD)
4 m×n, 2≤m≤n, except 2×2 (JD)
4 m×n, 2≤m≤n, except 2×2 (JD)

Pieces Period Rectangles
4
6
10 (2n+1)×(2n+1), except 1×1
3×4, n×m, 4≤n≤m≤3n-5 (JD)
n×(3n-6), n≥5 (JD)
none
6 2×3 (JP)
6 n×m, 3≤n≤m≤4n-4 (JD)
6
12 2×3, n×m, 3≤n≤m≤4n-4 (JD)
4≤n≤m≤3n-5 (JD)
none
none
none
none
6 2×4 (JP)
6 3×3 (JP), 2×5, 2×6 (JD)
6 2×5 (JP), 3×3 (AB), 2×4, 2×6 (JD)
6 3×3, 3×5, 3×6, n×m, 4≤n≤m≤3n-2 (JD)
6
12 3×3, 3×5, 3×6, n×m, 4≤n≤m≤4n-5 (JD)
7≤n≤m≤2n-6 (JD)
6
12 3×3, 3×5, 3×6, n×m, 4≤n≤m≤4n-5 (JD)
7≤n≤m≤2n-6 (JD)

Pieces Period Rectangles
4 2×2
none
12 2×2
12 2×2
none
none
none
12 2×2
12 2×2
12 2×2
6 2×4 (JP)
6
18 2×6, 2×7, 2×8 (JD)
2×5
6
18 2×3, 2×4, 2×5 (JP), 2×6, 2×7, 2×8 (JD)
2×5
6 3×3 (JP)
6
12 3×3 (JD)
2×6 (JD)
12 2×6 (JD)
4
6
10 n×m, 2≤n≤m≤3n-4 (JD)
n×m, 3≤n≤m (AB)
2×n, n≥4 (JD)
6
12 n×m, 3≤n≤m (AB), 2×n, n≥4 (JD)
n×n, except 1×1
6
12 n×m, 3≤n≤m (AB), 2×n, n≥4 (JD)
n×n, except 1×1
4
6 n×n, except 1×1
n×m, 3≤n≤m (AB), 2×n, n≥4 (JD)

JP = Jon Palin
JD = Joe DeVincentis
AB = Andrew Bayly

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 4/18/13.