Problem of the Month (May 2004)

A popular type of number puzzle involves placing the digits 1 through 9 into a 3×3 square grid containing some arithmetic operations so that each row and column gives some correct equation. This month we look into the existence of digit isogrids, rectangular puzzle grids using the operations + – × / ^ and the first n positive integers that have the same result in every row and column. Every pair of digits must be separated by an operation, and all operations are performed "left to right" or "top down".

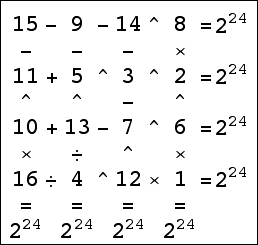
An 3×3 isogrid for 15 exists using only addition: the standard 3×3 magic square. There are 3×3 isogrids for 1, 2, 3, 5, 11, 13, and 18 that use only two different operations. Can you find them? There are 3×3 isogrids for 4, 6-10, 12, 14, 16, 20, and 48 using only 3 operations. The 3×3 isogrid for 36 requires 4 operations. Can you find them?

What results are possible with different sized isogrids? Can you find the possible results in a 2×n isogrid in general? I'm particularly interested in possible results of a 4×4 isogrid. In higher dimensions, what is the smallest isobox?

ANSWERS

Guy Segal found a 2×4 isogrid, and used it to prove the existence of 2×n isogrids for every n≥4.

Jordan Balla found a 3×3 isogrid with result 16.

Bill Clagett found all the possible isogrids for the 2×3, 2×4, 3×3, 3×4, and 4×4 cases, including negative and fractional results. Here are his results:

Size	Possible Integer Results of Isogrids	Possible Fractional Results of Isogrids
2×3	–1, [1,3], 7
2×4	–4, –2, –1, [1,4], 9
3×3	–10, –8, [–6,–1], [1,16], 18, 20, 36, 48
3×4	–18, –16, –14, [–12,30], 32, 33, 36, 40, 44, 48, 56, 60	1/2, 3/2, 5/2
4×4	–80, –72, –64, –60, –56, –48, –45, –42, –40, –36, –35, [–33,138], 140, 141, [143,145], 147, 150, [152,154], 156, 157, [159,162], 165, [168,170], 174, 176, 180, 182, 189, 192, 196, 198, 200, 208, 210, 216, 220, 224, 225, 234, 240, 243, 252, 256, 264, 270, 288, 336, 360, 420, 480, 512, 4096, 16777216	–21/2, –15/2, –11/2, –9/2, –7/2, –5/2, –3/2, –3/4, –2/3, –1/2, –1/3, –1/4, 1/6, 1/4, 1/3, 1/2, 2/3, 3/4, 5/4, 4/3, 3/2, 5/3, 7/4, 9/4, 7/3, 5/2, 8/3, 10/3, 7/2, 11/3, 13/3, 9/2, 14/3, 16/3, 11/2, 13/2, 22/3, 15/2, 17/2, 26/3, 28/3, 19/2, 21/2, 32/3, 34/3, 23/2, 25/2, 27/2, 29/2, 31/2, 33/2, 52/3, 35/2, 39/2

This is his amazing 4×4 isogrid with result 2²⁴=16777216:

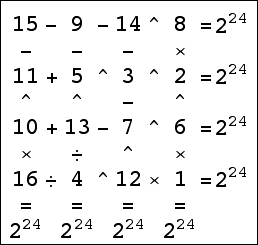
Bill Clagett also noted that there are arrays of numbers which give several different isogrids results depending on the operations inserted. He wondered whether the 3×4 example he found was the smallest one.

Bill Clagett also showed there is a unique 3×3×2 isobox. Below are the two layers. All the signs between the two layers are "–" except for one "^", and all the results are equal to 1.

    top layer:
    1 ^ 18 ^  5
    ^    -    +
   16 -  7 /  9
    ^    /    -
    3 + 11 - 13

   bottom layer:
   14 - 17 +  4
    -    -    +
   15 -  6 -  8
    ^    -    /
    2 + 10 / 12

Philippe Fondanaiche found all the 3×3 isogrid results. He also showed that for 2×n isogrids, where n≤7, that the results 1-n and 2n+1 were possible. He couldn't extend this to n=8 though, since he couldn't find results of 5 or 6. Can anyone verify this?

Philippe Fondanaiche also found results of 0-34 for 4×4 isogrids using only addition and subtraction.

Here are the small isogrids:

2×3 Isogrids

2×4 Isogrids

3×3 Isogrids





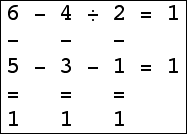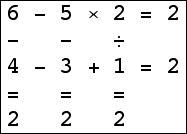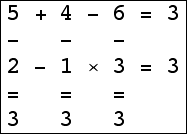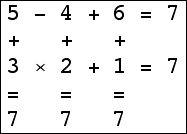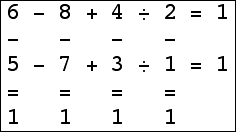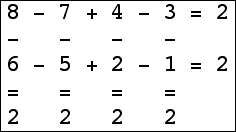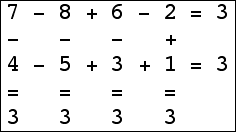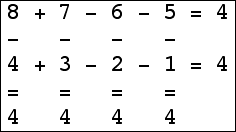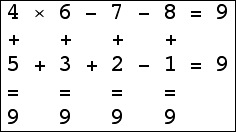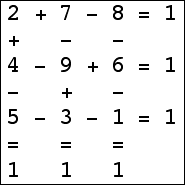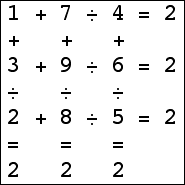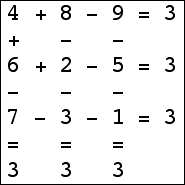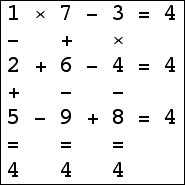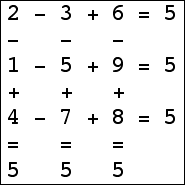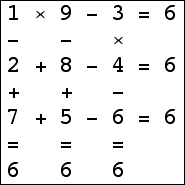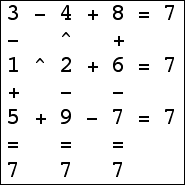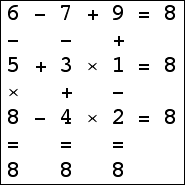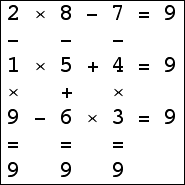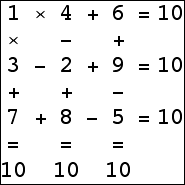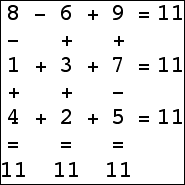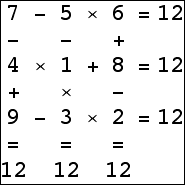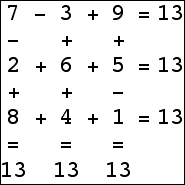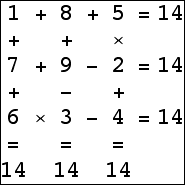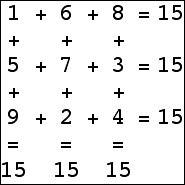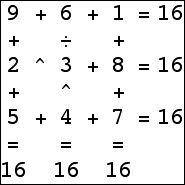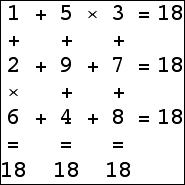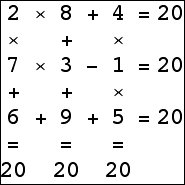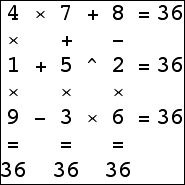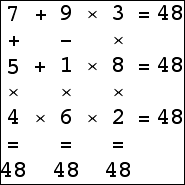			(Bryce Herdt)

I investigated 2×n isogrids. It turns out results of 2n+1 and some numbers in [1,n] are possible, and nothing in [n,2n] is possible. The following graph shows what exists. the rows indicate n=3 (top) through n=28 (bottom), and the black squares indicate the numbers between 1 and n which are 2×n isogrids.

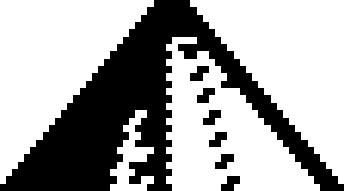
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 5/25/04.