Problem of the Month (May 2007)
Pick a polyomino. Arrange as few copies as possible in a square so that the same number of squares in every row and column are covered.
What are the best results for small polyominoes? hexominoes? heptominoes? What patterns can you find? Which polyominoes are impossible? If we relax the requirements, what is the smallest rectangle containing copies of a polyomino so that the same number of squares in each column are covered? What are the solutions for polyhexes or polyiamonds or other polyforms?
ANSWERS
To pack m copies of an n-omino into a square of side s with c squares covered in each row and column, Livio Zucca gave the trivial necessary condition n m = s c.
The orange figures were found by me. The green figures were found by George Sicherman.
Polyominoes, Row and Column
Small Polyominoes
Tetrominoes
Pentominoes
Hexominoes
Heptominoes
The Largest Octominoes
The missing n-ominoes are impossible for n≤6. Joseph DeVincentis and George Sicherman proved the Z pentomino was impossible. There are 5 unsolved cases for n=7: 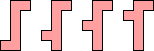 . The unsolved cases for n=8 are shown in shown below.
. The unsolved cases for n=8 are shown in shown below.
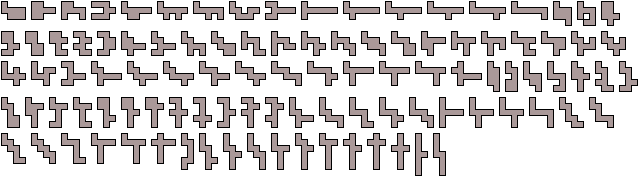
In 2018, George Sicherman considered one-sided polyominoes, and found these solutions that differed from the two-sided case:
One-Sided, Row and Column
Pentomino 24

| Hexomino 24

|
|
Polyominoes, Column
Small Polyominoes
Pentominoes
Hexominoes
George Sicherman proved that if a polyomino has an orientation where the first few columns all contain a squares, and the rest of the columns all contain b squares, the polyomino has a one-way solution. He conjectures that if a polyomino has a monotone shadow in some direction, the polyomino has a one-way solution.
Polyiamonds, Row and One Column
Small Polyiamonds
Pentiamonds
Hexiamonds
Heptiamonds
Polyiamonds, One Column
Small Polyiamonds
Hexiamonds
Heptiamonds
Polyhexes, Row and One Column
Small Polyhexes
Tetrahexes
Pentahexes
Hexahexes
The missing polyhexes are impossible.
Polyhexes, One Column
Small Polyhexes
Pentahexes
Polykings, Row and Column
Small Polykings
Tetrakings
If you can extend any of these results, please
e-mail me.
Click here to go back to Math Magic. Last updated 5/30/07.



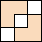
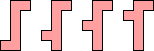 . The unsolved cases for n=8 are shown in shown below.
. The unsolved cases for n=8 are shown in shown below.