Problem of the Month (May 2008)
Let n < m be positive integers. What is the largest shape with the property that n of them can be packed inside a square of area n, and m of them can be packed inside a square of area m ? Can you beat any of the results below?
ANSWERS
Jeremy Galvagni noticed that if m=(a/b)2n, then area 1 could be trivially covered. He also showed that when n=m–k, that area √(1–k/m) can be covered using thin rectangles:

He later improved this bound to area 2√(m/n) + 3√(n/m) – 4 when n is even, and √(n/m) + 2n√(n/m)/(n+1) + 2√(mn)/(n+1) – 4n/(n+1) when n is odd.
Joe DeVincentis noticed that if k is the smallest square number greater than n, then we can use n of k squares, for a fill fraction of n/k > n/(n+2√n) → 1 as n → ∞.
Here are the best known solutions, together with the proportion of the area covered. Click on the pictures for the figures of n regions in squares of area n.
n=1
m=2
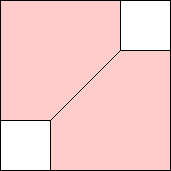
2√2 – 2 = .828+
| m=3

(2√3 + 3) / 8 = .808+
(Gavin Theobald)
| m=4

1
| m=5
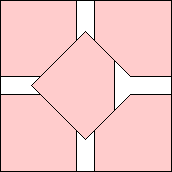
.889+
|
m=6
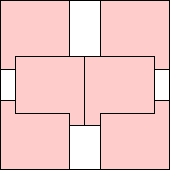
7/√6 – 2 = .857+
(Gavin Theobald)
| m=7
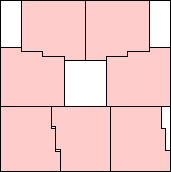
(25√7 – 49) / 20 = .857+
(Gavin Theobald)
| m=8

√2 – 1/2 = .914+
| m=9

1
|
m=10
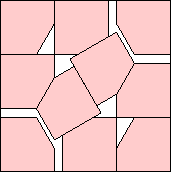
.906+
(Gavin Theobald)
| m=11

2√11 – 23/4 = .883+
(Gavin Theobald)
| m=12
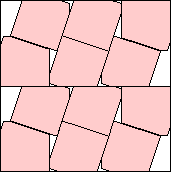
.897+
(Gavin Theobald)
| m=13
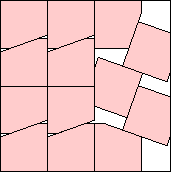
.892+
(Gavin Theobald)
|
m=14
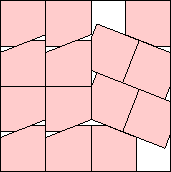
.913+
(Gavin Theobald)
| m=15

.937+
(Gavin Theobald)
| m=16

1
| |
n=2
m=3

2√3 – 5/2 = .964+
| m=4

1
| m=5
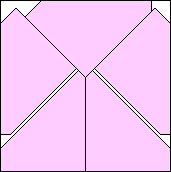
.948+
(Gavin Theobald)
| m=6

(51 - 26√3)/6 = .994+
(Gavin Theobald)
|
m=7
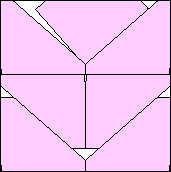
.969+
(Gavin Theobald)
| m=8

1
| m=9
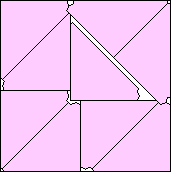
.973+
(Gavin Theobald)
| m=10
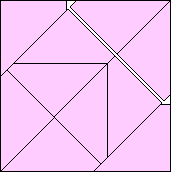
√10 + √5 - √2 - 3 = .984+
(Maurizio Morandi)
|
m=11
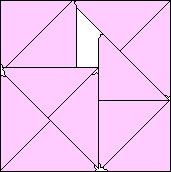
.957+
(Gavin Theobald)
| m=12
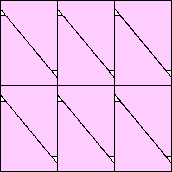
(36 - 5√6)/24 = 0.989+
(Maurizio Morandi)
| m=13
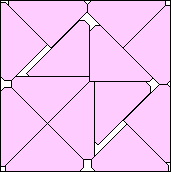
.963+
(Gavin Theobald)
| m=14
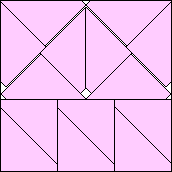
.986+
(Maurizio Morandi)
|
m=15

.978+
(Gavin Theobald)
| m=16

1
| |
n=3
m=4
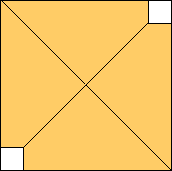
2√3 – 5/2 = .964+
| m=5
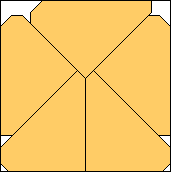
.960+
(Gavin Theobald)
| m=6
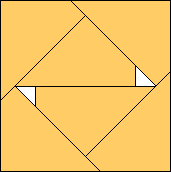
6√2 – 15/2 = .985+
(Gavin Theobald)
| m=7
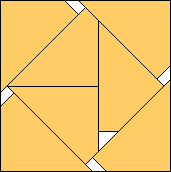
(224√2 – 35) / 289 = .975+
(Gavin Theobald)
|
m=8
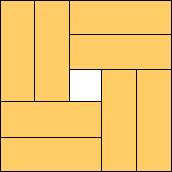
(2√6 – 2) / 3 = .966+
| m=9
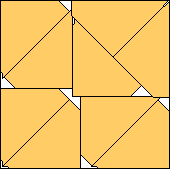
.974+
(Gavin Theobald)
| m=10
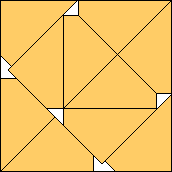
.975+
(Maurizio Morandi)
| m=11
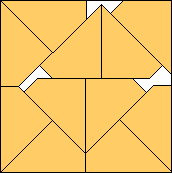
.961+
(Maurizio Morandi)
|
m=12

1
| m=13
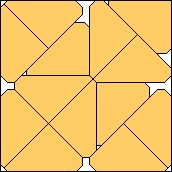
.964+
(Maurizio Morandi)
| m=14
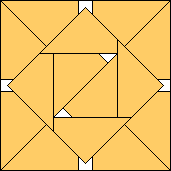
(224√2 – 35) / 289 = .975+
(Gavin Theobald)
| m=15
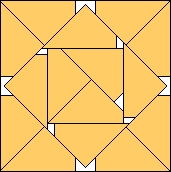
.966+
(Gavin Theobald)
|
m=16
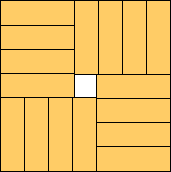
√3 – 3/4 = .982+
(Gavin Theobald)
| |
n=4
m=5
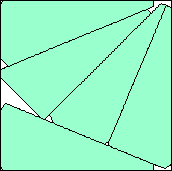
.974+
(Maurizio Morandi)
| m=6
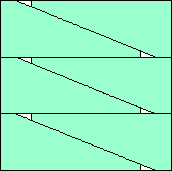
(36 – 5√6) / 24 = .989+
(Maurizio Morandi)
| m=7
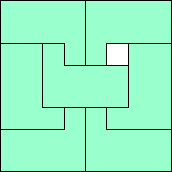
63/64 = .984+
(Joe DeVincentis)
| m=8
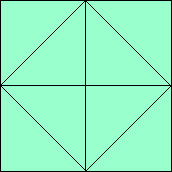
1
|
m=9
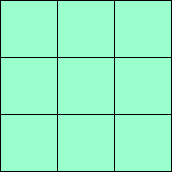
1
| m=10
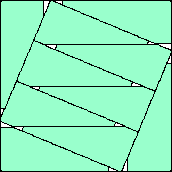
.986+
(Maurizio Morandi)
| m=11
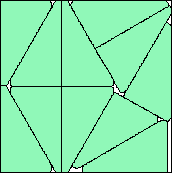
.981+
(Maurizio Morandi)
| m=12
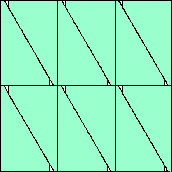
(36 - 7√3)/24 = .994+
(Maurizio Morandi)
|
m=13
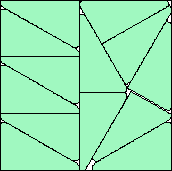
.985+
(Maurizio Morandi)
| m=14
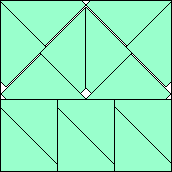
.986+
(Maurizio Morandi)
| m=15
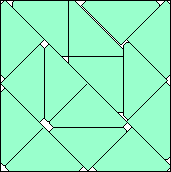
.978+
(Gavin Theobald)
| m=16
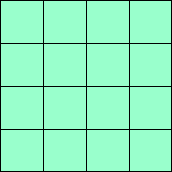
1
| |
n=5
m=6
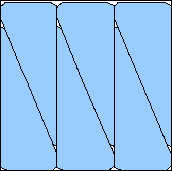
.973+
(Maurizio Morandi)
| m=7
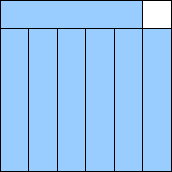
35/36 = .972+
| m=8
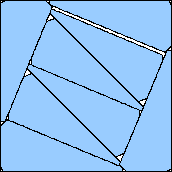
.975+
(Maurizio Morandi)
| m=9
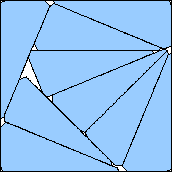
.977+
(Maurizio Morandi)
|
m=10

.974+
(Maurizio Morandi)
| m=11
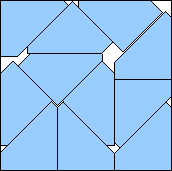
.9618+
(Maurizio Morandi)
| m=12
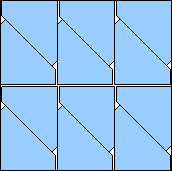
.965+
(Maurizio Morandi)
| m=13
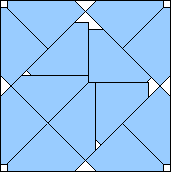
.964+
(Gavin Theobald)
|
m=14
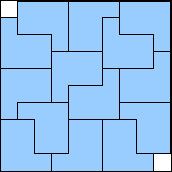
35/36 = .972+
| m=15
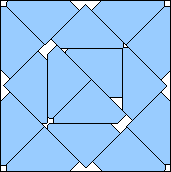
.954+
(Gavin Theobald)
| m=16
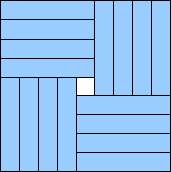
(4√5 – 4)/5 = .988+
(Gavin Theobald)
| |
If you can extend any of these results, please
e-mail me.
Click here to go back to Math Magic. Last updated 12/16/09.

