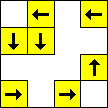
period 4
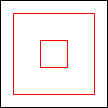
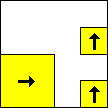
period 12

(Berend van
der Zwaag)
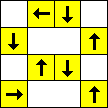
period 2

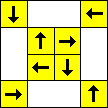
period 2
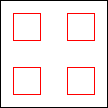
What sort of periodic behaviors are possible? What if we allow rectangular blocks as well?
Here are some small block configurations with more than one block, their periods, and the paths that the centers of the blocks take. You can click on a configurations to see an animation.
 period 4  |  period 12  (Berend van der Zwaag) |  period 2  |  period 2  |
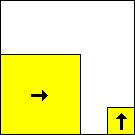 period 48 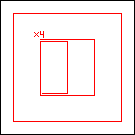 | 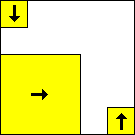 period 16 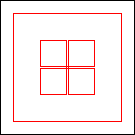 | 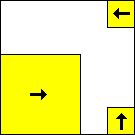 period 16 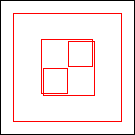 | 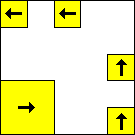 period 16  | 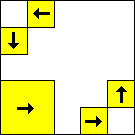 period 8  | 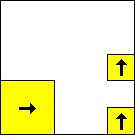 period 32  (Berend van der Zwaag) | 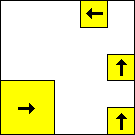 period 48 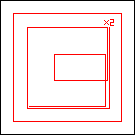 (Berend van der Zwaag) | 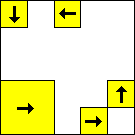 period 16 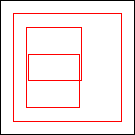 (Berend van der Zwaag) | 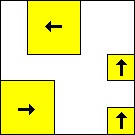 period 16  (Berend van der Zwaag) |
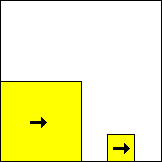 period 100 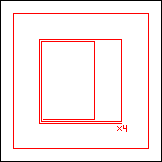
| 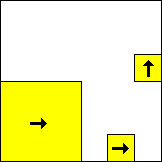 period 20 
| 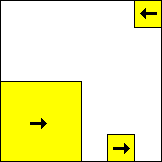 period 20 
| 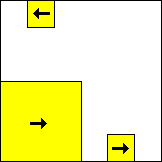 period 10 
| 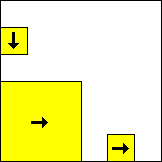 period 20 
| 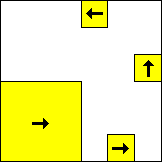 period 60 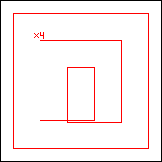
| 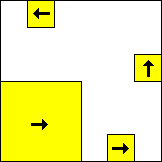 period 60 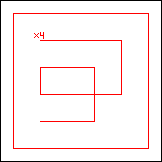
|
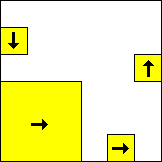 period 60 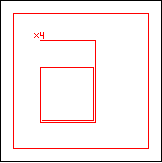 | 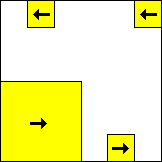 period 60 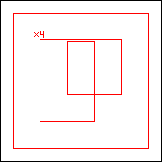 | 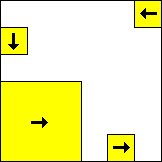 period 60 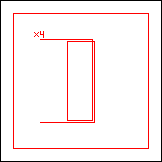 | 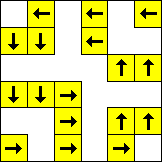 period 4  | 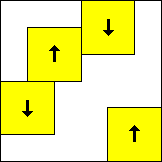 period 4 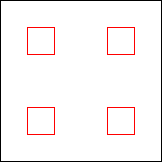 | 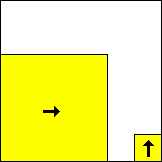 period 20  (Berend van der Zwaag) | 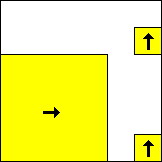 period 20 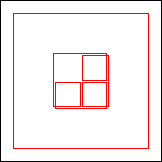 (Berend van der Zwaag) |
Here are some configurations using rectangular blocks.
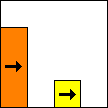 period 36 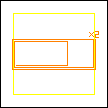 | 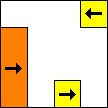 period 12 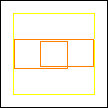 | 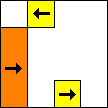 period 6  | 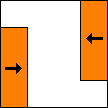 period 4 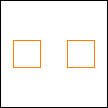 | 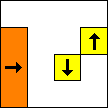 period 4 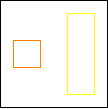 (Berend van der Zwaag) | 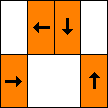 period 3 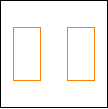 (Berend van der Zwaag) | 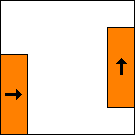 period 14 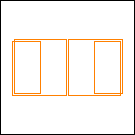 (Berend van der Zwaag) | 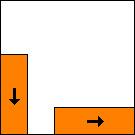 period 24 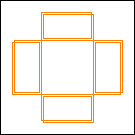 (Berend van der Zwaag) |
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 5/22/09.