Problem of the Month (May 2015)
Suppose there are n points in a unit square. We start at one, move straight to the closest point, then straight to the closest point not yet visited, and so on, until you return to the initial point. How long can your cycle be? How do the answers change for a unit equilateral triangle, or a circle with unit diameter? Thanks to Stan Wagon for making me aware of this problem, first investigated by Al Zimmermann.
ANSWERS
Solutions were received from Al Zimmermann, Mike Elgersma, Maurizio Morandi, Johannes Waldmann, and Rob Pratt.
Here are the best known answers:
Longest Known Greedy Cycles for Squares
2
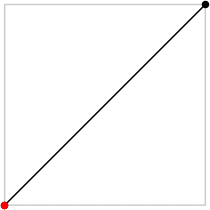
L = 2√2 = 2.828+
| 3
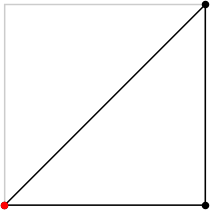
L = 2 + √2 = 3.414+
| 4
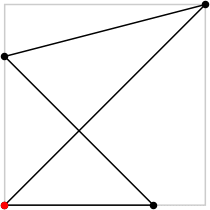
L = 2√6 + √3 – √2 – 1 = 4.216+
| 5
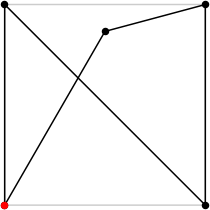
L = (6 + √2 + √6) / 2 = 4.931+
| 6
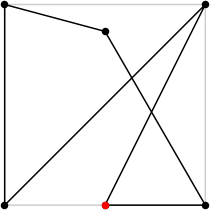
L = (5+√2+√5+√6) / 2 = 5.549+
(Al Zimmermann)
|
7
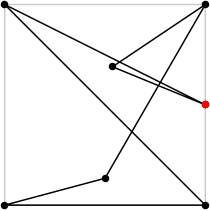
L = 6.106+
(Rob Pratt)
| 8
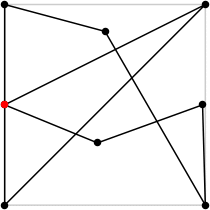
L = 6.607+
(Rob Pratt)
| 9
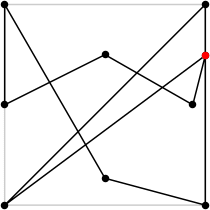
L = 6.996+
(Rob Pratt)
| 10
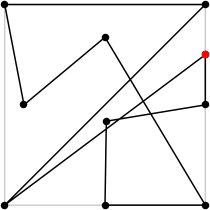
L = 7.342+
(Rob Pratt)
| 11
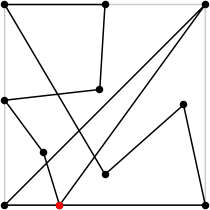
L = 7.668+
(Rob Pratt)
|
12
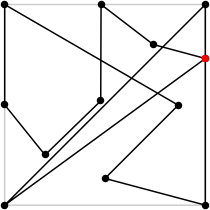
L = 7.971+
(Rob Pratt)
| 13
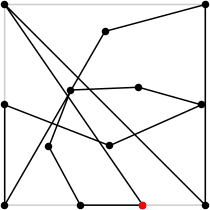
L = 8.316+
(Rob Pratt)
| 14
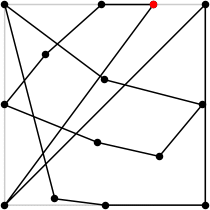
L = 8.641+
(Rob Pratt)
| 15
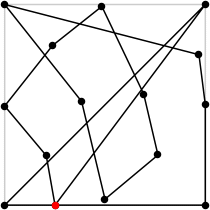
L = 8.944+
(Rob Pratt)
| 16
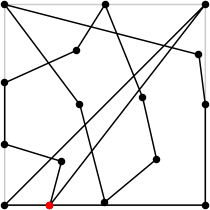
L = 9.193+
(Rob Pratt)
|
17
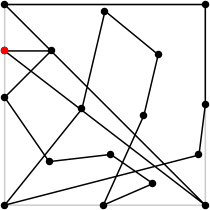
L = 9.471+
(Rob Pratt)
| 18
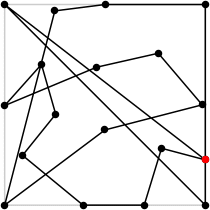
L = 9.719+
(Rob Pratt)
| 19
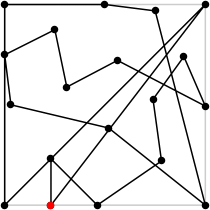
L = 9.934+
(Rob Pratt)
| 20
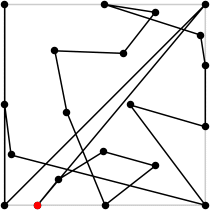
L = 10.123+
(Rob Pratt)
| 21
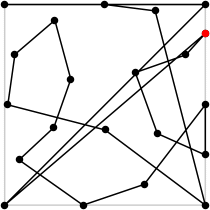
L = 10.379+
(Rob Pratt)
| |
Longest Known Greedy Cycles for Triangles
2
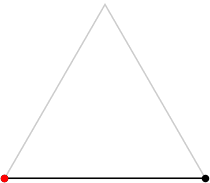
L = 2
| 3
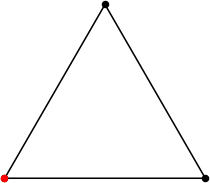
L = 3
| 4
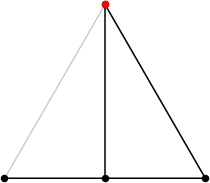
L = (5 + √3) / 2 = 3.366+
| 5
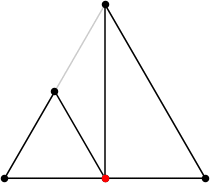
L = (6 + √3) / 2 = 3.866+
| 6
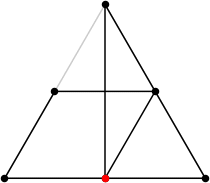
L = (7 + √3) / 2 = 4.366+
|
7
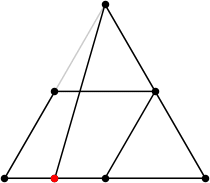
L = (15 + √13) / 4 = 4.651+
| 8
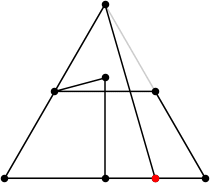
L = (15+√13+√6–√2)/4 = 4.910+
(Rob Pratt)
| 9
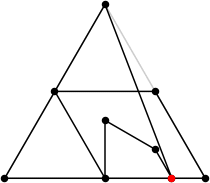
L = (22+√31+2√3)/6 = 5.171+
(Rob Pratt)
| 10
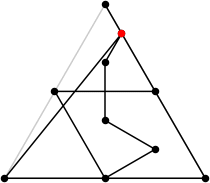
L = (22+√31+3√3)/6 = 5.460+
(Rob Pratt)
| 11
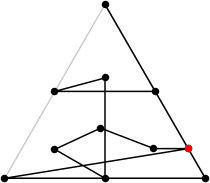
L = 5.680+
(Rob Pratt)
|
12
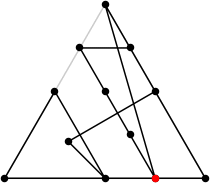
L = (19+√13+√6–√2)/4 = 5.910+
(Rob Pratt)
| 13
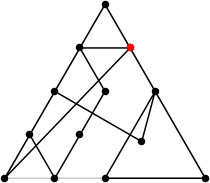
L = (20+√13+√6–√2)/4 = 6.160+
(Rob Pratt)
| 14
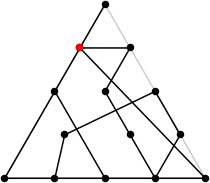
L = 6.373+
(Rob Pratt)
| 15
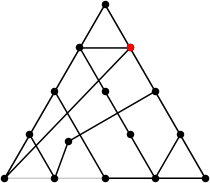
L = 6.596+
(Rob Pratt)
| 16
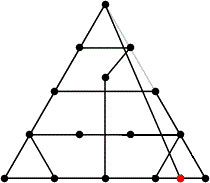
L = 6.763+
(Maurizio Morandi)
|
17
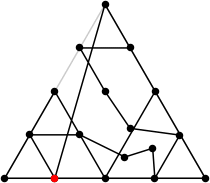
L = 6.917+
(Rob Pratt)
| 18
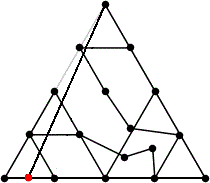
L = 7.084+
(Maurizio Morandi)
| 19
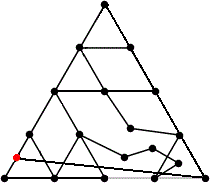
L = 7.225+
(Maurizio Morandi)
| 20
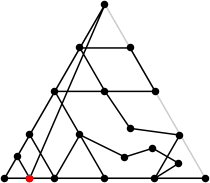
L = 7.350+
(Rob Pratt)
| 21
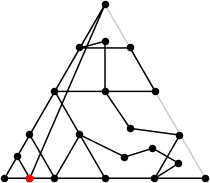
L = 7.480+
(Rob Pratt)
| |
Longest Known Greedy Cycles for Circles
2
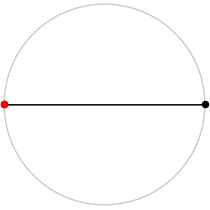
L = 2
| 3
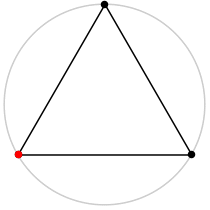
L = 3√3/2 = 2.598+
| 4
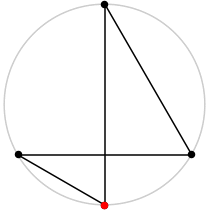
L = 3/2 + √3 = 3.232+
| 5
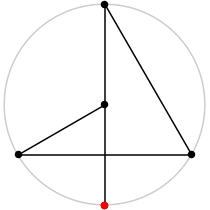
L = 2 + √3 = 3.732+
| 6
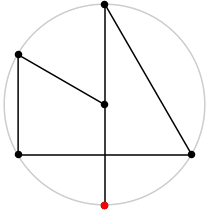
L = 5/2 + √3 = 4.232+
|
7
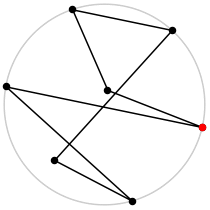
L = 4.614+
(Rob Pratt)
| 8
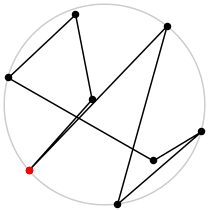
L = 4.948+
(Rob Pratt)
| 9
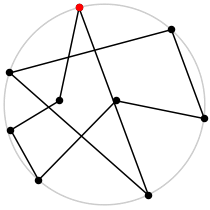
L = 5.265+
(Rob Pratt)
| 10
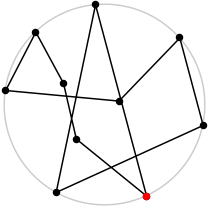
L = 5.554+
(Rob Pratt)
| 11
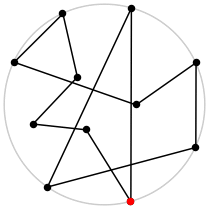
L = 5.824+
(Rob Pratt)
|
12
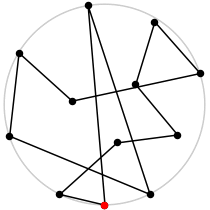
L = 6.084+
(Rob Pratt)
| 13
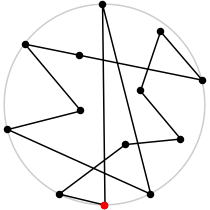
L = 6.335+
(Rob Pratt)
| 14
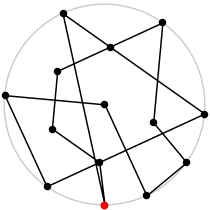
L = 6.595+
(Rob Pratt)
| 15
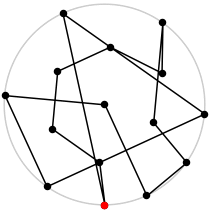
L = 6.846+
(Rob Pratt)
| 16
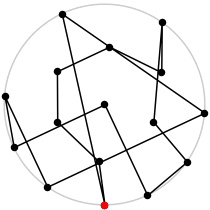
L = 7.066+
(Rob Pratt)
|
17
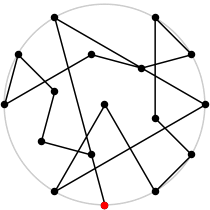
L = 7.286+
(Rob Pratt)
| 18
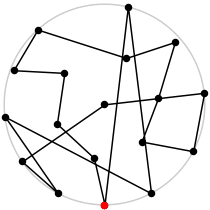
L = 7.490+
(Rob Pratt)
| 19
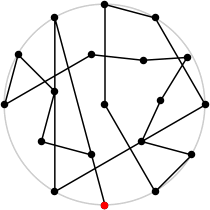
L = 7.723+
(Rob Pratt)
| 20
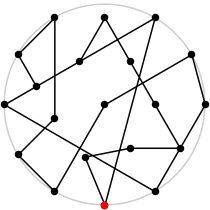
L = 7.903+
(Rob Pratt)
| 21
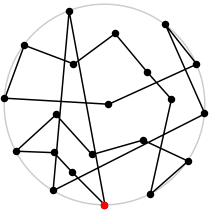
L = 8.037+
(Rob Pratt)
| |
Bill Cook pointed out that the greedy cycle is no more than (1 + ln n)/2 times the optimal length, and that ln n is the right order of magnitude of that ratio, as indicated on page 8 of this paper.
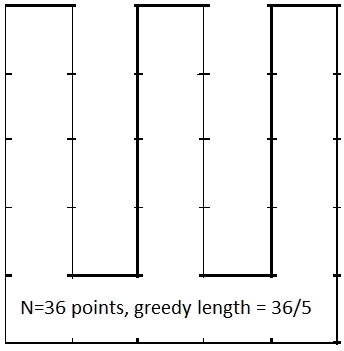
For greedy cycles inside squares, Mike Elgersma conjectured that 2√(n–1) ≤ L(n) ≤ 3√(n–1). He showed that L(4n2) ≥ 4n2/(2n–1) for the unit square below. A better bound can be found in equation (20) of this paper. More about the d-dimensional problem can be found here.
If you can extend any of these results, please
e-mail me.
Click here to go back to Math Magic. Last updated 5/10/15.




























































