Problem of the Month (May 2020)

Given two relatively prime positive integers m and n, can you find a rectangle that can be tiled with tiles that are a disjoint connected union of a square of side m and a square of side n? If so, what is the smallest one? If these are rare, then what about the union of 3 different sized squares?

ANSWERS

Solutions were sent by George Sicherman, Patrick Hamlyn, and Torsten Ueckerdt.

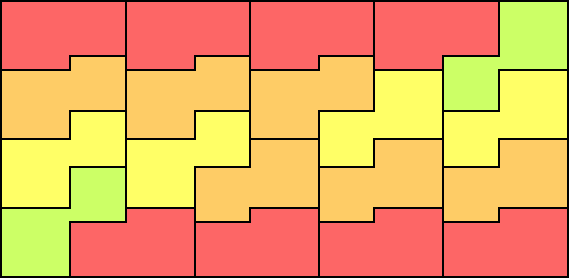
For two squares, there are solutions for m=n–1 by alternating columns of squares of different sizes, like this one.

4, 5

There are also these solutions with m=n–2.

1, 3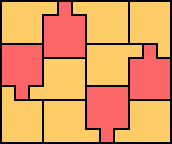
3, 5 (PH)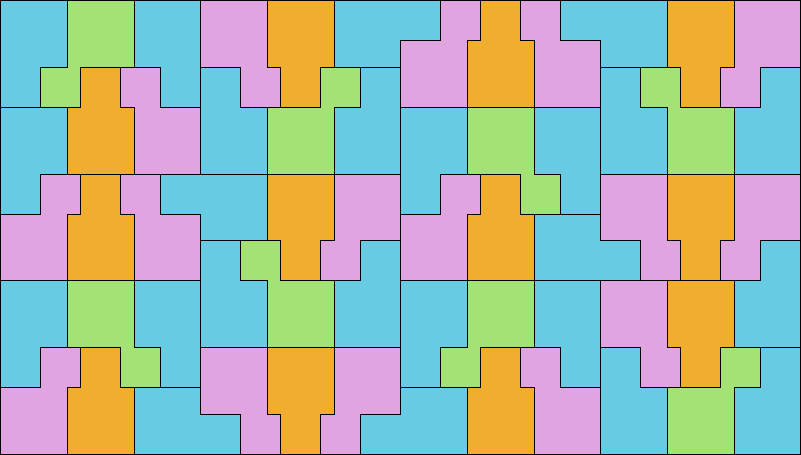

Then Torsten Ueckerdt found a similar infinite family for m=n–2, explained by this picture:

Torsten Ueckerdt also proved that there are no other solutions for m<n/2. This means the smallest open case is n=7 and m=4.

For three squares, there are more solutions:

1, 2, 3 (GS)
1, 2, 4 (GS)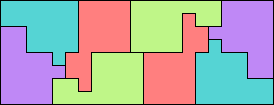
1, 3, 4 (GS)
2, 3, 4 (GS)
1, 2, 5 (GS)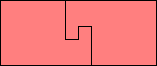
1, 3, 5 (GS)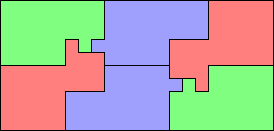

1, 4, 5 (GS)
2, 3, 5
? 2, 4, 5 (GS)
3, 4, 5 (PH)
1, 2, 6
? 1, 3, 6
? 1, 4, 6
? 1, 5, 6
?

2, 3, 6 (PH)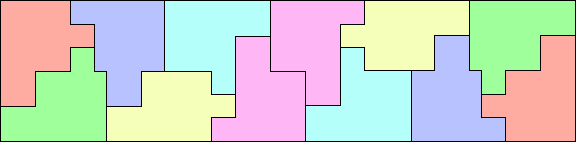
2, 5, 6 (GS)
3, 4, 6 (PH)

3, 5, 6 (GS)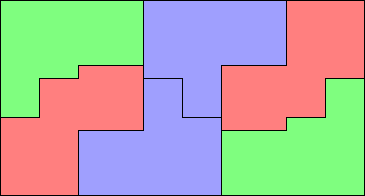
4, 5, 6
? 2, 5, 7 (PH)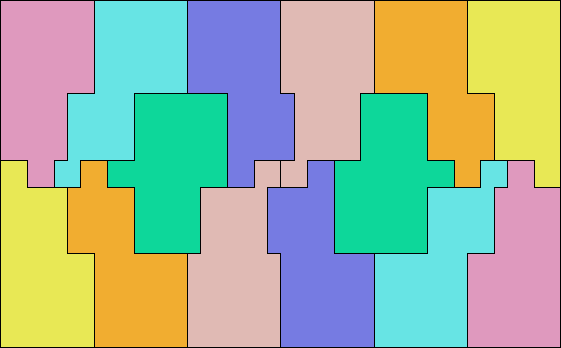
6, 9, 13 (PH)

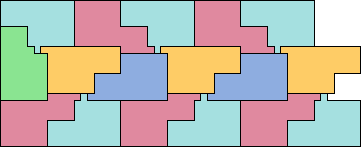
Patrick Hamlyn found that squares of sizes 1, 4, and 7 can tile a half strip:

1, 4, 7 (PH)

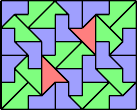
George Sicherman also extended the problem to tans:

1, 2 (GS)

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 5/29/20.