Problem of the Month (May 1999)

The surround number of a polyomino is the number of different ways that the polyomino can be surrounded by non-overlapping copies of the same shape. A polyomino is considered surrounded if every unit edge is shared completely by a neighboring polyomino. Reflections of polyominoes are not allowed.

For example, the surround number of a cross is 2, the tiling below and its mirror image:

Which positive integers are the surround numbers of some shape? In particular, is 3 a surround number? What are the surround numbers of the small polyominoes? What is the surround number of an m×n rectangle? For what other families of polyominoes can we compute surround numbers?

ANSWERS

Brendan Owen, Andrew Bayly, and Joe DeVincentis proved that every positive integer is the surround number of some polyomino.

Owen found a general formula for the surround number of an m×n rectangle. It's pretty complicated. An n×n square has surround number 2n²–1. For n ≥ 2, an n×1 rectangle has surround number (n⁴+22n³+105n²–56n–8) / 4. For n ≥ 3, an n×2 rectangle has surround number (n⁴+32n³+344n²+768n+400) / 16 if n is even and (n⁴+32n³+278n²+656n+361) / 16 if n is odd.

Here are some polyominoes with surround number 3, and the people who found them:

Polyominoes with Surround Number 3

Polyomino	Author
	Erich Friedman
	Brendan Owen
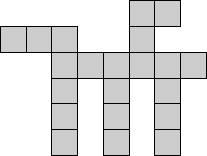	Andrew Bayly
	Joe DeVincentis

Here are the surround numbers of some small polyominoes:

Small Polyominoes

Polyomino	Surround Number
	1
	123
	7555
	361
	7
	161
	13355
	2794
	778

Here are the smallest polyominoes with a given surround number. These are all due to Brendan Owen.

Smallest Polyominoes with Small Surround Numbers

Surround Number	Polyomino	Area
0		7
1		1
2		5
3		9
4		8
5		9
6		9
7		4
8		8
9		7
10		9

Surround Number	Polyomino	Area
11		9
12		9
13		9
14		8
15		9
16		6
17		9
18		8
19		8
20		9

This sequence of values of the smallest area polyomino to have surround number n: 7, 1, 5, 9, 8, 9, 9, 4, 8, 7, 9, 9, 9, 9, 8, 9, 6, 9, 8, 8, 9, 8, 8, 7, 9, 8, 7, 8, 8, 9, 8, 8, 9, 9, 8, 9, 9, 9, 9, 8, 9, 6, 8, 9, 10, 9, 9, 8, 6, 7, 8, 8, 8, 9, 8, 9, 9, 9, 10, 9, 9, 8, 9, 9, 9, 9, 9, 9, 9, 8, 9, 9, 7, 8, 8, 9, 9, 7, 8, 7, 9, 9, 9, 9, 9, 9, 8, 9, 9, 9, 9, 9, 9, 9, 8, 9, 9, 8, 9, 9, 9, . . . is now sequence A047875 of the Encyclopedia of Integer Sequences.

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 3/5/02.