Problem of the Month (June 2002)

This month we consider tilings of squares with consecutive squares. It is well known that the only non-trivial solution of 1² + 2² + ^{. . .} + n² = k² is n=24 and k=70. Unfortunately, it has been proved that a square of size 70 cannot be tiled with squares of sizes 1 through 24. (There is a packing without the square of size 7. Can you find it?)

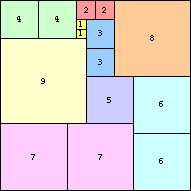
It turns out there ARE tilings of squares by consecutive squares if we allow either 1 or 2 squares of each size. We such a tiling a diverse tiling. The smallest non-trivial diverse tiling of a square is the 20×20 square below:

What other diverse tilings of a square can you find? Are there many diverse tilings of rectangles? What's the largest one you can find?

I'll pay $10 for the first diverse square tiling where repeated squares don't touch. I'll also pay $10 for the first diverse square tiling that contains 1 square each of odd sizes and 2 squares each of even sizes. I'll also pay $10 for the first diverse tiling of a triangle by smaller equilateral triangles.

ANSWERS

Antonio Ianiero found diverse square tilings of sizes 1-10 in a 25×25 square, sizes 1-12 in a 30×30 square, and sizes 1-12 in a 33×33 square.

Patrick Hamlyn wrote a computer program to search for diverse square tilings. He found that all diverse square tilings smaller than 48×48 have two equal squares that touch. His results are below:

Number of Diverse Square Tilings

k	Number of Diverse Tilings of k×k Square	Author
1	1	Trivial
20	1	Patrick Hamlyn
23	1	Patrick Hamlyn
25	1	Patrick Hamlyn
26	1	Patrick Hamlyn
29	93	George Sicherman
30	6	George Sicherman
31	205	George Sicherman
32	439	George Sicherman
33	412	George Sicherman
34	83	George Sicherman
35	240	George Sicherman
36	136	Patrick Hamlyn
37	359	George Sicherman
38	64	George Sicherman
39	64	George Sicherman
40	54	George Sicherman

Here are some pictures of small diverse square tilings:

Diverse Square Tilings

n	k
1	1
9	20, 23
10	25, 26
11	29
12	29, 30, 31, 32, 33
13	32, 33, 34, 35, 36, 37
14	35, 36, 37, 38, 40

And here are some pictures of small non-square diverse rectangle tilings:

Diverse Rectangle Tilings

n	Rectangles
1	2×1
2	3×2, 5×2
3	5×3, 8×3
4	8×7
5	9×8
7	15×13
8	17×15, 18×15, 28×14
9	20×17, 21×15, 24×14, 24×18, 25×21, 26×15, 28×17, 30×14
10	26×22, 26×24, 27×20, 27×23, 28×17, 28×22, 28×26, 30×15, 30×20, 30×24,32×16, 36×15, 36×19, 42×14
11	29×21, 30×25, 30×26, 30×29, 31×27, 31×29, 31×30, 35×25, 37×20, 37×22, 37×26, 39×19, 39×22, 40×20

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 2/12/13.