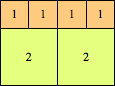
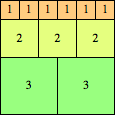
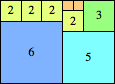
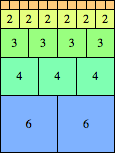
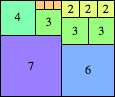
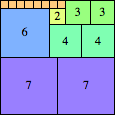
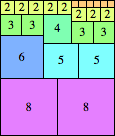
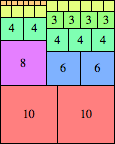
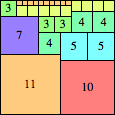
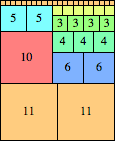
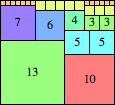
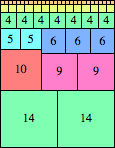
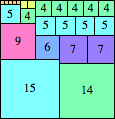
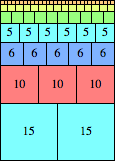
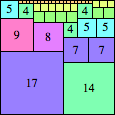
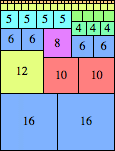
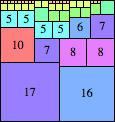
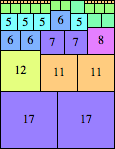
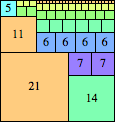
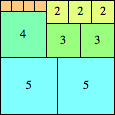
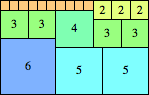
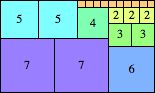
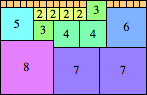
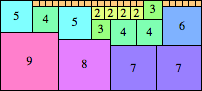
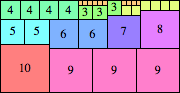
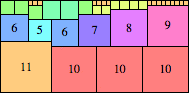
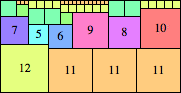
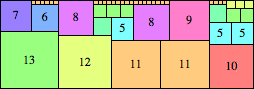
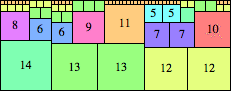
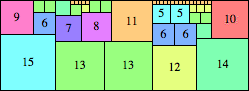
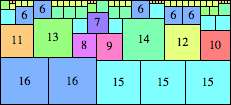
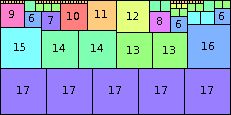
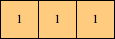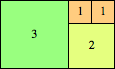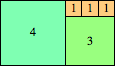We can ask the same question about cubes. What are the highest Hanoi boxes? For which n≤100 is the highest box higher than just the sum of the proper factors of n?
n=37
height = 40
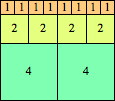
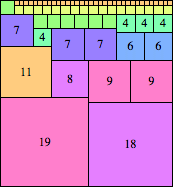
| n=38
height = 50
(Maurizio Morandi)
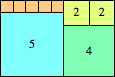
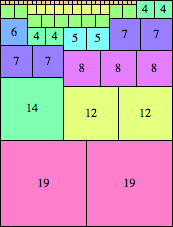
| n=39
height = 42
(Maurizio Morandi)
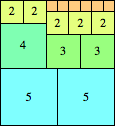
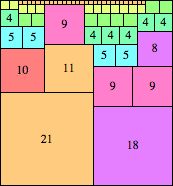
| n=40
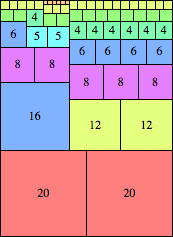
height = 55
| n=41
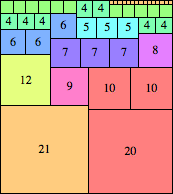
height = 46
(Maurizio Morandi)
|
n=42
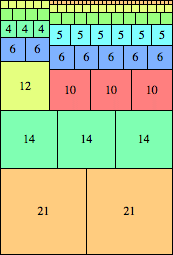
height = 62
(Maurizio Morandi)
| n=43
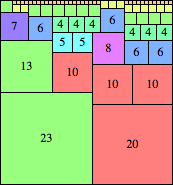
height = 46
| n=44
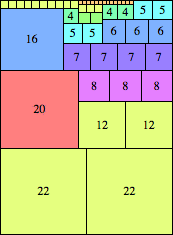
height = 60
(Maurizio Morandi)
| n=45
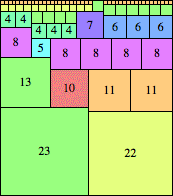
height = 51
| n=46
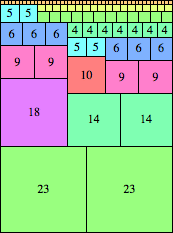
height = 62
|
n=47
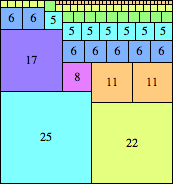
height = 50
(Maurizio Morandi)
| n=48
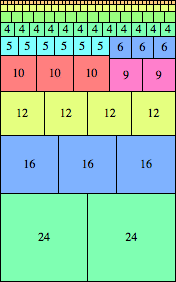
height = 77
| n=49
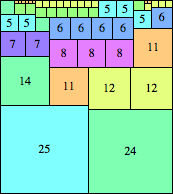
height = 55
(Maurizio Morandi)
| n=50
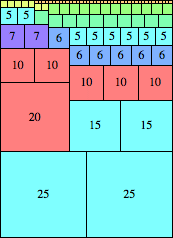
height = 69
(Maurizio Morandi)
| n=51
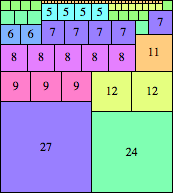
height = 57
(Maurizio Morandi)
|
n=52
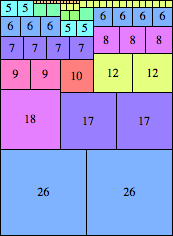
height = 71
(Maurizio Morandi)
| n=53
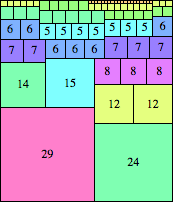
height = 62
(Maurizio Morandi)
| n=54
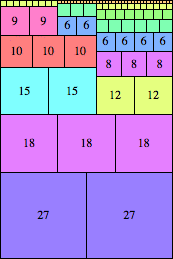
height = 81
| n=55
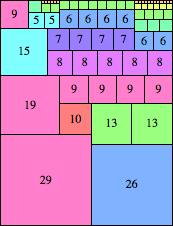
height = 72
(Maurizio Morandi)
| n=56
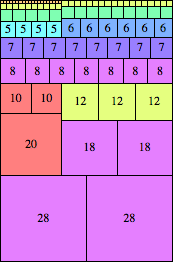
height = 85
(Maurizio Morandi)
|
n=57
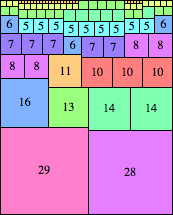
height = 71
(Maurizio Morandi)
| n=58
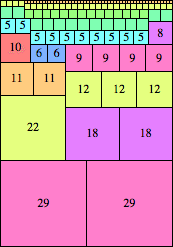
height = 83
(Maurizio Morandi)
| n=59
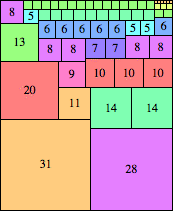
height = 72
(Maurizio Morandi)
| n=60
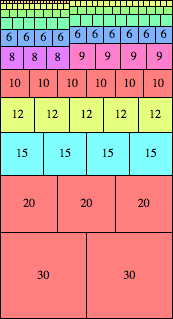
height = 111
(Maurizio Morandi)
| n=61
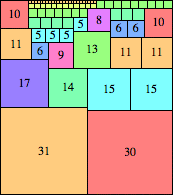
height = 69
(Bryce Herdt)
|
n=62
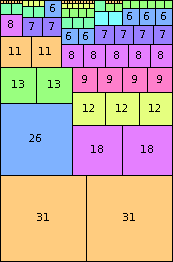
height = 94
(Joe DeVincentis)
| n=63
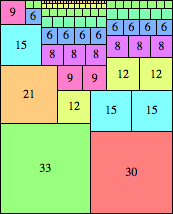
height = 78
(Maurizio Morandi)
| n=64
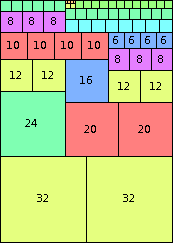
height = 90
(Joe DeVincentis)
| n=65
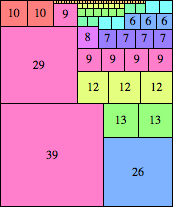
height = 78
(Maurizio Morandi)
| n=66
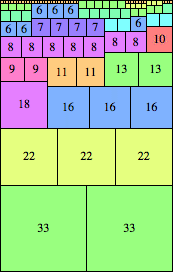
height = 104
(Maurizio Morandi)
|
n=67
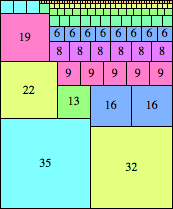
height = 81
(Maurizio Morandi)
| n=68
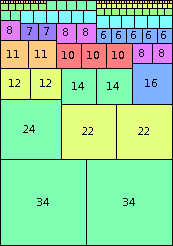
height = 97
(Joe DeVincentis)
| n=69
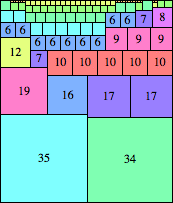
height = 81
(Maurizio Morandi)
| n=70
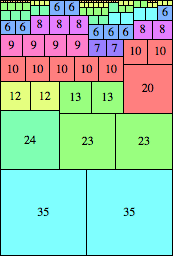
height = 104
(Maurizio Morandi)
| n=71
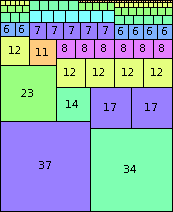
height = 87
(Joe DeVincentis)
|
n=72
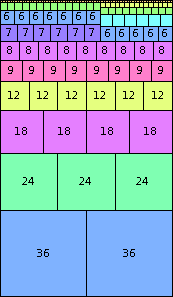
height = 124
(Joe DeVincentis)
| n=73
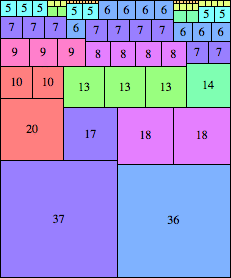
height = 88
(Maurizio Morandi)
| n=74
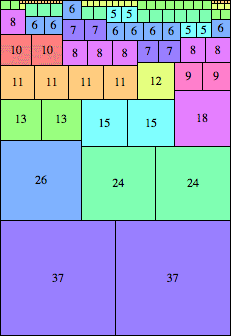
height = 108
(Maurizio Morandi)
| n=75
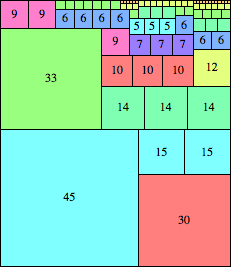
height = 87
(Maurizio Morandi)
|
n=76
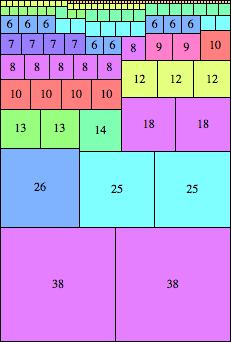
height = 113
(Maurizio Morandi)
| n=77
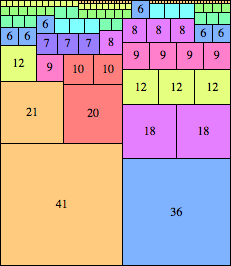
height = 89
(Maurizio Morandi)
| n=78
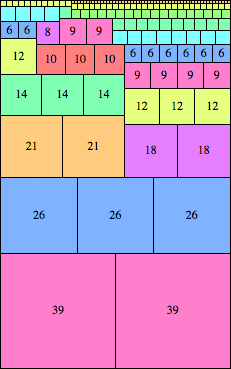
height = 125
(Maurizio Morandi)
| n=79
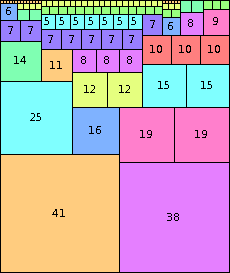
height = 94
(Joe DeVincentis)
|
n=80
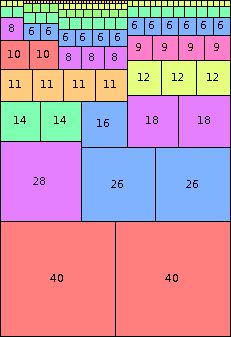
height = 117
(Joe DeVincentis)
| n=81
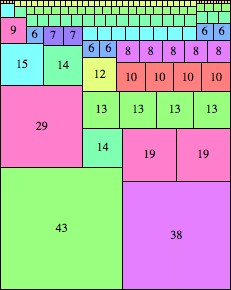
height = 102
(Maurizio Morandi)
| n=82
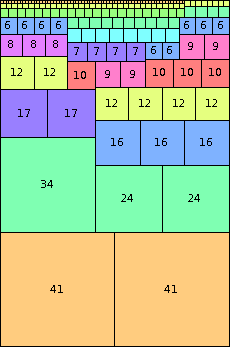
height = 124
(Joe DeVincentis)
| n=83
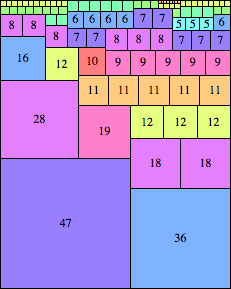
height = 104
(Maurizio Morandi)
|
n=84
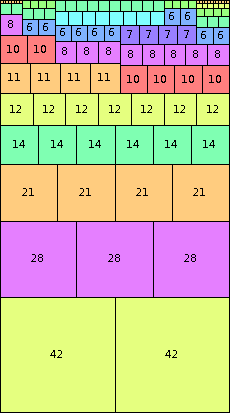
height = 151
(Joe DeVincentis)
| n=85
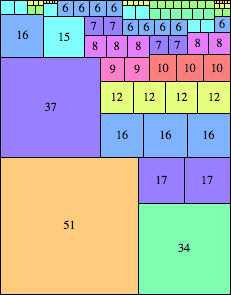
height = 109
(Maurizio Morandi)
| n=86
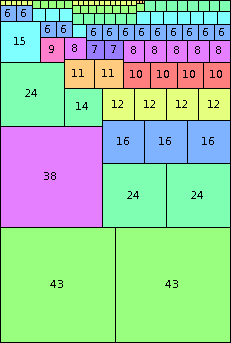
height = 128
(Joe DeVincentis)
| n=87
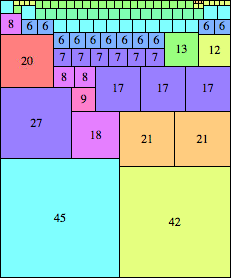
height = 105
(Maurizio Morandi)
|
n=88
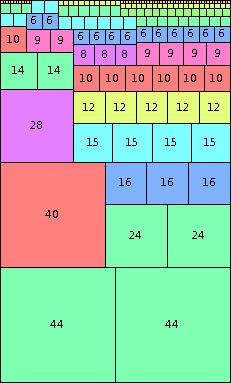
height = 146
(Joe DeVincentis)
| n=89
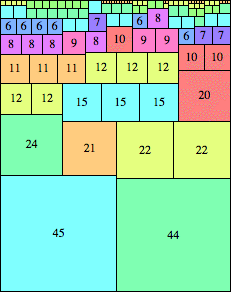
height = 113
(Maurizio Morandi)
| n=90
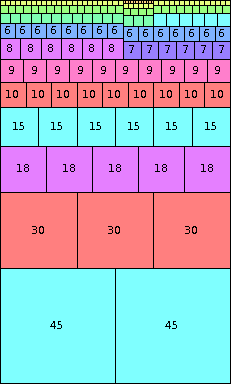
height = 150
(Joe DeVincentis)
| n=91
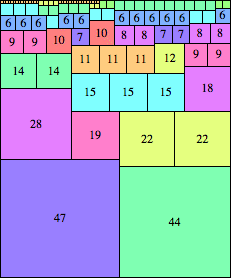
height = 110
(Maurizio Morandi)
|
n=92
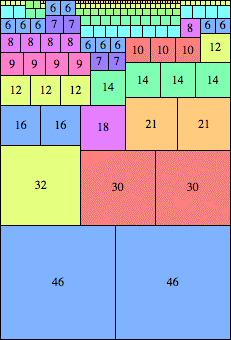
height = 136
(Maurizio Morandi)
| n=93
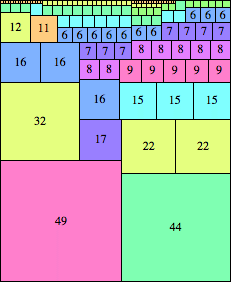
height = 114
(Maurizio Morandi)
| n=94
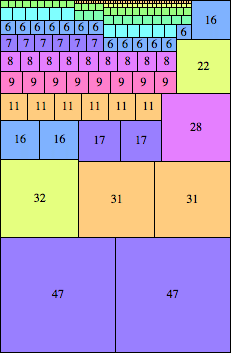
height = 144
(Maurizio Morandi)
| n=95
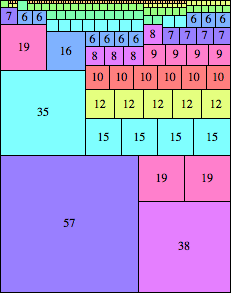
height = 121
(Maurizio Morandi)
|
n=96
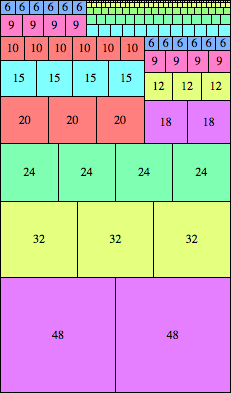
height = 164
(Maurizio Morandi)
| n=97
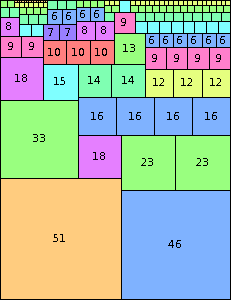
height = 126
(Joe DeVincentis)
| n=98
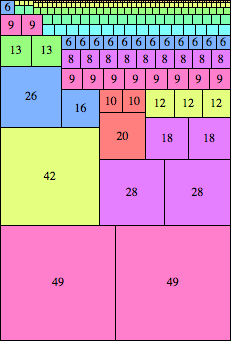
height = 145
(Maurizio Morandi)
| n=99
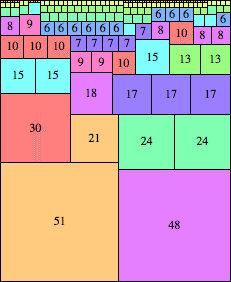
height = 121
(Maurizio Morandi)
|
n=100
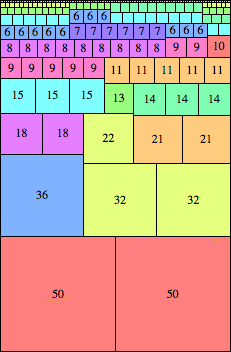
height = 153
(Maurizio Morandi)
|
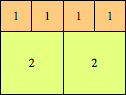
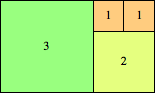
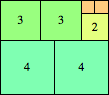
What are the thinnest Hanoi towers that contain all the squares of sides 1 through n? Here are the best-known results:
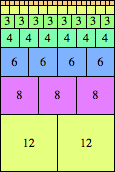
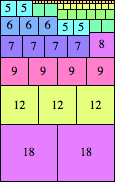
Here are the important layers for the tallest known Hanoi boxes that are taller than the sum of the proper divisors of n:
n=22
height = 18
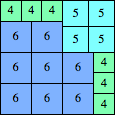
11+6+1
11+5+2
11+4+2+1
| n=26
height = 20
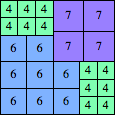
13+7
13+6+1
13+4+2+1
| n=33
height = 20
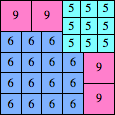
11+9
11+6+3
11+5+3+1
| n=34
height = 24
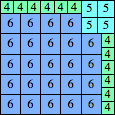
17+6+1
17+5+2
17+4+2+1
| n=38
height = 29
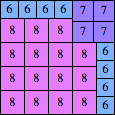
19+8+2
19+7+2+1
19+6+3+1
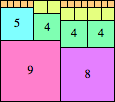
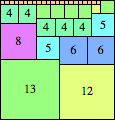
| n=39
height = 23
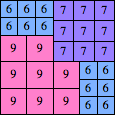
13+9+1
13+7+3
13+6+3+1
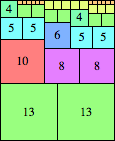
| n=43
height = 8
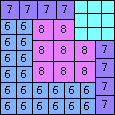
8
7+1
6+2
5+3
(Joe DeVincentis)
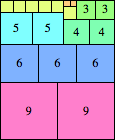
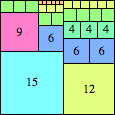
| n=44
height = 48
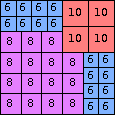
22+11+10+5
22+11+8+4+2+1
22+11+6+4+3+2
(Joe DeVincentis)
|
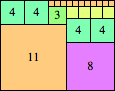
n=46
height = 35
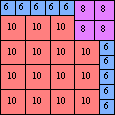
23+10+2
23+8+4
23+6+3+2+1
(Joe DeVincentis)
| n=50
height = 45
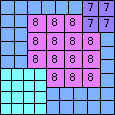
25+10+8+2
25+10+7+2+1
25+10+6+3+1
25+10+5+4+1
(Joe DeVincentis)
| n=51
height = 29
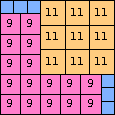
17+11+1
17+9+3
17+6+3+2+1
(Joe DeVincentis)
| n=52
height = 54
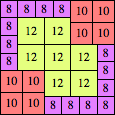
26+13+12+3
26+13+10+5
26+13+8+4+2+1
(Maurizio Morandi)
| n=57
height = 31
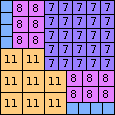
19+11+1
19+7+5
19+8+4
19+6+3+2+1
(Joe DeVincentis)
| n=58
height = 44
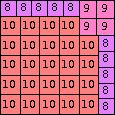
29+10+5
29+9+6
29+8+4+2+1
(Joe DeVincentis)
| n=59
height = 8
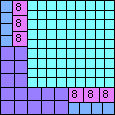
8
7+1
5+3
(Joe DeVincentis)
|
n=62
height = 46
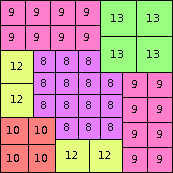
31+13+2
31+12+3
31+10+5
31+9+6
31+8+4+2+1
(Joe DeVincentis)
| n=64
height = 64
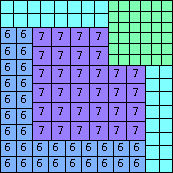
32+16+8+7+1
32+16+8+6+2
32+16+8+5+2+1
32+16+8+4+3+1
(Joe DeVincentis)
| n=65
height = 24
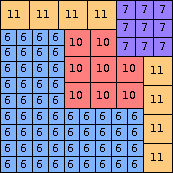
13+11
13+10+1
13+7+3+1
13+6+3+2
(Joe DeVincentis)
| n=66
height = 83
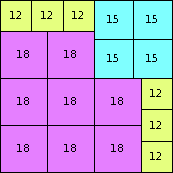
33+22+18+9+1
33+22+15+10+3
33+22+12+6+4+3+2+1
(Joe DeVincentis)
| n=68
height = 69
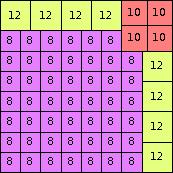
34+17+12+4+2
34+17+12+3+2+1
34+17+10+5+2+1
34+17+8+4+3+2+1
(top view below)
(Bryce Herdt)
| n=69
height = 38
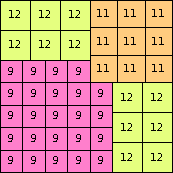
23+12+3
23+12+2+1
23+11+3+1
23+9+3+2+1
(top view below)
(Bryce Herdt)
|
n=71
height = 13
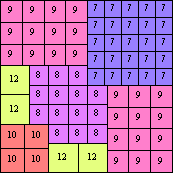
12+1
10+2
9+3+1
8+4+1
7+5+1
(Joe DeVincentis)
| n=73
height = 12
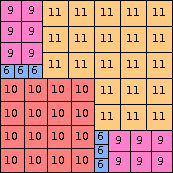
11+1
10+2
9+3
6+3+2+1
(Joe DeVincentis)
| n=74
height = 52
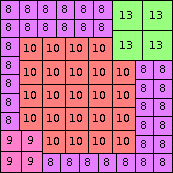
37+13+2
37+10+5
37+9+6
37+8+4+2+1
(Joe DeVincentis)
| n=75
height = 53
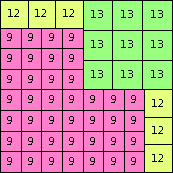
25+15+13
25+15+12+1
25+15+9+3+1
(Joe DeVincentis)
| n=76
height = 85
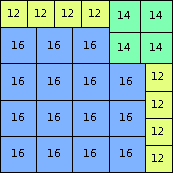
38+19+16+8+4
38+19+14+7+4+2+1
38+19+12+6+4+3+2+1
(Joe DeVincentis)
| n=78
height = 99
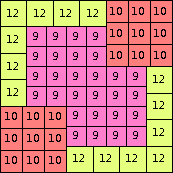
39+26+13+12+6+3
39+26+13+10+6+5
39+26+13+9+6+3+2+1
(Joe DeVincentis)
|
n=79
height = 13
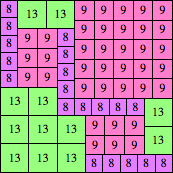
13
9+3+1
8+4+1
(Maurizio Morandi)
| n=81
height = 44
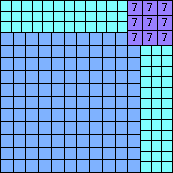
27+9+7+1
27+9+6+2
27+9+5+3
(Joe DeVincentis)
| n=82
height = 65
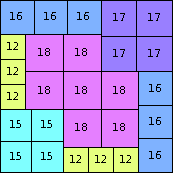
41+18+6
41+(24)
41+16+8
41+15+6+3
41+12+6+4+2
(Joe DeVincentis)
| n=83
height = 8
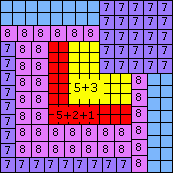
8
7+1
6+2
5+3
5+2+1
(Joe DeVincentis)
| n=85
height = 33
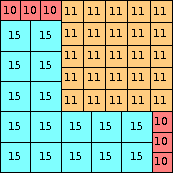
17+15+1
17+11+5
17+10+5+1
(Joe DeVincentis)
| n=86
height = 60
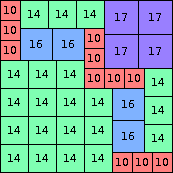
43+17
43+16+1
43+14+2+1
43+10+5+2
(Joe DeVincentis)
|
n=87
height = 41
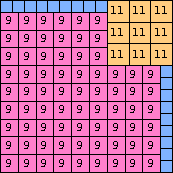
29+11+1
29+9+3
29+6+3+2+1
(Joe DeVincentis)
| n=88
height = 97
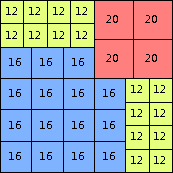
44+22+20+10+1
44+22+16+8+4+2+1
44+22+12+8+6+4+1
(Joe DeVincentis)
| n=89
height = 12

12
11+1
9+3
8+4
(Joe DeVincentis)
| n=91
height = 25
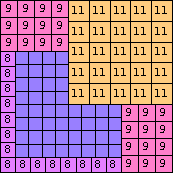
13+11+1
13+9+3
13+8+4
13+7+4+1
(Joe DeVincentis)
| n=92
height = 97
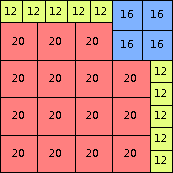
46+23+20+5+2+1
46+23+16+8+4
46+23+12+6+4+3+2+1
(Joe DeVincentis)
| n=93
height = 46
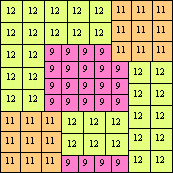
31+12+3
31+12+2+1
31+9+3+2+1
31+11+3+1
(top view below)
(Joe DeVincentis)
|
n=94
height = 71
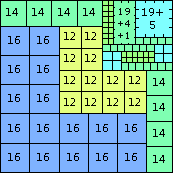
47+19+5
47+19+4+1
47+19+3+2
47+16+8
47+14+7+2+1
47+12+6+4+2
(Joe DeVincentis)
| n=95
height = 31
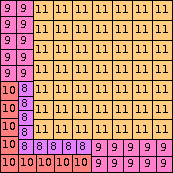
19+11+1
19+10+2
19+9+3
19+8+4
(Joe DeVincentis)
| n=97
height = 14
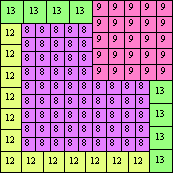
13+1
12+2
9+5
8+4+2
(Joe DeVincentis)
| n=98
height = 78

49+14+10+5
49+14+9+6
49+14+8+4+2+1
(Joe DeVincentis)
| n=100
height = 119
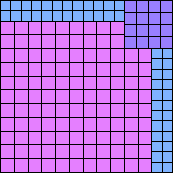
50+25+20+10+8+4+2
50+25+20+10+7+4+2+1
50+25+20+10+6+4+3+1
(Joe DeVincentis)
|