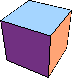
1
(Joe DeVincentis)

8
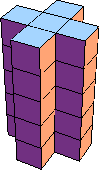
25
(George Sicherman)
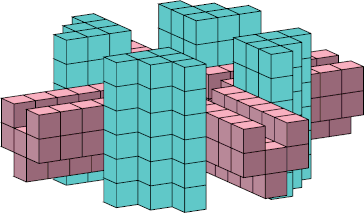
288
(George Sicherman)
A polycube is a solid made from gluing unit cubes together along their faces. If S is a set of positive integers, we call a polycube P a S-faced polycube if S is the set of areas of the faces of P. What is the smallest (in terms of volume) S-faced polycube for various S?
When S={n}, solutions are known for for all n except n = 2 and n = 3. Can you find a solution for one of these values of n? Can you prove they don't exist? Can you find smaller solutions for the other values of n?
Solutions are known for all S={m,n}. Can you improve any of the best known solutions? Is every S={m,n,p} possible?
Given two particular polyominoes, is there a polycube that only has those two faces?
If there are an equal number n of faces with each area in S, we call P a balanced S-faced polycube. What balanced polycubes exist? In particular, what is the smallest k or the smallest n for which a {1,2,3,...k}n balanced polycube exists?
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
 1 | none (Joe DeVincentis) | ? |  8 |  25 (George Sicherman) |  288 (George Sicherman) |
| 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|
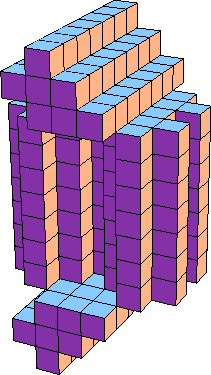 245 (Bryce Herdt) | 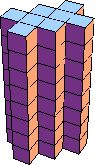 64 |  27 |  500 (Bryce Herdt) |  121 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|
 144 |  169 |  196 | 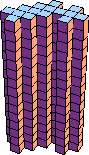 225 |  64 | 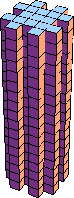 289 |  324 | 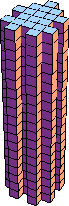 361 |  200 |
| m \ n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 2 |  2 | ||||||||
| 3 |  3 | 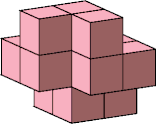 13 (George Sicherman) | |||||||
| 4 |  4 | 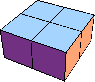 4 | 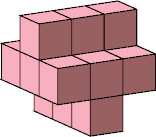 15 (George Sicherman) | ||||||
| 5 | 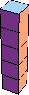 5 | 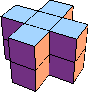 10 |  12 |  20 | |||||
| 6 |  6 |  12 |  9 | 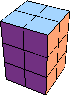 12 |  30 | ||||
| 7 |  7 | 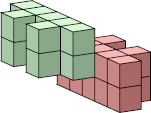 28 (George Sicherman) | 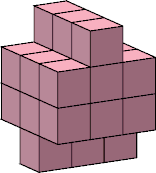 24 (George Sicherman) |  36 (Bryce Herdt) | 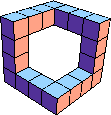 18 |  72 (George Sicherman) | |||
| 8 |  8 | 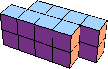 16 | 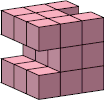 21 (George Sicherman) |  16 |  40 |  48 | 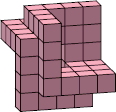 48 (George Sicherman) | ||
| 9 | 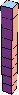 9 |  18 |  9 |  32 (Bryce Herdt) |  45 |  18 |  24 |  53 (George Sicherman) | |
| 10 | 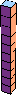 10 |  20 | 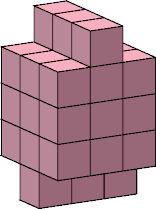 33 (George Sicherman) |  20 | 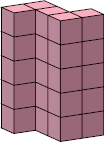 25 (George Sicherman) | 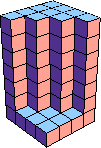 40 (Bryce Herdt) | 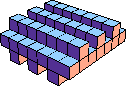 91 |  80 |  90 |
We can also ask for solutions that have the same number of faces with area m and n.
| m \ n | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 2 |  10 (George Sicherman) | ||||
| 3 | 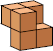 6 (George Sicherman) |  18 (George Sicherman) | |||
| 4 | 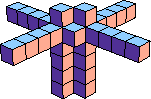 30 (Bryce Herdt) | 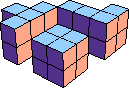 24 (Bryce Herdt) |  15 (George Sicherman) | ||
| 5 | 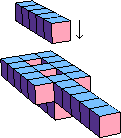 28 (Bryce Herdt) | 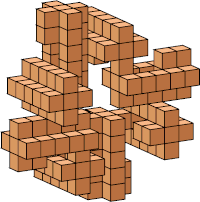 164 (George Sicherman) |  12 | 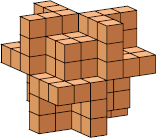 108 (George Sicherman) | |
| 6 | 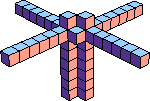 42 (Bryce Herdt) |  12 (George Sicherman) |  18 (George Sicherman) |  24 | 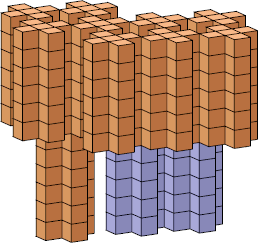 365 (George Sicherman) |
| 7 | 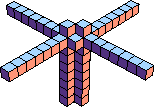 48 (Bryce Herdt) |  469 (George Sicherman) |  126 (Bryce Herdt) |  253 (George Sicherman) | 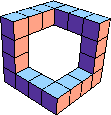 18 |
| 8 |  25 (Bryce Herdt) | 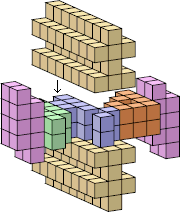 208 (Bryce Herdt) | 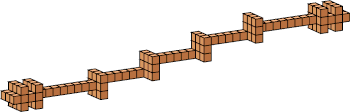 115 (Bryce Herdt) |  32 (Bryce Herdt) | 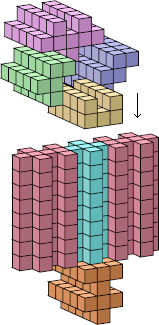 323 (George Sicherman) |
| 9 | 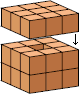 26 (Bryce Herdt) | 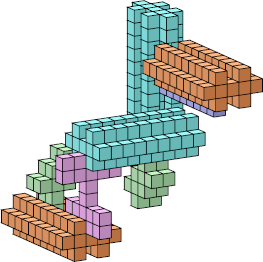 379 (George Sicherman) |  90 (Bryce Herdt) |  131 (George Sicherman) |  46 |
| 10 | 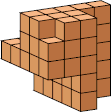 62 (George Sicherman) | 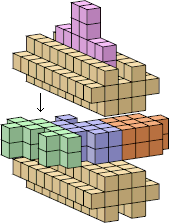 276 (George Sicherman) | 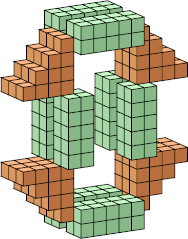 280 (Bryce Herdt) | 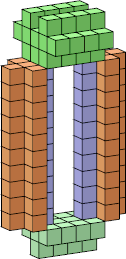 156 (George Sicherman) |  50 (George Sicherman) |
| m \ n | 6 | 7 | 8 | 9 |
|---|---|---|---|---|
| 7 |  319 (George Sicherman) | |||
| 8 |  436 (George Sicherman) | 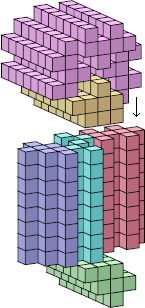 412 (Bryce Herdt) | ||
| 9 |  198 (Bryce Herdt) |  24 |  53 (George Sicherman) | |
| 10 | 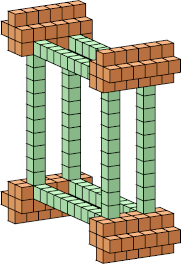 224 (George Sicherman) | 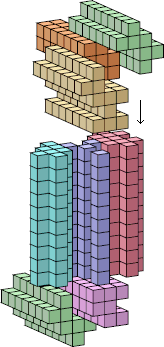 476 (George Sicherman) | 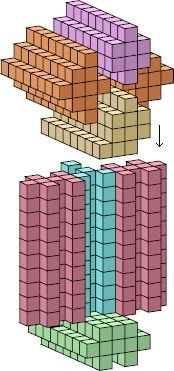 584 (Bryce Herdt) |  684 (Bryce Herdt) |
| m \ n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
| 3 |  3 (GS) | |||||||
| 4 |  4 (GS) |  4 (GS) | ||||||
| 5 |  5 (GS) | 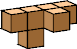 6 (GS) |  8 (GS) | |||||
| 6 |  6 (GS) |  6 (GS) |  7 (GS) | 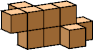 10 (GS) | ||||
| 7 |  7 (GS) |  7 (GS) | 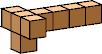 8 (GS) |  7 (GS) | 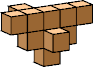 11 (GS) | |||
| 8 | 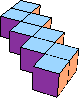 8 | 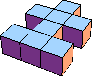 8 | 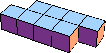 8 |  9 (GS) |  9 |  11 (GS) | ||
| 9 | 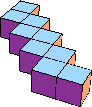 9 | 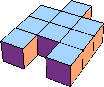 9 | 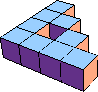 9 | 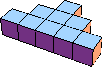 9 | 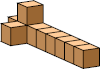 10 (GS) | 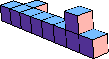 10 | 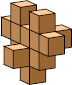 13 (GS) | |
| 10 |  10 (GS) |  10 (GS) |  10 (GS) |  10 (GS) | 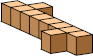 10 (GS) |  10 (GS) | 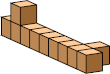 11 (GS) | 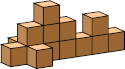 14 (GS) |
| m \ n | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|
| 4 |  6 (GS) | ||||||
| 5 |  8 (GS) |  10 (GS) | |||||
| 6 |  6 (GS) |  8 (GS) | 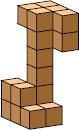 18 (GS) | ||||
| 7 |  13 (GS) |  14 (GS) |  12 (GS) |  14 (GS) | |||
| 8 |  16 (GS) | 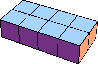 8 | 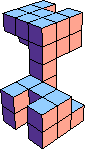 29 (BH) |  16 | 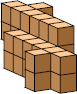 28 (GS) | ||
| 9 | 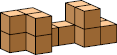 14 (GS) |  18 (BH) | 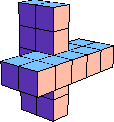 19 (BH) | 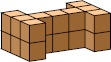 18 (GS) |  16 (GS) |  18 (BH) | |
| 10 |  16 (GS) | 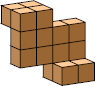 16 (GS) |  10 (GS) | 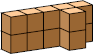 12 (GS) |  14 (GS) |  20 (GS) | 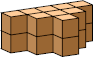 18 (GS) |
| m \ n | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|
| 5 | 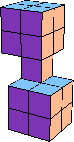 17 (BH) | |||||
| 6 | 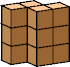 12 (GS) |  15 (GS) | ||||
| 7 | 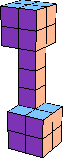 19 (BH) |  14 (GS) |  21 | |||
| 8 |  12 (GS) | 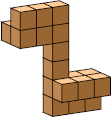 20 (GS) |  24 | 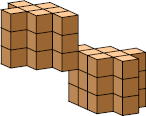 42 (GS) | ||
| 9 |  12 (GS) |  18 (BH) | 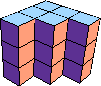 18 | 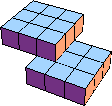 18 (BH) |  18 (BH) | |
| 10 | 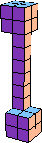 22 (BH) |  15 (BH) |  30 (GS) | 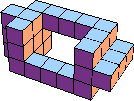 30 (BH) | 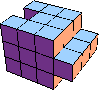 27 (BH) | 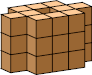 30 (GS) |
| m \ n | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|
| 6 | 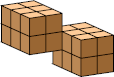 24 (GS) | ||||
| 7 | 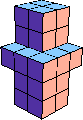 25 (BH) | 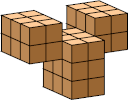 42 (GS) | |||
| 8 |  20 |  24 |  28 | ||
| 9 | 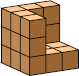 19 (GS) | 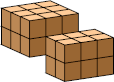 30 (GS) | 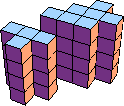 44 (BH) |  32 (GS) | |
| 10 | 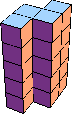 20 (BH) | 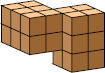 24 (GS) | 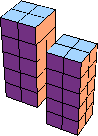 40 (BH) |  32 (GS) | 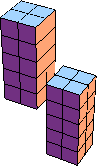 40 (BH) |
| m \ n | 6 | 7 | 8 | 9 |
|---|---|---|---|---|
| 7 | 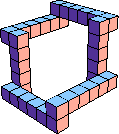 34 (BH) | |||
| 8 | 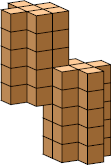 58 (GS) | 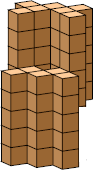 60 (BH) | ||
| 9 |  36 (GS) | 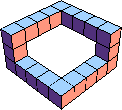 20 (BH) | 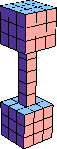 59 (BH) | |
| 10 |  30 (BH) |  35 (BH) |  40 (BH) |  45 (BH) |
| m \ n | 7 | 8 | 9 |
|---|---|---|---|
| 8 |  40 (BH) | ||
| 9 | 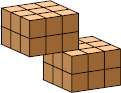 36 (GS) | 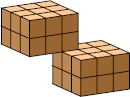 36 (GS) | |
| 10 |  54 (BH) | 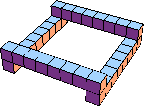 32 (BH) | 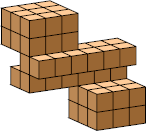 60 (GS) |
| {7,8,9} | {7,8,10} | {7,9,10} | {8,9,10} |
|---|---|---|---|
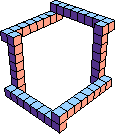 46 (BH) |  112 (GS) |  119 (BH) | 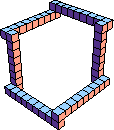 52 (BH) |
Bryce Herdt managed to prove that all triples {m,n,p} have a solution. Then, in 2021, Bryce Herdt and George Sicherman proved that any set of two or more positive integers is the set of different areas of the faces of some polycube!
 |  |  |  |  | 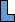 |  |  | 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|

|  2 (GS) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

| 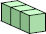 3 (GS) | ?

 4 (GS) 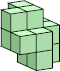 13 (GS) ?
| 
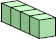 4 (GS) ?
| ?
| ?
| 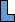
?
| 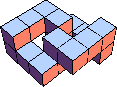 16 ?
| ?
| ?
| 
 48 (GS)  4 (GS) ?
| 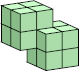 15 (GS) ?
| 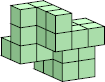 24 (GS) 
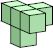 5 (GS) 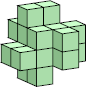 20 (GS) 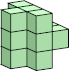 15 (GS) ?
| ?
| ?
| ?
| 
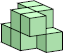 8 (GS) ?
| ?
| ?
| ?
| ?
| ?
| ?
| 
 5 (GS) ?
| ?
| ?
| ?
| ?
| ?
| ?
| ?
| 
?
| ?
| ?
| ?
| ?
| ?
| ?
| ?
| ?
| 
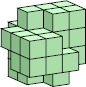 30 (GS) ?
| 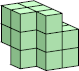 18 (GS) ?
| ?
| ?
| ?
| ?
| ?
| 
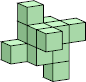 14 (GS) ?
| ?
| ?
| ?
| ?
| ?
| ?
| ?
| 
?
| ?
| ?
| ?
| ?
| ?
| ?
| ?
| ?
| 
?
| ?
| ?
| ?
| ?
| ?
| ?
| ?
| ?
| 
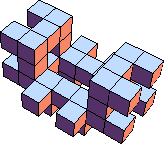 38 (BH) ?
| ?
| ?
| ?
| ?
| ?
| ?
| ?
| 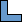
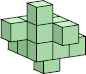 14 (GS) ?
| ?
|  12 ?
| ?
| 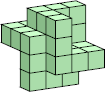 30 (GS) ?
| ?
| 
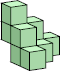 9 (GS) 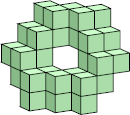 36 (GS) ?
| ?
| ?
| ?
| ?
| ?
| ?
| 
 5 (GS) 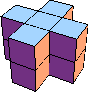 10 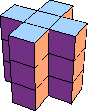 15 ?
|  20 ?
| ?
| ?
| ?
| 
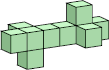 10 (GS) ?
| ?
| ?
| ?
| ?
| ?
| ?
| ?
| 
?
| ?
| ?
| ?
| ?
| ?
| ?
| ?
| ?
| |
| n=1 k=11 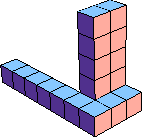 19 (AN) | n=2 k=5 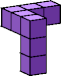 7 (GS) | n=3 k=4 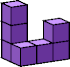 7 (GS) | n=4 k=4 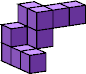 10 (GS) | n=5 k=4 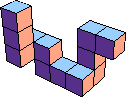 12 (AN) | n=6 k=1  1 | n=7 k=? | n=8 k=3 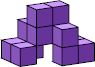 12 (GS) |
| k=1 n=6  1 | k=2 n=14 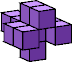 10 (GS) | k=3 n=6 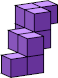 9 (GS) | k=4 n=3  7 (GS) | k=5 n=2  7 (GS) | k=6 n=2 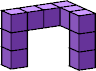 10 (GS) |
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 8/2/14.