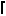Problem of the Month (June 1999)

This month, we feature several questions about palindromes, numbers which read the same forward and backward.

Question #1:

We can build palindromes out of single digits, and the arithmetic symbols: + – × ÷ ( ). The largest palindromes we can make using 1, 2, and 3 digits are: 9, 2+9=11, and 7×7×7=343. Notice that concatenation of digits is not allowed. What is the largest palindrome we can make with n digits? Why is this question not very interesting if we allow exponentiation as well?

Question #2:

The product of three or more consecutive integers can be a palindrome, like 1×2×3=6 and 77×78×79=474474. Are there any larger examples? Are there infinitely many examples?

Question #3:

Sometimes a number is a palindrome in more than one base, like 5=1012=114. For given bases a and b, what is the smallest number n > max{a,b} that is a palindrome in both base a and base b? Does there always exist such a number?

Question #4:

Some positive integers are the sum of two palindromes, and others are not. Which numbers are not? Are there only finitely many? Is every positive integer the sum of three palindromes? Is there a number n so that every positive integer is the sum of n palindromes? Which numbers are not the difference of two palindromes?

ANSWERS

Question #1:

Brendan Owen and Joseph DeVincentis found that if exponentiation is allowed, extremely large palindromes like 1+(1+9)99 could be formed.

Here are the largest palindromes that we can create using a small number of digits. There is still a lot of work to be done here.

Largest Palindromes Using a Small Number of Digits

Number of DigitsCalculation PalindromeAuthor
199Trivial
29+211Trivial
37×7×7343Proved by Erich Friedman, 1999
49 × (9×9+2)747Proved by Matt Galati, 1999
59×9×9×9–56556Proved by Erich Friedman, 2002
63×7×7×8×8×865856Proved by Erich Friedman, 2002
78×8×8×8×9 × (9+2)405504Proved by Erich Friedman, 2002
88×9×9×9×9×9×9–44251524Proved by Erich Friedman, 2002
98×8 × (5×6×8×8×8×9+2)8847488Proved by Erich Friedman, 2007
107×7×7×8 × (7×8×8×8×9–4)88499488Found by Erich Friedman, 2004
116×8×8×8×9 × (6×7×9×9×9+8)846747648Found by Erich Friedman, 2007
127×8×8×8×8×9 × (4×7×7×9×9–3)4095995904Found by Erich Friedman, 2004
139×9×9×9×9×9 × (6×7×7×7×7×9–8)68899199886Found by Marc Lapierre, 2017
14(9×9×9×9×9×5+4) × (8×8×8×8×9×9–5)97955055979Found by Marc Lapierre, 2017
157×8 × (5×9×9×9×9×9–7) × (8×9×9×9×9–7)867685586768Found by Marc Lapierre, 2017
169×8×8×8×8×8×8×7×4 × (7×7×7×7×7×8–5)8881871781888Found by Marc Lapierre, 2017
178×8×8×8×8×9 × (9×9×7+2) × (9×9×9×9×8×7+6)61655222255616Found by Marc Lapierre, 2017
189×8×8 × (8×8×8×8×8×7+1) × (9×9×9×9×9×9×9–1)631931242139136Found by Marc Lapierre, 2017
199×8×8 × (6×8×8×8×8×8×8×9×9+5) × (7×8×8×8×9+7)2367573333757632Found by Marc Lapierre, 2017
209×9×7 × (8×8×8×8×8×9×9×9×9+3) × (6×9×9×9×9×9+8)43189347374398134Found by Marc Lapierre, 2017
217×9 × (8×8×8×8×8×9×9×9+5) × (2×8×8×9×9×9×9×9×9+3)86925062526052968Found by Marc Lapierre, 2017
227×9×9×9 × (6×9×9×9×9×9×9×9×9+3) × (7×7×7×7×9×9×9+7)2306950757570596032Found by Marc Lapierre, 2017
239 × (8×8×8×9×9×9×9×9×9×9–1) × ((7×9×9–2)×9×9×9×9×9×9–3)6617798452548977166Found by Marc Lapierre, 2017
249×9×9×9×9 × (7×9×9×9×9×9×9–8) × ((6×8×8×8×8×8+5)×8×9×9+1)9539972462642799359Found by Marc Lapierre, 2017

Question #2:

No one has yet found any other palindromes which are the product of 3 or more consecutive integers. Patrick De Geest showed that there are no such products less than 6×1029. Ulrich Schimke searched products of 3 consecutive integers up to 8×1015. Andrew Bayly searched for products up to 109.

Brendan Owen explained why no palindrome is the product of 5 or more consecutive integers: because one of these will be divisible by 5, and another will be divisible by 2, making the palindrome end in 0, an impossibility. Using similar reasoning, he showed that any palindrome which is the product of 4 consecutive integers ends in 4, and any palindrome which is the product of 3 consecutive integers ends in 4 or 6. Bayly also made the latter observation.

Joseph DeVincentis showed that any palindrome which is the product of 4 consecutive integers ends in "024".

Several similar questions are investigated at this page of Patrick De Geest.

Question #3:

Let P(a,b) be the smallest palindrome in base a and b.

Ulrich Schimke showed that P(a,a+1)=2a2+3a+2 for a≥4. The sequence P(a,a+1): 6643, 10, 46, 67, 92, 121, . . . is now sequence A048268 of the Encyclopedia of Integer Sequences.

Schimke also showed that P(a,a+2)=(3a2+6a+2)/2 for even a≥8, and (a2+4a+3)/2 for odd a≥5. The sequence P(a,a+2): 5, 26, 21, 24, 154, 40, 121, 60, 181, 84, 253, 112, . . . is now sequence A048269 of the Encyclopedia of Integer Sequences. He believes that there are polynomials for every P(a,a+n).

Joseph DeVincentis and Ulrich Schimke note that if b is a power of a, then b+1 is a palindrome in base a and b. Schimke notes that this is enough to show that for every n, there is a number which is a palindrome in at least n different bases. Schimke also generalizes this to note that if b is a palindrome in base a, then the smallest palindrome in bases a and b-1 is b.

Matt Galati gave the smallest palindromes in bases a and b for a,b≤35. DeVincentis did this for a,b≤10. Schimke points out the largest P(a,b) for a,b≤35 is P(7,35)=16008.

It is surprising that P(2,3)=6643 is so large. DeVincentis has some explanations for this. Schimke has calculated that the only numbers less than 4.5×107 that palindromic in base 2 and 3 are 6643, 1422773, and 5415589.

Here are the smallest palindromes in two given bases:

Smallest Palindromes in 2 Bases

a \ b234567 8910111213141516171819
36643
4510
5312646
67282167
7858852492
8 91216318154121
9 12710101098040154
10 33121558855121121191
11 25524425512166243660232
12 65136526104786591181277
13 313284298142351547022284326
14 15121015408135135453032360253379
15 693161265161280163168082848241112436
16 176817119385851701363532211172170337497
17 341784341181211307185282523629012690144562
18 32517333857209573252091711331462209323361433631
19 38120514428804026020666603621406080514180704
20 21160421126211944632732528476142105421273126541781

Question #4:

Joseph DeVincentis and Ulrich Schimke proved that there are infinitely many numbers which are not the sum of two palindromes, namely 2×10n+1 for n≥1. Each of these is too small to be the sum of two palindromes of length n+1, and too large to be the sum of two palindromes of length n, so can only be the sum of a palindrome of length n and a palindrome of length n+1 starting and ending with 1. But this means the palindrome of length n must end in 0, an impossibility.

The sequence of positive integers which are not the sum of two palindromes: 21, 32, 43, 54, 65, 76, 87, 98, 201, 1031, 1041, 1042, 1051, 1052, 1053, 1061, 1062, 1063, 1064, 1071, 1072, 1073, 1074, 1075, 1081, 1082, 1083, 1084, 1085, 1086, 1091, 1092, 1093, 1094, 1095, 1096, 1097, 1099, 1101, 1103, 1104, 1105, 1106, 1107, 1108, . . . is sequence A035137 of the Encyclopedia of Integer Sequences.

John Hoffman searched for numbers that were not the sum of 3 palindromes. He found none less than 9×108. He also notes all sufficiently large numbers seem to be the sum of 3 palindromes, one of which is the biggest or second biggest possible.

Hoffman notes that an integer n is the sum of at most 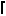log2 log10 n palindromes.

Hoffman also asks the following question: For what values of θ does ∑ nθ converge, where the sum is over palindromes n? The answer is for θ<–½.

DeVincentis showed that if a positive integer n with d digits is expressible as the difference of two palindromes, it is expressible as the difference of two palindromes each having no more than 2d-1 digits. He also showed that the smallest number that is not the difference of palindromes is 1020.

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 10/12/17.