Problem of the Month
(July 2009)

Take a polyomino and assign a weight of 1 or 2 to each square to get a weightomino. We are interested in rectangle tilings of overlapping weightominoes so that the total weight on each square is the same. We represent these weightominoes with line diagrams, with small dots representing weight 1 and large dots representing weight 2. Note that weightominoes can be rotated and reflected, but they are not equivalent to the corresponding polycubes. What are the orders of the small weightominoes? What if weights 1, 2, and 3 are allowed?

ANSWERS

If all the weights in the weightomino are the same size, then this usually reduces to the well known problem of tiling polyominoes. Thus we focus on the weightominoes with varying weights.

Here are the best known solutions for the 2-weightominoes and 3-weightominoes.

WeightominoOrderConfiguration
2
2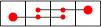
none
2
none
(Joe DeVincentis)
WeightominoOrderConfiguration
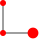2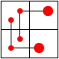
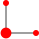2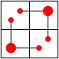
4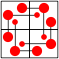
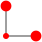4

Here are the best known solutions for the 4-weightominoes. We did not include the square 4-weightominoes because they can all tile a 2×2 square with 2 or 4 rotated copies (and the pictures are quite messy).

WeightominoOrderConfiguration
2
32
(George Sicherman)
2
2
none
none
(Joe DeVincentis)
2
32
(George Sicherman)
none
4
648×10×4
(George Sicherman)
none
8
4
2
3844×14×48
(Joe DeVincentis)
16
(George Sicherman)
24
(George Sicherman)

WeightominoOrderConfiguration
12
4
6
12
(George Sicherman)
2
4
2
4
4
4
12
(George Sicherman)
12
(George Sicherman)
12
(George Sicherman)
24
(George Sicherman)
4
?
8
none
none
2
14412×14×6
(George Sicherman)
968×14×6
(George Sicherman)

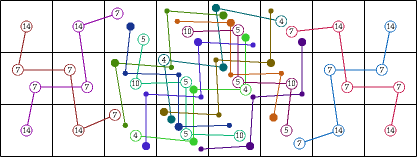
Here are the best known solutions for the 5-weightominoes with weight 6.

WeightominoOrderConfiguration
2
605×12×6
(George Sicherman)
?
12
(George Sicherman)
4
(George Sicherman)
4
6
(George Sicherman)
8
(George Sicherman)
4
(George Sicherman)
8010×12×4
(George Sicherman)
16
(George Sicherman)
?
4
4
(George Sicherman)
12
(George Sicherman)
8
(George Sicherman)
8
(George Sicherman)
4
4
4
2
none
none

WeightominoOrderConfiguration
16
(George Sicherman)
12
(George Sicherman)
24
(George Sicherman)
4
(George Sicherman)
15613×18×4
(George Sicherman)
none
?
none
(Bryce Herdt)
none
none
none
12
(George Sicherman)
24
(George Sicherman)
none
none
none
none
1126×14×8
(George Sicherman)
2
24
(George Sicherman)
2
2
none

Here are the best known solutions for some of the 5-weightominoes with weight 7.

WeightominoOrderConfiguration
2
(George Sicherman)
50
(George Sicherman)
1446×21×8
(George Sicherman)
none
(Joe DeVincentis)
14412×14×6
(George Sicherman)
none
(Bryce Herdt)
24
(George Sicherman)
20
(George Sicherman)
4
(George Sicherman)
24
(George Sicherman)
20
(George Sicherman)
20
(George Sicherman)
24
(George Sicherman)
24
(George Sicherman)
24
(George Sicherman)
12
(George Sicherman)
4
(George Sicherman)
24
(George Sicherman)
968×12×7
(George Sicherman)
48
(George Sicherman)
none
(Bryce Herdt)
?
32
(George Sicherman)
4
(George Sicherman)
48
(George Sicherman)
724×9×14
(George Sicherman)

WeightominoOrderConfiguration
12
(George Sicherman)
12
(George Sicherman)
12
(George Sicherman)
12
(George Sicherman)
8
(George Sicherman)
24
(George Sicherman)
4
(George Sicherman)
28
(George Sicherman)
8
(George Sicherman)
32
(George Sicherman)
4
(George Sicherman)
24
(George Sicherman)
48
(George Sicherman)
24
(George Sicherman)
727×12×6
(George Sicherman)
16
(George Sicherman)
16
(George Sicherman)
12
(George Sicherman)
6
(George Sicherman)
19614×14×7
(George Sicherman)
none
(Bryce Herdt)
6
(George Sicherman)
12
(George Sicherman)
12
(George Sicherman)
12
(George Sicherman)
12
(George Sicherman)
none
(Bryce Herdt)
30
(George Sicherman)
?
40
(George Sicherman)
16
(George Sicherman)
16
(George Sicherman)

George Sicherman also found these pentominoes with weight 7 tiled:

Here are the small polyominoes that cannot tile a rectangle, but can as weightominoes:

PolyominoWeighted
Order		Configuration
8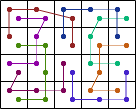
(Bryce Herdt)
8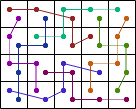
(George Sicherman)
24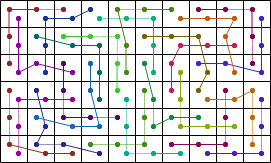
(George Sicherman)
16020×20×2
(George Sicherman)
4
(George Sicherman)
4
(George Sicherman)
8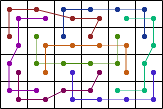
(Joe DeVincentis)
12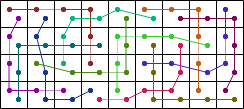
(George Sicherman)
16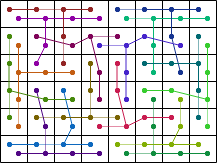
(George Sicherman)
28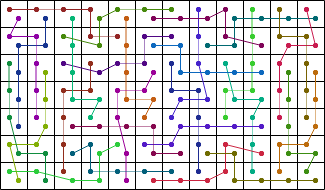
(George Sicherman)
48
(George Sicherman)
9616×18×2
(George Sicherman)
12010×18×4
(George Sicherman)
8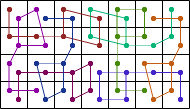
(George Sicherman)
12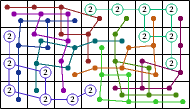
(George Sicherman)
12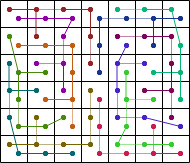
(George Sicherman)
20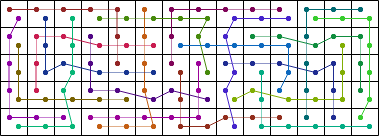
(George Sicherman)
20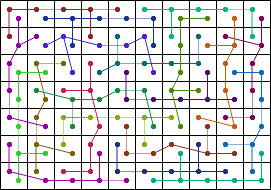
(George Sicherman)
24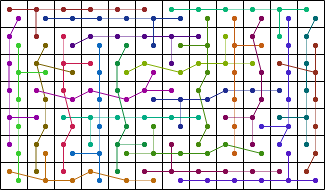
(George Sicherman)
24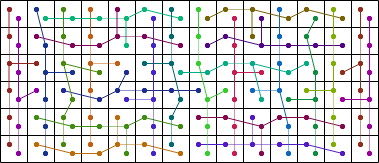
(George Sicherman)
24
(George Sicherman)
30
(George Sicherman)
30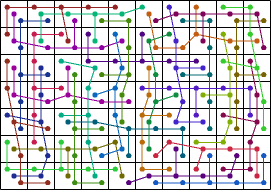
(George Sicherman)
32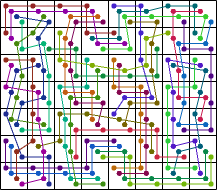
(George Sicherman)
32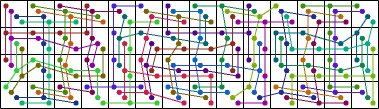
(George Sicherman)
32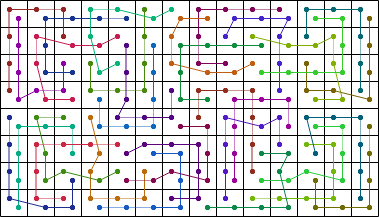
(George Sicherman)
32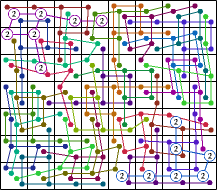
(George Sicherman)
36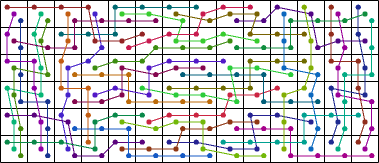
(George Sicherman)
40
(George Sicherman)
48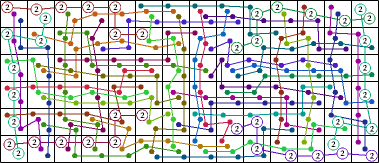
(George Sicherman)
48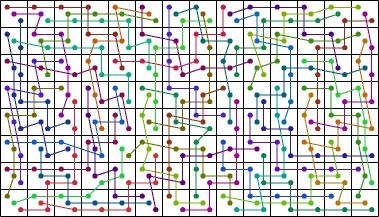
(George Sicherman)
549×14×3
(George Sicherman)
6010×14×3
(George Sicherman)
6014×15×2
(George Sicherman)
7212×14×3
(George Sicherman)
8010×14×4
(George Sicherman)
8811×14×4
(George Sicherman)
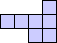9612×14×4
(George Sicherman)
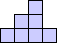9612×14×4
(George Sicherman)
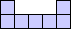10010×14×5
(George Sicherman)

Bryce Herdt showed that all C polyominoes with an even number of squares tile rectangles as weightominoes.

Here are the small polyominoes that have smaller orders as weightominoes:

PolyominoOrderWeighted
Order		Configuration
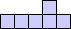9220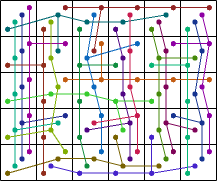
(George Sicherman)
286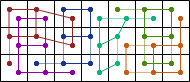
(George Sicherman)
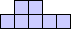7616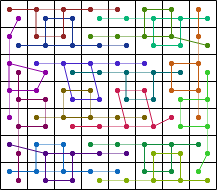
(George Sicherman)
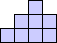24636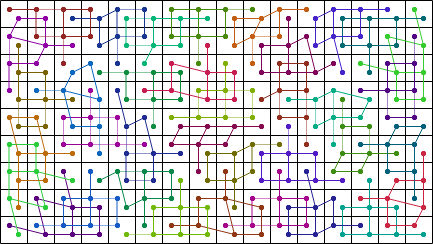
(George Sicherman)
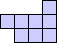1806012×20×2
(George Sicherman)

Bryce Herdt told me about this page by Alexandre Owen Muniz, where he defines weightominoes, which he calls sumominoes.

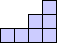
Bryce Herdt tiled all the weightominoes with total weight 4 into a rectangle:

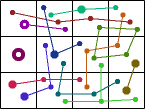
Alexandre Owen Muniz then asked whether there was a n-omino whose weightominoes with weight n+1 tiled some rectangle. Bryce Herdt found this solution.

George Sicherman extended the investigation to some weightominoes using weights 1-3:

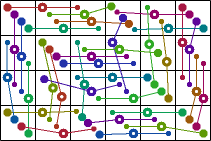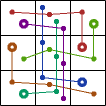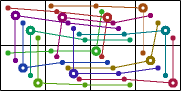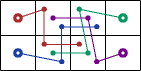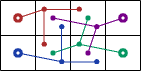Bryce Herdt noted that the unsolved 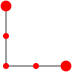can tile a 4×4 square with depth 21 if we allowed positive and negative copies of the polyomino!

George Sicherman then showed that 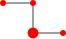can tile a 4×4 square with depth 10 and 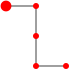can tile a 4×4 square with depth 18 allowing negative copies.

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 7/31/09.