1
| 2
| 12
| 3
| 13
| 23
| 123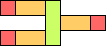
| 4
14 | 
24 | 
124 | 
34 | 
134 | 
234 | 
1234 | 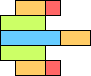
5 | 
|
Jeremy Galvagni showed that every integer k has at least one solution. In particular, a 1×k2 rectangle can be surrounded by k2 non-touching copies of a 1×k rectangle.
Here are the smallest known configurations for integer values of k:
|
Joe DeVincentis showed that the only numerical configurations where area 6 is the largest area are the ones shown below:
6
| 36
| 246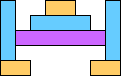
| 123456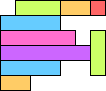
|
And then he proved that all such solutions for the k=2 case are just scaled up versions of one of the solutions above. Thus only area sets that are multiples of {1}, {1,2}, {1,2,3}, {1,2,3,4}, and {1,2,3,4,5,6} are possible!
|
|
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
|
| |||||||||
| |||||||||
| |||||||||
| |||||||||
| |||||||||
|
|
|
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
|
|
|
|
|
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
|
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
|
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 11/21/19.