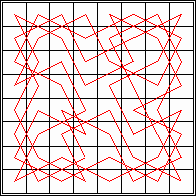

This month, we investigate trivial knight tours (TNTs), knight tours with the property that the only squares on the tour which are a knight's move apart are neighbours on the tour. Thus after the first knight move, all further knight moves in the loop are determined. The problem is to find the longest such tour for a given board.
Jonathan Welton, who suggested this problem, has found TNTs on square chessboards from 3×3 to 10×10, and shown them to be maximal by exhaustive search:
 length 8 | 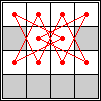 length 10 | 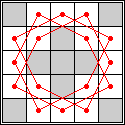 length 16 | 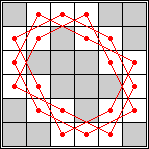 length 20 | 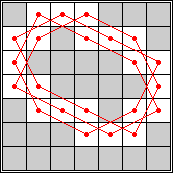 length 22 |
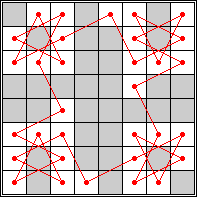 length 32 | 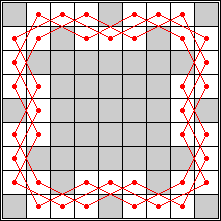 length 40 | 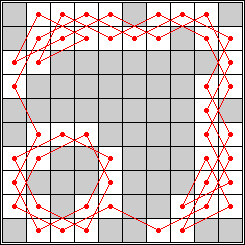 length 48 |
What are the maximal TNTs on larger square boards? What about rectangular boards? What about paths instead of cycles?
What are the maximal trivial tours for other chess pieces: rooks, bishops, kings, and queens? What about other "fairy chess" pieces?
| m \ n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|
| 3 | 8 | |||||||
| 4 | 10 | 10 | ||||||
| 5 | 10 | 10 | 16 | |||||
| 6 | 10 | 10 | 16 | 20 | ||||
| 7 | 12 | 14 | 16 | 22 | 22 | |||
| 8 | 14 | 16 | 18 | 22 | 26 | 32 | ||
| 9 | 14 | 18 | 20 | 28 | 30 | 34 | 40 | |
| 10 | 18 | 20 | 22 | 32 | 34 | 38 | 44 | 48 |
| 11 | 18 | 22 | 24 | 34 | 38 | 42 | ||
| 12 | 22 | 22 | 28 | 34 | 40 | |||
| 13 | 22 | 26 | 30 | 40 | ||||
| 14 | 24 | 28 | 30 | 44 | ||||
| 15 | 26 | 30 | 32 | 46 | ||||
| 16 | 28 | 30 | 36 | |||||
| 17 | 30 | 32 | 38 | |||||
| 18 | 32 | 36 | 40 | |||||
| 19 | 34 | 38 | ||||||
| 20 | 36 | 40 |
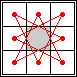
Here are the smallest known 3-regular and 4-regular realizations for knights:
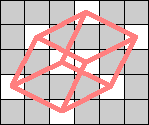 (Tino Jonker) | 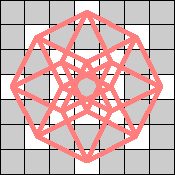 (Tino Jonker) |
In 2009, Jonathan Welton found the disjoint tours below that have 24 knights on a 7×7 board and a 4×12 board:
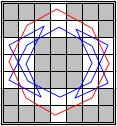 | 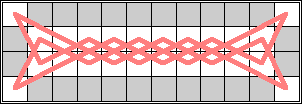 |
Queens
| m \ n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0 | 3 | ||||||||
| 3 | 3 | 4 | 4 | |||||||
| 4 | 3 | 4 | 4 | 6 | ||||||
| 5 | 3 | 4 | 6 | 6 | 7 | |||||
| 6 | 3 | 4 | 6 | 8 | 8 | 9 | ||||
| 7 | 3 | 4 | 6 | 8 | 9 | 10 | 11 | |||
| 8 | 3 | 4 | 6 | 8 | 10 | 11 | 12 | 13 | ||
| 9 | 3 | 4 | 6 | 8 | 10 | 12 | 13 | 14 | 14 | |
| 10 | 3 | 4 | 6 | 8 | 10 | 12 | 14 | 14 | 16 | 16 |
| 11 | 3 | 4 | 6 | 8 | 10 | 12 | 14 | 15 | 16 | |
| 12 | 3 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
Ed Pegg suggested that we look for other graphs besides cycles, the only connected 2-regular graphs. The next natural candidates are the disconnected 2-regular graphs. Here are the smallest known boards that a queen can realize for the disconnected 2-regular graphs of size 6 through 9.
| 6 | 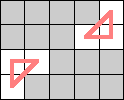 (Dave Langers) | 7 | 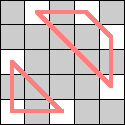 (Dave Langers) | 8 | 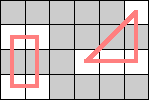 (Dave Langers) | 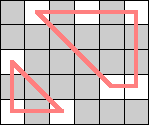 (Dave Langers) |
| 9 |  (Dave Langers) | 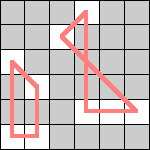 (Dave Langers) | 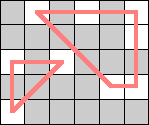 (Dave Langers) |
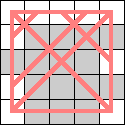
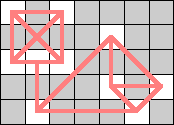
Here are the smallest known boards that a queen can realize for the 3-regular graphs of size 4, 6, 8, and 10. Can anyone improve these?
| 4 |  | 6 |  |  (Dave Langers) |
| 8 | 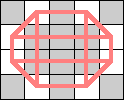 |  (Dave Langers) | 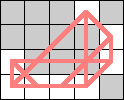 (Dave Langers) |  (Dave Langers) | 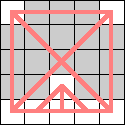 (Dave Langers) | 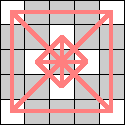 (Dave Langers) |
| 10 | 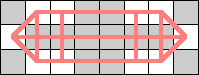 | 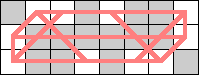 | 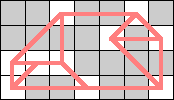 | 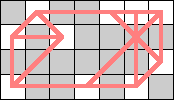 |
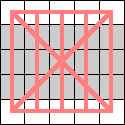 | 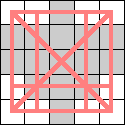 | 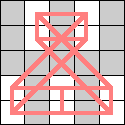 (Dave Langers) | 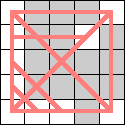 (Dave Langers) | 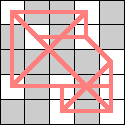 (Dave Langers) |
 (Dave Langers) | 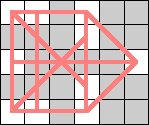 (Daniele Degiorgi) | 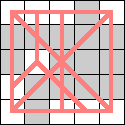 (Dave Langers) | 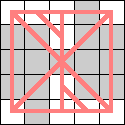 (Dave Langers) | 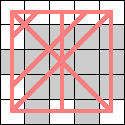 (Dave Langers) |
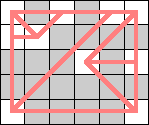 (Dave Langers) | 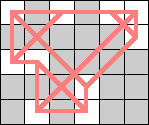 (Dave Langers) | 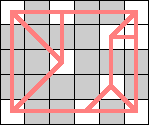 (Dave Langers) | 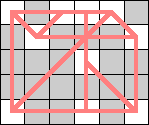 (Dave Langers) |
 (Dave Langers) | 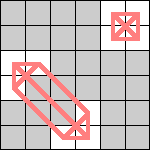 (Dave Langers) | 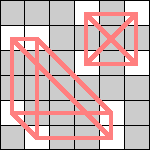 (Dave Langers) |
Here is the smallest known realization for the Heawood graph, and the dodecahedron graph:
 (Geoff Exoo) | 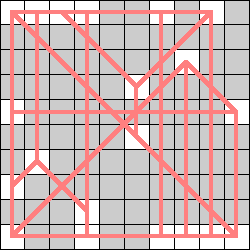 (Geoff Exoo) |
Geoff Exoo showed that all 3-regular graphs with 14 vertices can also be realized by queens. I conjecture that all 3-regular graphs can be realized this way.
Here is the smallest known 4-regular realization for queens, and the smallest known realization for the 4-cube. What are some other 4 regular graphs?
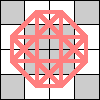 | 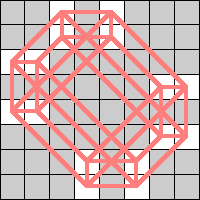 (Geoff Exoo) |
Dave Langers asks "For small n, what is the smallest board that contains a cycle of winding number (the number of revolutions you turn while you follow the cycle) n?"
Kings
On an n×n chessboard, the maximum tours are apparently vertical zig-zags, and have length 2(n–5)⌊(n+5)/4⌋ + 12, for n≥4. Can anyone prove this? What is the formula for an m×n chessboard?
Kings have a trivial 3-regular configuration on a 2×2 board, but the next smallest connected 3-regular graph I found was on a 7×5 board. Is there one in between these two? It's clear that kings can only produce planar regular graphs.
 | 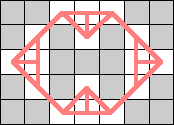 |
The problem for bishops is easier. On an m×n chessboard, the maximum tour apparently has length 2n–4, for m=n≥4, and 2(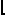 (m–1)/4
(m–1)/4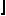 +
+ 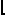 (n–1)/4
(n–1)/4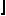 ) if m≠n. Can anyone prove this? It is easy to prove that bishops do not admit 3-regular configurations.
) if m≠n. Can anyone prove this? It is easy to prove that bishops do not admit 3-regular configurations.
Rooks
The problem for rooks is trivial. On an m×n chessboard, the maximum tour has length 2 min{m,n}, and each optimal tour either contains 2 rooks in each row or 2 rooks in each column. Rooks also do not admit 3-regular configurations.
Amazons
| Amazons move either like a queen or knight. | 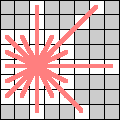 |
Tour of m × n Rectangles
|
| Archbishops move either like a bishop or knight. | 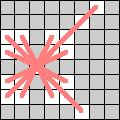 |
Tour of m × n Rectangles
|
| Empresses move either like a rook or knight. | 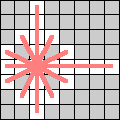 |
Tour of m × n Rectangles
|
| Fivers move to a square exactly 5 units away, either 5 squares horizontally or vertically, or as the hypotenuse of a 3-4-5 triangle. | 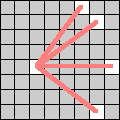 |
Tour of m × n Rectangles
|
| Squirrels move 2 squares either horizontally or vertically, and 0, 1, or 2 squares in a perpendicular direction. | 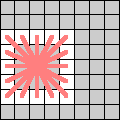 |
Tour of m × n Rectangles
|
| Zebras move 3 squares either horizontally or vertically, and 2 squares in a perpendicular direction. | 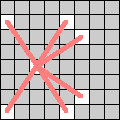 |
Tour of m × n Rectangles
|
| Giraffes move 4 squares either horizontally or vertically, and 1 square in a perpendicular direction. | 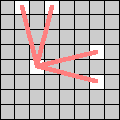 |
Tour of m × n Rectangles
|
| Double Kings make 2 king moves. | 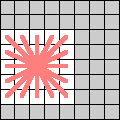 |
Tour of m × n Rectangles
|
| Sparklers move either 1 space horizontally or vertically, or 2 spaces diagonally. | 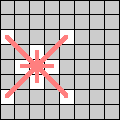 |
Tour of m × n Rectangles
|
| Oxen move 3 spaces horizontally or vertically, and 0 or 1 spaces in a perpendicular direction. | 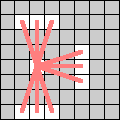 |
Tour of m × n Rectangles
|
Guenter Stertenbrink found a piece (that moves distance √5 or √8) that can realize the Petersen Graph on a 4×4 board:
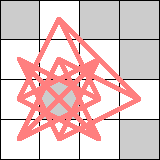
What are best solutions for paths rather than cycles?
When is it possible to cover a board with distinct trivial tours? What is the smallest number of tours that suffices?
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 6/7/09.