Problem of the Month (August 2008)

This month we consider tiling the lines of an n×m grid using the ten digits, as they usually appear on a digital clock. We are interested in the possible totals of the digits for a given m and n. Digits can intersect, and be rotated. Digits can not overlap, or be reflected. For small grids, what are the possible digit totals? For large grids, what are the smallest and largest possible totals?

ANSWERS

Here is a table of the smallest and largest possible totals for various m×n grids:

Smallest and Largest Known Totals for n×m Grids
n \ m0123
00 / 0
1φφ
21 / 14 / 86 / 18
3φφ9 / 3117 / 46
(BH/AS)
42 / 2φ5 / 44
(EF/DB)		?
5φ14 / 208 / 47?
63 / 3φ10 / 57?
7φ16 / 3413 / 70?
84 / 421 / 2715 / 87?
9φ20 / 4818 / 90?

Anti Solg and Bruce Herdt sent many 3×3 grids.

Luke Pebody showed that the smallest totals for large 1×n grids depend on n mod 3, and that the largest totals for large 1×n grids depend on n mod 2:

(3k)×1 grid with total 4k+8

(3k+1)×1 grid with total 4k+8

(3k+2)×1 grid with total 4k+12

(2k)×1 grid with total 7k-29

(2k+1)×1 grid with total 7k-8

Richard Sabey gave this small total tiling:

(4j+1)×(4k+2) grid with total 4jk+11j+28k+4

Luke Pebody found this group of 7's that tiles the plane, giving him hope that for large m×n grids, a total on the order of 7(2mn+m+n)/3 is possible:
repeatable tile built with 7's

David Bevan found the largest totals for 2n×4 and 4n×6 grids:

2n×4 grid with total 42n+2

4n×6 grid with total 114n+14

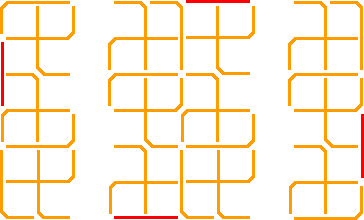The 0×n solutions are trivial. Here are the known 1×n solutions for small n:

1×2

4
8

1×5

14, 17, 20

1×7

16
20
22, 25

24
26, 29
28, 31, 34

1×8

21, 24, 27

1×9

20, 23
24, 27
26, 29, 32

30
34
36, 39

38
40, 43
42, 45, 48

Luke Pebody gave a full analysis of the 1×n possibilities, essentially agreeing with the following directed graph of mine:

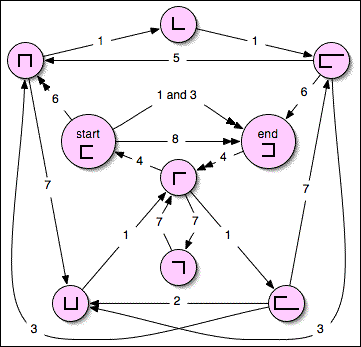
Here are the known 2×n solutions for small n:

2×2

6
7
10
11
12, 15, 18
17 (AS) (BH)

2×3

9
10
13
14

15, 18, 21
17, 20, 23
24
27
28, 31

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 8/12/08.