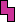







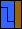








1. Given two polyominoes, what is the smallest (by area) rectangle that they tile, using at least one copy of each?
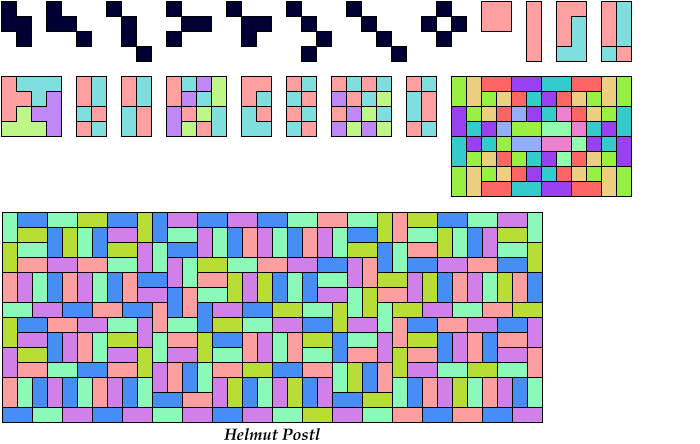
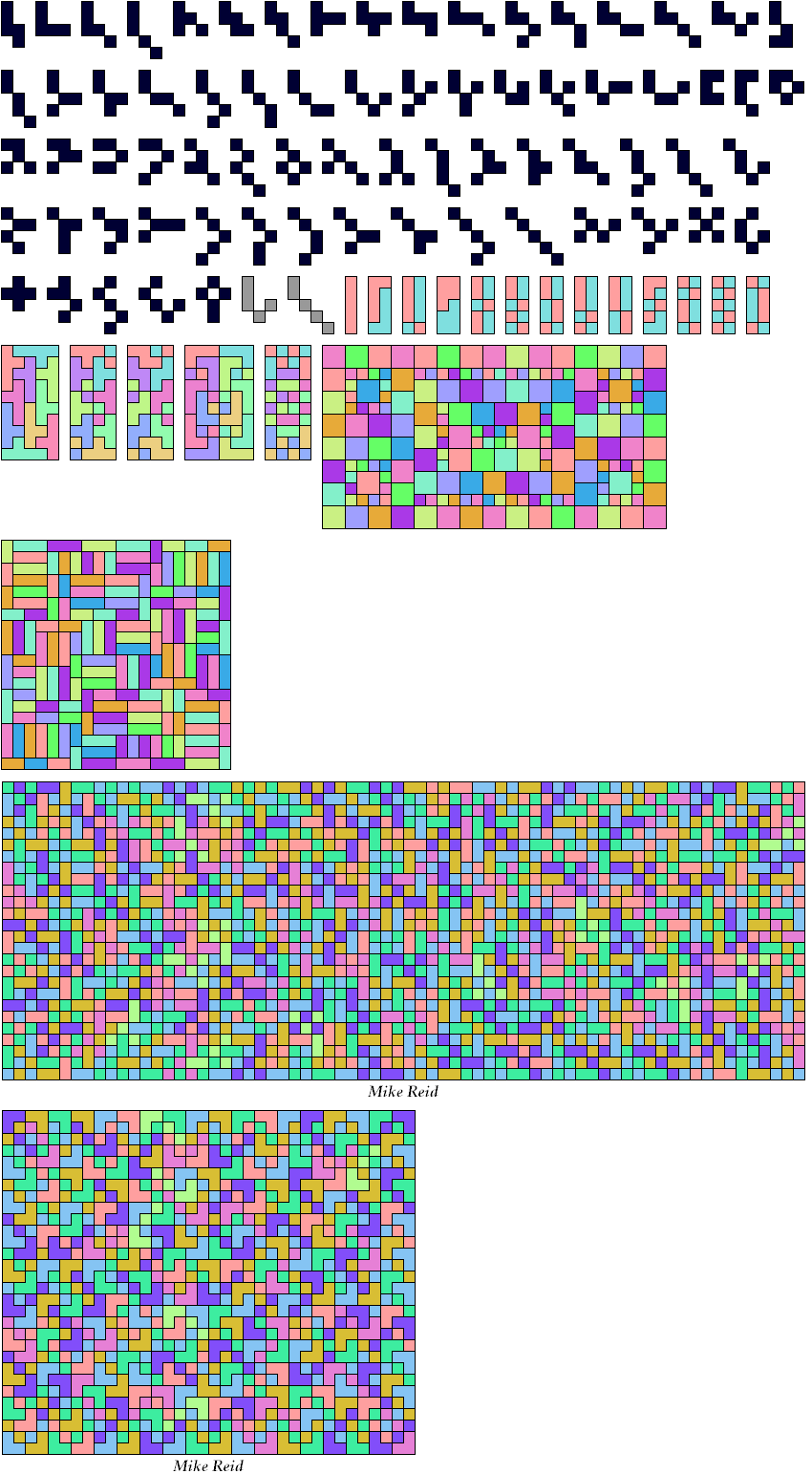
2. Given a polyomino reptile P, how many copies of P can be used to tile P?
3. Which polykings (vertex-connected unions of unit squares) are rectifiable (can tile a rectangle)?
4. Which polykings are reptiles? What are their orders? Are there polykings that are reptiles but not rectifiable?
1.
Rodolfo Kurchan let me know that this problem has been studied before, with most solutions by Mike Reid.
Below are the smallest-known rectangles containing pairs of polyominoes:
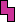
| 
| 
| 
| |
|---|---|---|---|---|

|  |  |  | 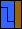
|

|  |  | 
| |

| none | 
| ||

| 
|
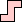
| 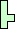
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |
|---|---|---|---|---|---|---|---|---|---|---|---|---|

|  |  (GS) | ? |  (GS) |  | 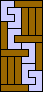 |  |  |  | 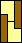 | 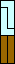 | 
|

|  |  |  |  | 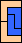 |  | 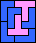 |  |  |  |  | 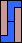
|

|  (GS) | 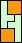 | none | none |  | none (GS) | 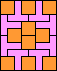 (GS) | 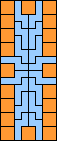 (GS) | none |  |  | 
|

|  |  |  |  |  |  |  |  |  |  |  | 
|
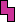
| none | 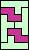 | none | none |  |  |  | none | none | 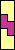 | 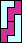 | 
|
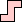
| 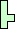
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |
|---|---|---|---|---|---|---|---|---|---|---|---|

| 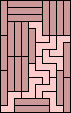 |  | ? | 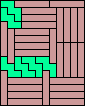 (GS) |  | 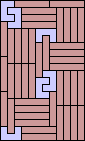 (GS) |  |  | 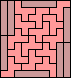 |  | 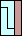
|

|  |  |  |  | 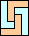 |  |  |  |  | 
| |

| 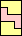 | 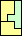 |  |  | 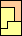 |  |  |  | 
| ||

| none |  | none | none |  | 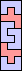 | none | none | |||

| none |  | none | none |  |  | 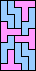
| ||||

| none | 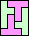 | none |  | none |  (Mike Reid) | |||||

| none |  |  | none |  (Mike Reid) | ||||||

| 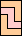 | 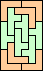 | none |  (Mike Reid) | |||||||

| none | 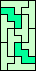 | none | ||||||||

| none | 
| |||||||||
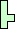
| 
|

| 
| 
| 
| 
| 
| 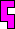
| 
| 
| 
| 
| 
| |
|---|---|---|---|---|---|---|---|---|---|---|---|---|

|  | 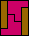 |  |  | 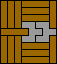 (GS) |  | 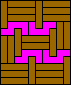 (GS) | 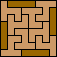 |  |  |  | 
|

|  |  |  |  |  |  | 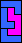 | 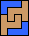 |  |  |  | 
|

|  |  |  |  | none (JD) |  | none (MR) | none (MR) |  | none (MR) | none (JD) | none (MR) |

|  |  |  |  |  |  |  |  |  |  |  |  (GS) |
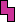
| 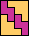 |  |  |  | none (JD) |  |  | 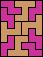 |  (GS) | none (JD) | none (JD) | none (JD) |

| 
| 
| 
| 
| 
| 
| 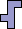
| 
| 
| 
| 
| |
|---|---|---|---|---|---|---|---|---|---|---|---|---|

| 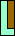 |  |  |  |  |  |  | 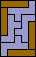 |  |  | 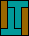 | 
|

|  |  |  |  |  |  |  |  |  |  |  (GS) | 
|

|  | none (MR) | none (MR) |  |  | none (MR) | none (MR) | none (MR) | none (JD) | none (JD) |  | 
|

|  |  |  (GS) |  |  |  |  |  |  |  |  | 
|
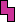
| 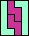 | none (JD) | none (JD) |  (GS) | 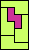 | none (JD) | none (JD) | none (JD) | none (JD) | none (JD) |  (GS) | 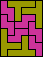
|
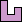
| 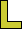
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |
|---|---|---|---|---|---|---|---|---|---|---|---|

| 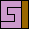 |  |  |  |  | 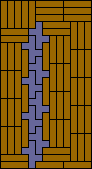 (MR) | 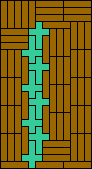 (MR) |  |  |  | 
|

|  |  | 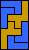 |  |  |  |  |  |  |  | 
|

|  |  | 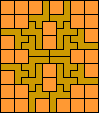 (GS) | none (MR) | none (MR) | none (MR) | none (MR) |  |  | none (MR) | 
|

|  |  | 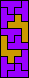 |  |  |  (GS) | ? | 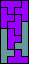 |  |  (GS) |  (GS) |
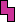
|  | 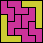 | none (JD) | none (JD) | none (JD) | none (JD) | none (JD) |  |  | none (JD) | none (JD) |
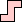
| 
| 
| 
| 
| 
| |
|---|---|---|---|---|---|---|

|  (GS) |  |  (MR) |  | 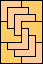 | 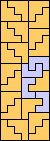 (GS) |

|  (GS) |  |  (GS) |  |  | 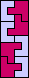
|

|  (GS) |  | none (GS) |  (GS) | 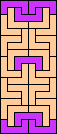 (GS) | 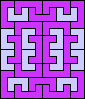 (GS) |

| 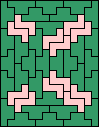 (GS) |  |  (GS) |  | 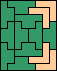 |  (GS) |

| none (JD) |  | none (JD) | none (JD) | none (GS) | none (JD) |

| 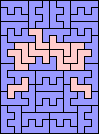 (MR) |  |  |  | 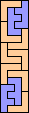 | 
|
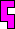
|  (MR) |  | none (GS) | none (GS) |  (MR) | none (GS) |

| none (GS) | 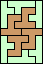 | none (JD) | none (GS) | 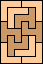 | none (JD) |

|  (GS) |  | ? |  (GS) |  (MR) | 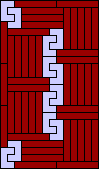 (MR) |

| none (JD) |  | none (JD) | none (JD) |  (GS) | 
|

| none (JD) |  | none (GS) | none (JD) | none (GS) |  (GS) |

| none (JD) |  | none (JD) | none (JD) |  (GS) | none (JD) |

| 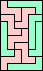 (MR) |  |  (GS) |  | 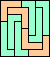 | 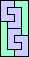
|

| none (JD) |  | none (JD) | none (JD) |  (GS) | none (GS) |

| none (JD) |  | none (JD) | none (JD) |  (MR) | none (JD) |

|  |  | none (JD) |  | 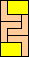 | 
|
|  |  |  (GS) |  |  | 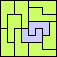
|

| none (JD) |  | none (JD) | none (JD) |  | none (JD) |

| none (JD) |  | none (JD) | none (JD) |  |  (GS) |
| none (JD) | 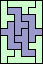 | none (JD) | none (JD) |  (GS) |  (GS) |

| none (JD) |  | none (JD) | none (JD) | 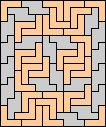 (GS) |  (GS) |

| none (JD) |  | none (JD) | none (JD) | none (GS) | none (JD) |

| none (GS) |  | none (JD) |  | none (GS) | 
|

|  (GS) |  | none (GS) |  (GS) | none (GS) |  (GS) |
|  |  | none (MR) |  | 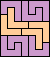 | 
|
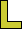
|  (GS) |  | none (GS) |  |  | 
|

| none (JD) | 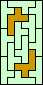 | none (JD) | none (JD) | none (GS) |  (GS) |

| none (JD) |  | none (JD) | none (JD) |  (GS) | none (JD) |

| none (JD) |  | none (JD) | none (JD) |  (GS) | none (JD) |

| none (JD) |  | none (JD) | none (JD) | none (GS) | none (JD) |

| none (GS) |  (GS) | none (JD) | none (GS) | none (GS) |  (MR) |

|  | 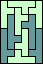 |  (GS) |  | 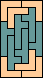 | 
|

|  (MR) |  | none (GS) |  (GS) | 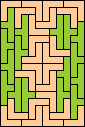 (GS) | 
|

| none (JD) | 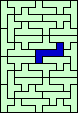 (GS) | none (JD) | none (JD) | none (GS) | none (JD) |

| none (GS) |  | none (GS) | none (GS) |  |  (GS) |

| 
| 
| 
| 
| 
| |
|---|---|---|---|---|---|---|

| 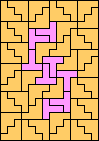 (GS) |  |  |  | 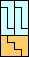 | 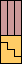
|

|  (GS) |  |  (GS) |  | 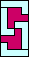 | 
|

| none (JD) |  | 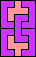 |  |  | 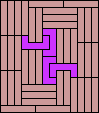 (GS) |

| 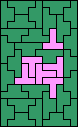 (GS) |  |  |  |  | 
|

| none (JD) | none (JD) | none (JD) |  |  | 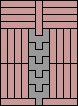 (JD) |

|  (GS) |  |  |  |  | 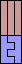
|
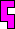
| none (JD) |  (GS) |  |  | 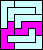 | 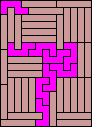 (GS) |

| none (JD) | 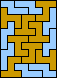 | none (JD) |  | 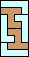 | 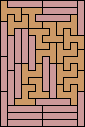 (GS) |

|  | 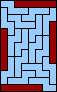 |  |  |  | 
|

|  | none (JD) | none (JD) |  |  | 
|

| none (JD) | none (JD) | none (JD) |  |  |  (GS) |

| none (JD) | none (JD) | none (JD) |  |  | 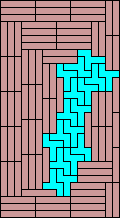 (MR) |

| 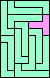 |  |  | 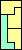 |  | 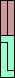
|

| none (JD) | none (JD) | none (JD) |  |  |  (GS) |

| none (JD) | none (JD) | none (JD) |  |  |  (GS) |

|  |  | 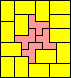 |  |  | 
|
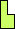
|  |  |  |  |  | 
|

|  (GS) | none (JD) | none (JD) | 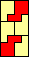 |  | 
|

| none (JD) | none (JD) | none (JD) |  |  | 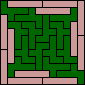 (GS) |
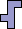
| none (JD) | none (JD) | none (JD) |  |  |  (GS) |

| 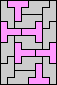 | none (JD) | none (JD) |  |  |  (GS) |

| none (JD) | none (JD) | none (JD) |  | 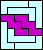 | 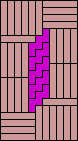 (GS) |

| none (JD) |  | none (JD) |  | 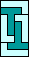 | 
|

| none (JD) |  |  (GS) | 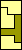 |  | 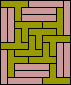 (GS) |
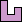
|  |  |  | 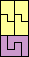 | 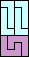 | 
|
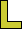
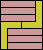
|  |  |  |  |  | 
|

| none (JD) | none (JD) | none (JD) |  | 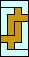 | 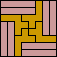
|

|  (GS) | none (JD) | none (JD) |  |  | 
|

| none (JD) | none (JD) | none (JD) |  | 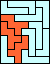 | 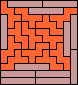 (GS) |

| none (JD) | none (JD) | none (JD) |  |  | ? |

| none (JD) | none (GS) | none (GS) |  |  |  (MR) |

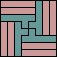
| 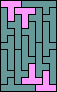 |  |  | 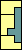 |  | 
|

|  (GS) | 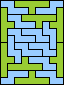 |  |  |  | 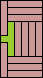
|

| none (JD) | none (JD) | none (JD) |  |  | ? |

| none (JD) | none (GS) | none (GS) |  | 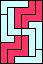 | 
|
George Sicherman and Patrick Hamlyn sent hex-hex and hept-hept pictures. George has more pictures, which are color-coded and have areas, while Patrick's tilings are all minimal. George's hex-hex pictures are here and here, while Patrick's are here. George's hept-hept pictures are here, here, and here, while Patrick's are here.
George Sicherman also sent 1 tet-hept picture, 1 2 pent-hept pictures, 1 2 3 4 5 6 7 8 pent-oct pictures, and 1 2 3 4 5 hex-hept pictures.
George Sicherman also investigated tiling tilted rectangles with two different polyominoes:
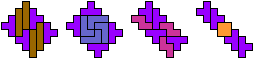
|

|

|

|

|

|
George Sicherman also investigated tiling a rectangle with two different polyaboloes:

| 
| 
| 
| 
| 
| |
|---|---|---|---|---|---|---|

| 
| 
| 
| 
| 
| 
|

| 
| none | 
| none | none | |

| 
| 
| 
| none | ||

| 
| 
| 
| |||

| 
| 
| ||||

| 
|

| 
| 
| 
| 
| 
| 
| |
|---|---|---|---|---|---|---|---|

| 
| ? | 
| 
| 
| 
| 
|

| 
| ? | 
| ? | none | none | 
|

| 
| ? | 
| ? | 
| none | 
|

| 
| 
| 
| 
| none | 
| 
|

| 
| ? | 
| ? | 
| none | 
|

| 
| 
| 
| 
| none | 
| 
|

| 
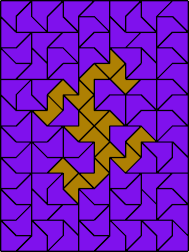
| 
| 
| 
| 
| 
| 
|

| 
| ? | 
| ? | none | none | 
|

| 
| ? | 
| 
| none | none | 
|

| 
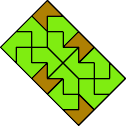
| 
| 
| 
| 
| 
| 
|

| 
| ? | 
| 
| none | none | none |

| 
| ? | 
| ? | none | none | 
|

| 
| ? | 
| ? | none | none | 
|

| 
| ? | 
| ? | none | none | 
|

| 
| 
| 
| 
| |
|---|---|---|---|---|---|

| 
| 
| 
| ? | 
|

| none | ? | ? | none | 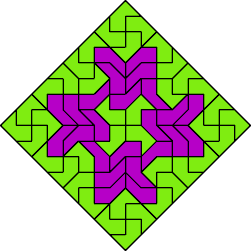
|

| ? | ? | ? | ? | 
|

| ? | 
| 
| 
| 
|

| none | ? | ? | ? | 
|

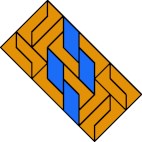
| 
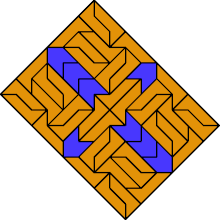
| 
| 
| 
| 
|

| ? |  |  | ? | 
|

| ? | ? | ? | ? | 
|

| ? | ? | ? | ? | 
|

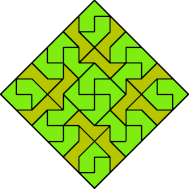
| ? |  |  | 
| |

| ? | ? | ? | ||

| ? | ? | |||

| ? |

| 
| 
| 
| 
| 
| 
| 
| |
|---|---|---|---|---|---|---|---|---|

| 
| 
| 
| 
| 
| 
| 
| 
|

| ? | ? |  |  | ? |  | 
| |

| ? | ? |  | 
| ? | ? | ||

| 
| 
| 
| 
| ? | |||

| none | none | ? | ? | ||||

| 
| 
| 
| |||||

| ? | 
| ||||||

| ? |
Here are the best-known impossible values for n for reptile polyominoes of area 6 or less:

| 
| 
| 
| 
| 
| 
| 2, 3, 5 | 4
| 6
| 8
|
 | 2, 3 | 4
| 5
| 6
|

| 
| 2, 3, 5, 8 | 4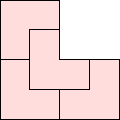
| 6
|
 | 2, 3, 5, 6 | 4 | 8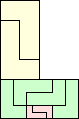 (AS) | 9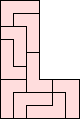 |
 | 2-15, 17, 18, 21 | 16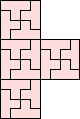 | 19 (JD) | 20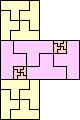 (JD) | 22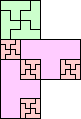 (JD) | 24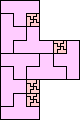 (JD) | 25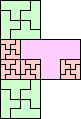 (JD) | 29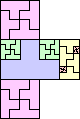 (MM) |
 | 2, 3, 5, 8 | 4
| 6
| 11
|
 | 2-9, 11, 12 | 10 | 13 (JD) | 14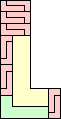 (MM) | 15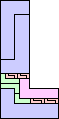 (AS) | 17 (MM) | 18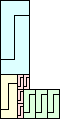 |
 | 2-11 | 12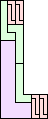 (JD) | 13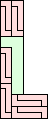 | 14 | 15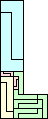 (AS) | 16 (MM) | 17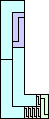 (AS) |
 | 2-8, 10, 12 | 9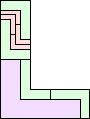 | 11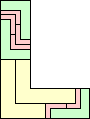 (AS) | 13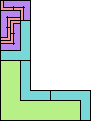 (GS) | 14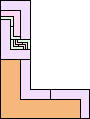 (AS) | 16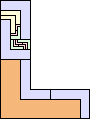 (AS) | 18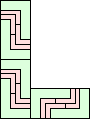 |
 | 2-17, 20-21, 25 | 18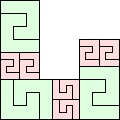 | 19 (GS) | 22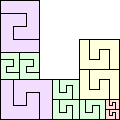 | 23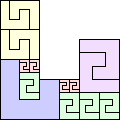 |
 | 2-7, 9-13, 16, 17 | 8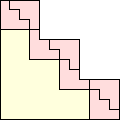 | 19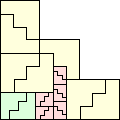 (JD) | 23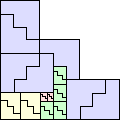 (MM) |
 | 2-29, 33, 35, 39 |
30 (GS) | 31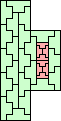 (AS) | 32 | 34 (MM) | 36 | 37 (MM) | 38 (MM) | 40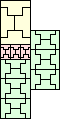 | 41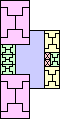 (MM) | 41 | 45 (JD) | 47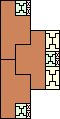 (JD) |
 | 2-21, 23-25, 27, 29, 31, 35 | 22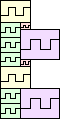 | 26 (JD) | 30 (MM) | 33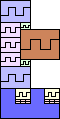 (JD) |
 | 2-39, 41, 42, 45, 47, 48, 50, 51, 53, 54, 57 |
40 | 43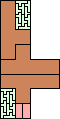 (JD) | 44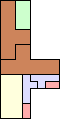 (JD) | 46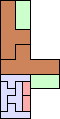 (JD) | 49 (JD) | 52 (AB) | 56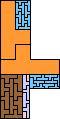 (MM) | 58 (AB) | 59 (MM) | 60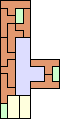 (JD) |
61 (AB) | 62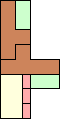 (JD) | 63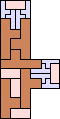 (JD) | 64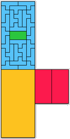 (AB) | 67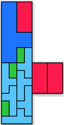 (AB) | 68 (AB) | 69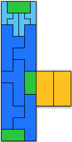 (AB) | 70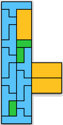 (AB) | 71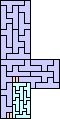 (MM) | 81 (MR) |
Andrew Bayly proved that this next polyomino can be tiled with 120 or more smaller copies!
 2-62, 64, 65, 67, 68, 70, 71, 73, 74, 76, 77, 79, 80, 82-119
2-62, 64, 65, 67, 68, 70, 71, 73, 74, 76, 77, 79, 80, 82-11963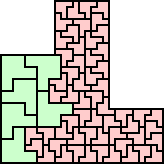 (LZ) | 66 (MR) | 69 (MR) | 72 (MR) |
75 (MR) | 78 (MR) | 81 (MR) |
 | ? | 888 (JD) |
 2-16, 18, 21
2-16, 18, 2117 (MR) | 19 (MR) | 20 (MR) | 22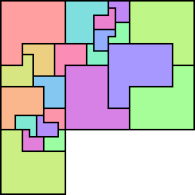 (MR) | 23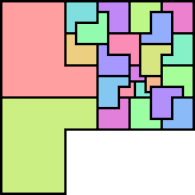 (MR) |
24 (MR) | 25 (MR) | 26 (MR) | 27 (MR) | 28 (MR) |
29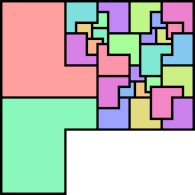 (MR) | 30 (MR) | 31 (MR) | 32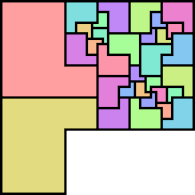 (MR) | 34 (MR) |
 2-16, 18, 19, 21, 24
2-16, 18, 19, 21, 2417 (MR) | 20 (MR) | 22 (MR) | 23 (MR) | 25 (MR) |
26 (MR) | 27 (MR) | 28 (MR) | 29 (MR) | 30 (MR) |
31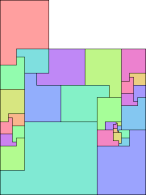 (MR) | 32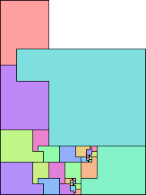 (MR) | 34 (MR) | 35 (MR) | 37 (MR) | 40 (MR) |
Here are the known rectifiable polykings (most by George Sicherman):
Here are the smallest known orders for non-polyomino reptile polykings:
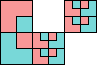
 order 4 |  order 10 (BH) | 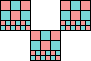 order 18 |
 order 4 | 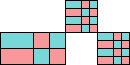 order 10 |  order 10 | 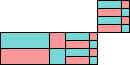 order 10 (MM) (AS) | 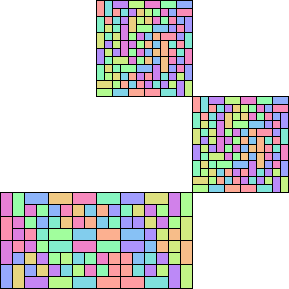 order 104 (GS) |
 order 10 (MM) (AS) |  order 16 (MM) (AS) | 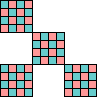 order 16 (MM) (AS) | 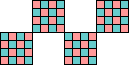 order 16 (MM) (AS) | |
 order 139 (AB) |  order 432 (GS) | |||
 order 13 (MM) |  order 17 (GS) | 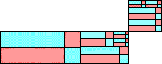 order 18 (MM) | 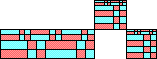 order 26 (MM) | 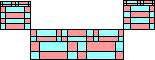 order 26 (MM) |
 order 28 (AS) |  order 28 (AS) |  order 28 (AS) |  order 34 (AS) |  order 34 (AS) |
 order 40 (AS) |  order 104 (MM) | 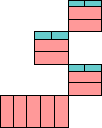 order 136 (MM) |  order 53 (GS) | |
 order 76 (GS) | ||||
 order 124 (GS) | 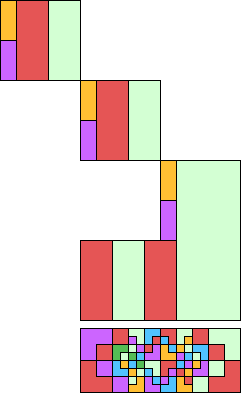 order 280 (GS) | |||
 order 104 (AB) |  order 1156 (GS) | |||
 order 280 (GS) | ||||
George Sicherman also investigated polymings:
 order 4 |  order 4 | 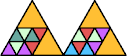 order 10 |  order 4 |  order 9 | 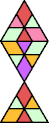 order 9 | 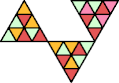 order 9 |  order 20 | 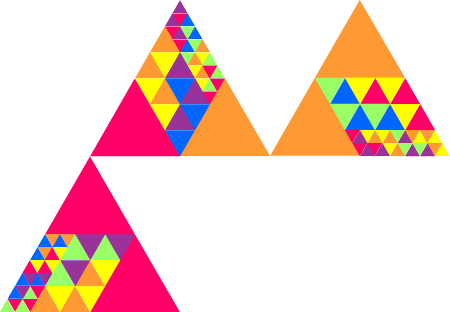 order 38 (BH) |
 order 4 |  order 4 | 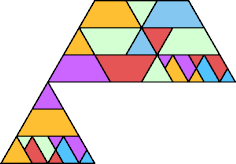 order 15 | 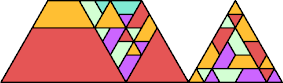 order 18 |  order 26 (BH) |
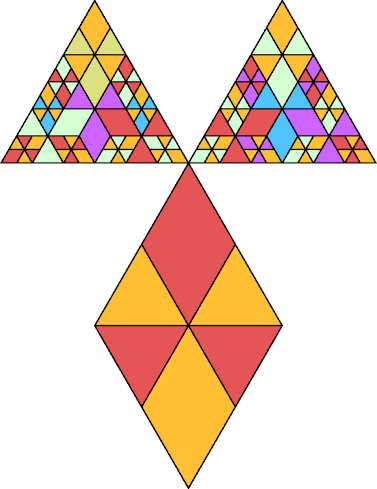 order 44 |  order 10 | 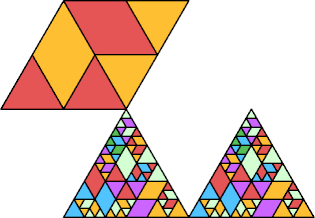 order 44 (GS) |
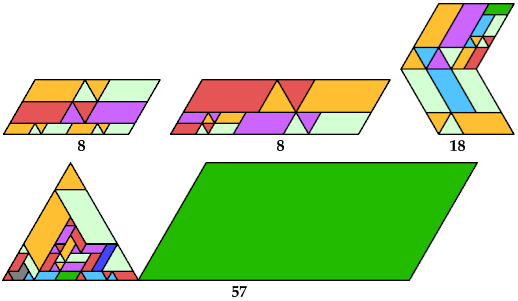 order 57 (GS) |
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 9/16/20.