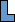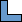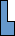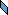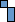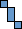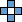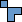Problem of the Month (August 2011)
1.
We call a polyomino P distinguishable if there are integers n, k, a, b, so that P is the only n-omino where a maximum of k copies of P can be packed in an a×b box. If P is distinguishable, we call the smallest such k the distinguishing mark of P.
Can you show that not all polyominoes are distinguishable? What is the smallest one? What are the distinguishing marks of some larger polyominoes? What about polyaboloes? What about polykings?
We call a polyomino P super-distinguishable if there are integers k, a, b, so that P is the only polyomino where a maximum of k copies of P can be packed in an a×b box. Which polyominoes are super-distinguishable?
We call a polyomino P 2-distinguishable if there are integers n, k1, a1, b1, k2, a2, b2, so that P is the only n-omino where a maximum of k1 copies of P can be packed in an a1×b1 box, and a maximum of k2 copies of P can be packed in an a2×b2 box. Which polyominoes are 2-distinguishable?
2.
For a given positive integer n, what is the smallest polyomino jigsaw puzzle in a square tray that has exactly n solutions, including rotations and reflections? (Here "smallest" means smallest tray, and of those, smallest number of pieces.) What are the solutions for rectangular trays?
ANSWERS
1.
Solutions were received from George Sicherman, Berend van der Zwaag, Andrew Bayly, David Wilson, Bryce Herdt, Gavin Theobald, and Patrick Hamlyn.
Berend van der Zwaag and George Sicherman showed that not all polyominoes are distinguishable.
Here are the known distinguishing marks of distinguishable polyominoes:
Small
Polyominoes
| Poly | Dist
|
|---|
 | 0 in 0×0
|  | 0 in 0×0
|  | 0 in 2×2
|  | 0 in 1×3
| |
|---|
| |
Tetrominoes
| Poly | Dist
|
|---|
 | 0 in 2×3
|  | 1 in 2×2
| 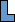 | 2 in 3×3
|  | 3 in 4×4
|  | 4 in 3×7 (GS)
| |
|---|
| |
Pentominoes
| Poly | Dist
|
|---|
 | 0 in 3×4
|  | 1 in 3×5
|  | 3 in 4×4
|  | 3 in 2×11
|  | 6 in 5×9
|  | 7 in 6×8
|  | 7 in 3×13 (GS)
| 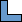 | 9 in 5×10
|  | 13 in 5×14 (BZ)
|  | 13 in 4×18 (BZ)
| |
|---|
| |
Hexominoes
| Poly | Dist
|
|---|
 | 0 in 3×5
|  | 1 in 2×3
|  | 2 in 4×7
|  | 3 in 2×14
|  | 4 in 3×15 (GS)
|  | 6 in 5×13 (GS)
|  | 7 in 6×11 (GS)
|  | 10 in 3×24 (GS)
| |
|---|
| |
Heptominoes
| Poly | Dist
|
|---|
 | 0 in 4×6
|  | 1 in 2×9
|  | 1 in 4×7 (GS)
|  | 2 in 5×8
|  | 3 in 2×11
|  | 5 in 6×6 (GS)
|  | 5 in 3×24 (GS)
|  | 6 in 23×3 (GS)
| 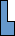 | 9 in 13×5 (GS)
| |
|---|
|
Here are the the known super-distinguishable polyominoes:
Small
Polyominoes
| Poly | Dist
|
|---|
 | 1 in 1×1
|  | 1 in 1×2
|  | 2 in 1×6
|  | 3 in 2×5
| |
|---|
| |
Tetrominoes
| Poly | Dist
|
|---|
 | 3 in 1×12
|  | 3 in 2×6
|  | 4 in 3×7 (GS)
|  | 7 in 4×8 (AB)
| 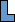 | 7 in 3×10 (AB)
| |
|---|
| |
Pentominoes
| Poly | Dist
|
|---|
 | 4 in 1×20
|  | 5 in 2×13
|  | 6 in 5×9
|  | 7 in 6×8
|  | 7 in 3×13 (GS)
| 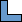 | 9 in 5×10
|  | 13 in 5×14 (BZ)
|  | 13 in 4×18 (BZ)
| |
|---|
|
Here are some distinguishable polyaboloes:
Small
Polyaboloes
| Poly | Dist
|
|---|
 | 0 in 0×0
|  | 1 in 1×1
| 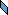 | 2 in 2×2
|  | 5 in 2×3 (GS)
| |
|---|
| |
Triaboloes
| Poly | Dist
|
|---|
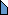 | 1 in 1×2
|  | 3 in 2×3
|  | 2 in 2×4 (GS)
|  | 3 in 2×4 (GS)
| |
|---|
| |
Tetraboloes
| Poly | Dist
|
|---|
 | 1 in 1×2
|  | 1 in 2×4 (GS)
|  | 5 in 3×5 (GS)
|  | 5 in 2×10 (GS)
|  | 5 in 2×9 (GS)
|  | 5 in 2×7 (GS)
|  | 11 in 3×8 (GS)
| |
|---|
|
Here are some distinguishable polykings:
Small
Polykings
| Poly | Dist
|
|---|
 | 0 in 0×0
| 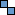 | 0 in 1×2
|  | 1 in 1×2
| |
|---|
| |
Trikings
| Poly | Dist
|
|---|
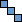 | 0 in 2×3
|  | 1 in 1×3
|  | 1 in 2×2 (GS)
| 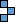 | 8 in 4×7 (GS)
| 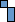 | none (BH)
| |
|---|
| |
Tetrakings
| Poly | Dist
|
|---|
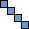 | 0 in 3×4 (GS)
|  | 1 in 1×4 (GS)
|  | 1 in 2×2 (GS)
| 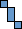 | 1 in 3×4 (GS)
| 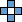 | 4 in 4×8 (GS)
| 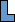 | 5 in 3×7 (GS)
| 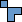 | 5 in 4×8 (GS)
| 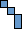 | 6 in 6×6 (GS)
| |
|---|
|
2.
If there is a k×k n-puzzle, then putting 2-piece rings around it can create a (k+2)×(k+2) 2n-puzzle, 4n-puzzle, or 8n-puzzle.
If there is a solution for n, David Wilson pointed out there is a solution for 3n by putting a copy of the n-puzzle inside a modified 3-puzzle due to George Sicherman.
There is a n×n 2n-puzzle comprised of (n–1) n×1 rectangles and n 1×1 squares.
There is a (4n+1)-puzzle comprised of a 2×2 square inside a totally symmetric field of 1×1 squares.
Here are the best-known solutions for a square tray:

1
| 
2
| 
3
(DW)
| 
4
| 
5
| 
6
| 
7
(GS)
| 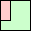
8
| 
9
| 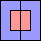
10
(GS)
|

11
(GS)
| 
12
| 
13
| 
14
(GS)
| 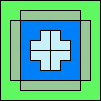
15
(DW)
| 
16
| 
17
| 
18
| 
19
(DW)
| 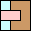
20
|

21
(GS)
| 
22
| 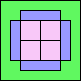
23
(GS)
| 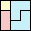
24
(GS)
| 
25
| 
26
| 
27
| 
28
(GS)
| 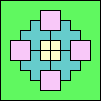
29
(GS)
| 
30
(GS)
|
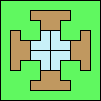
31
(DW)
| 
32
| 
33
| 
34
(GS)
| 
35
(DW)
| 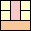
36
| 
37
| 
38
(GS)
| 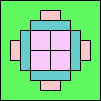
39
(GS)
| 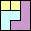
40
|

41
(GT)
| 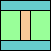
42
(GS)
| 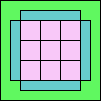
43
(GS)
| 
44
| 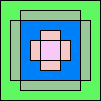
45
(BH)
| 
46
| 
47
(GS)
| 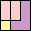
48
| 
49
| 
50
(GS)
|
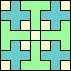
51
(GS)
| 
52
| 
53
| 
54
(GS)
| 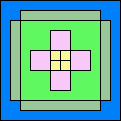
55
| 
56
| 
57
| 
58
(GS)
| 
59
(BH)
| 
60
|

61
| 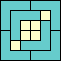
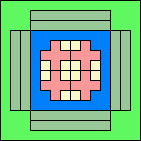
62
(GS)
| 
63
(GT)
| 
64
(GS)
| 
65
(GS)
| 
66
(GS)
| 
67
(GS)
| 
68
| 
69
| 
70
|
23×23
71
(DW)
| 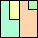
72
(PH)
| 
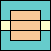
73
(GS)
| 
74
(GS)
| 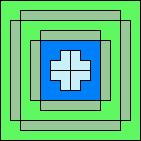
75
| 
76
(PH)
| 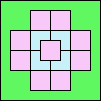
77
(GS)
| 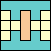
78
(GS)
| 
79
| 
80
|
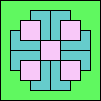
81
(GS)
| 
82
(GS)
| 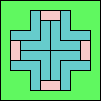
83
(GS)
| 
84
(GS)
| 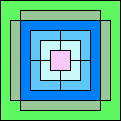
85
(DW)
| 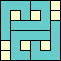
86
(GS)
| 20×20
87
(BH)
| 
88
(GS)
| 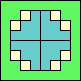
89
(GS)
| 
90
|
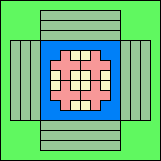
91
(GT)
| 
92
(GS)
| 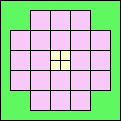
93
(GS)
| 
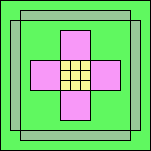
94
(GS)
| 
95
| 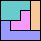
96
(GS)
| 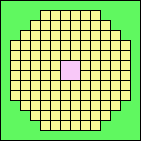
97
| 
98
(GS)
| 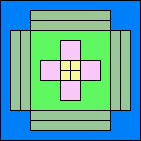
99
(DW)
| 
100
(GS)
|
There are always solutions for rectangles because there is a (n+1)×1 n-puzzle comprised of 1 domino and (n–1) single squares.
And here are the best-known solutions for a rectangular tray:

1
| 
2
| 
3
| 
4
| 
5
| 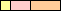
6
| 
7
| 
8
| 
9
(GS)
| 
10
|

11
| 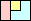
12
| 
13
| 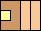
14
(PH)
| 
15
| 
16
| 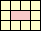
17
(GS)
| 
18
| 
19
(GS)
| 
20
(GS)
|

21
| 
22
| 
23
(PH)
| 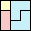
24
(GS)
| 
25
(GS)
| 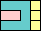
26
(PH)
| 
27
(GS)
| 
28
(GS)
| 
29
| 
30
|

31
(GS)
| 
32
(GS)
| 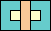
33
(GS)
| 
34
(GS)
| 
35
| 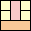
36
| 
37
(PH)
| 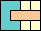
38
(GS)
| 
39
(PH)
| 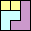
40
|

41
(PH)
| 
42
| 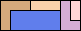
43
(PH)
| 
44
| 
45
| 
46
(GS)
| 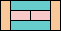
47
(GS)
| 
48
| 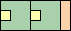
49
(PH)
| 
50
(GS)
|

51
(GS)
| 
52
| 
53
(PH)
| 
54
(GS)
| 
55
| 
56
| 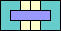
57
(GS)
| 
58
(GS)
| 
59
(PH)
| 
60
|

61
(GS)
| 
62
(GS)
| 
63
(PH)
| 
64
(GS)
| 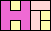
65
(PH)
| 
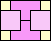
66
(GS)
| 
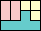
67
(GS)
| 
68
(GS)
| 
69
(GS)
| 
70
|

71
(GS)
| 
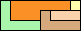
72
(GS)
| 
73
(PH)
| 
74
(GS)
| 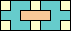
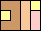
75
(GS)
| 
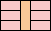
76
(PH)
| 
77
(GS)
| 
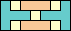
78
(GS)
| 
79
(GS)
| 
80
|
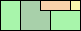
81
(PH)
| 
82
(GS)
| 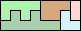
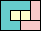
83
(PH)
| 
84
(GS)
| 
85
(PH)
| 
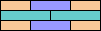
86
(GS)
| 
87
(GS)
| 
88
(GS)
| 
89
| 
90
(GS)
|

91
| 
92
(GS)
| 
93
(PH)
| 
94
| 
95
(GS)
| 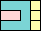
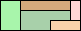
96
(PH)
| 
97
(PH)
| 
98
(GS)
| 
99
(PH)
| 
100
(GS)
|
If you can extend any of these results, please
e-mail me.
Click here to go back to Math Magic. Last updated 8/20/11.