




5




4







8
 (BZ)
(BZ)


12
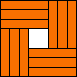


 (GS)
(GS)



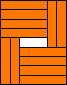
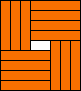 (GS)
(GS)




8



 (BZ)
(BZ)


 (GS)
(GS)
 (GS)
(GS)

 (BZ)
(BZ)
 (BZ)
(BZ)
 (BZ)
(BZ)
| n \ m | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | none | none | 3 
5
| none
| 3 | 
4 | 
4 |   5 
6
| none
| 3 | 
none
| 5 | 
none
| 7
| none
| none
| 3 |  4  
4 | 
none
| 6 | 
8
| none
| none
| 6 | 
6 | 
6 |  8  (BZ) (BZ)
7 | 
11 |  12  
  (GS) (GS)
9
| none
| 3 | 
4 | 
none
| 10 | 
12 | 
14 |  (GS) (GS)
10
| 4 | 
6 | 
6 |   8 
6 | 
8 | 
none
| 15 |  (BZ) (BZ)
11
| 4 |  
none
| 5 |  (GS) (GS)
none
| 12 |  (GS) (GS)
none
| none
| 12
| none
| 4 | 
none
| none
| 13 |  (BZ) (BZ)
16 |  (BZ) (BZ)
18 |  (BZ) (BZ)
|
| n \ m | 9 | 10 | 11 | 12 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9 | 16 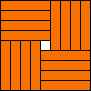 (GS) (GS)
10
| 17 |  (BZ) (BZ)
none
| 11
| none
| 19 |  (BZ) (BZ)
21 |  (BZ) (BZ)
12
| 18 |  (BZ) (BZ)
17 |  (BZ) (BZ)
none
| 27 |  (BZ) (BZ)28  (BZ) (BZ)
|
| n \ m | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | none | none | 3   (GS) (GS)
| 3   4   
6
| none
| 3 |  
3 |  4   
4 |     5  
4 |   5  6  
7
| none
| 3 | 
3 |  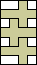  4 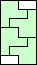 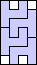 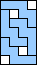
4 |  
5 | 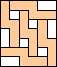 6 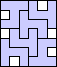
6 | 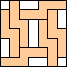 8 
8
| none
| 3 | 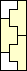     4 
none
| 6 |  
6 | 
none
| 8 |    10  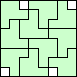 (all GS) (all GS)
9
| 3 | 
3 | 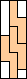  4 
4 |   5  6 
none
| 8 | 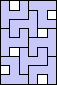
10 | 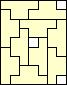
9 |  (GS) (GS)11 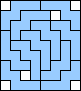 (BZ) (BZ)
10
| 3 |  
4 | 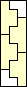  5 
5 |  6   
6 |  
8 | 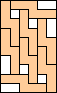 9 
10 |  (BZ) (BZ)11  (BZ) (BZ)
none
| 11
| 3 |  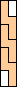
4 |    5 
5 |   6 
none
| 8 |  (GS) (GS)9  (GS) (GS)10  (GS) (GS)
none
| 14 | 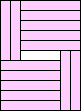  (all BZ) (all BZ)
12
| 4 |  
5 | 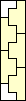    (GS) (GS)6  
7 |  8  
10 |   (all GS) (all GS)
10 | 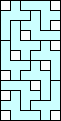 (GS) (GS)11  (GS) (GS)
none
| none
| |
| n \ m | 9 | 10 | 11 | 12 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9 | 11 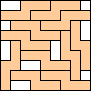 (BZ) (BZ)12  (BZ) (BZ)
10
| 11 | 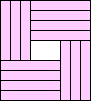 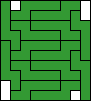 (all BZ) (all BZ)
14 | 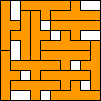 (BZ) (BZ)16  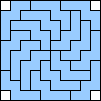
11
| 16 | 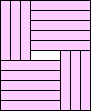 (BZ) (BZ)
16 | 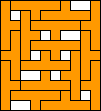 (BZ) (BZ)17  (BZ) (BZ)18 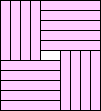  (BZ) (BZ)
16 |  (BZ) (BZ)17 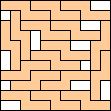 (BZ) (BZ)20  (BZ) (BZ)
12
| 16 | 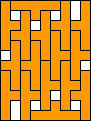 (BZ) (BZ)18  (BZ) (BZ)
16 |   (BZ) (BZ)
none
| 20 |   (all BZ) (all BZ)
|
| n \ m | 3 | 4 | 5 | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | none | none | 3  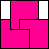 
6
| none
| 3 |  
3 |   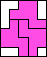     4    
7
| 3 | 
3 | 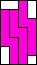    
4 
3 |   4      
5 
8
| none
| 3 |     4 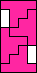 
3 |  4    5 
9
| 3 |    
3 |  4     
4 |   5    6  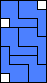
10
| 3 |    
4 |   5 
4 |  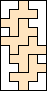 5  6    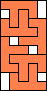 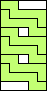  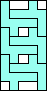 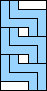
11
| 3 |     4   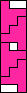   
3 |  4   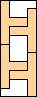 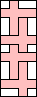 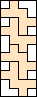 5    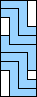 6 
5 |   6   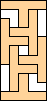 7 
12
| 3 |  4 
4 | 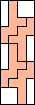 5 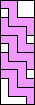 6  
6 |  (GS) (GS)8  (GS) (GS)
|
| n \ m | 6 | 7 | 8 | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 3   4    
7
| 4 | 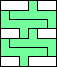 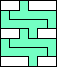 
5 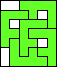 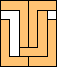  6 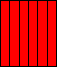
5 | 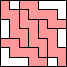 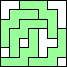 6  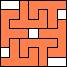 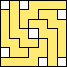 7 
8
| 4 |  6 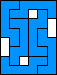   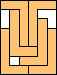
6 |  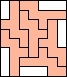
7  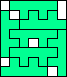
7 |  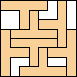  8  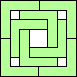   
9
| 6 | 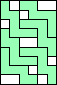 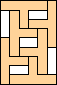
7 | 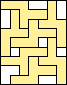 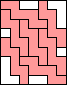 8  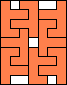 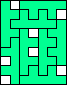
8 | 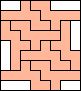   (all GS) (all GS)9 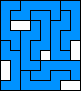 (GS) (GS)10  (GS) (GS)
10
| 6 | 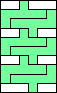 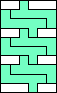    7   8    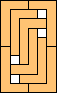
6 | 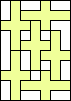 (GS) (GS)7  (GS) (GS)8 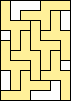  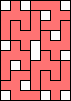 (all GS) (all GS)9  (GS) (GS)
8 |  (GS) (GS)9  (GS) (GS)10 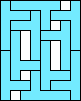 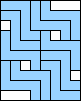  (all GS) (all GS)
11
| 6 |  (GS) (GS)8 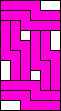  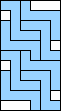
8 | 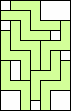 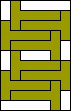 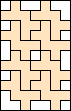 (all GS) (all GS)9 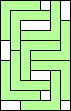  (all GS) (all GS)
9 | 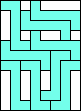 (GS) (GS)10 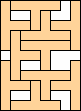  (all GS) (all GS)
12
| 9 | 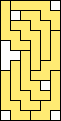 (GS) (GS)10  (GS) (GS)
8 | 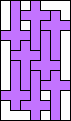 (GS) (GS)10 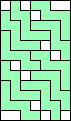 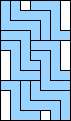 (all GS) (all GS)
12 | 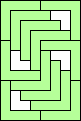 (GS) (GS)
|
| Pentominoes | 3 
| 
| 5 
| 6 
| 7 
| 11 
| 13 
|
15 
| 17 
| 
| 21 
| 27 
|
| Hexominoes | 3 
| 
| 
| 
| 
| 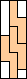
| 
| 5 
| 
| 
| 6 
| 7 
| 9 
| 
| 
|
10 
| 11 
| 
| 
| 14 
| 16 
| 17 
|
| Heptominoes | 3 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
4 
| 
| 
| 5 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
6 
| 
| 
| 
| 7 
| 
| 
| 
| 
| 
| 
| 
|

| 
| 8 
| 
| 9 
| 
| 
| 
| 
| 
| 
| 10 
|
Berend van der Zwaag proved that the P-hexomino only packs the 5×5 rectangle uniquely, essentially by showing that large rectangles can always be packed with fewer than 6 unused squares, and that parts of the packing can be rotated.
George Sicherman also found unique solutions of packing polyominoes in cylinders:
| n \ m | 3 | 4 | 5 | 6 | 7 | 8 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | none | none | none | none | none | 4 
4
| none
| none
| 3 | 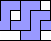
4 | 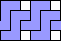 
none
| 4 |  6 
5
| 3 | 
4 | 
none
| 4 | 
none
| none
| |
| n \ m | 3 | 4 | 5 | 6 | 7 | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | none | none | none | 3    
| 3 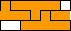  
4
| none
| none
| 3 | 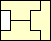   
4 |     
none
| 5
| none
| 3 |  
3 |   4      
4 | 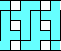 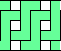 5 
none
| 6
| 3 | 
3 |   4   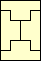
5 |  
none
| 6 | 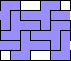 7 
7
| none
| 4 | 
none
| none
| 8 | 
|
| n \ m | 3 | 4 | 5 | 6 | 7 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | none | none | none | 3   
| none | ||||||||||||
| 5 | none | none | none | 3  4 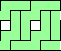 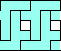 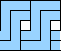
| 4 
6
| none
| 3 | 
none
| none
| 4 |     
7
| 3 |  
none
| 4 | 
4 | 
none
| |
George Sicherman also found unique solutions of packing polyominoes in triangles:



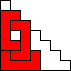
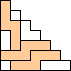
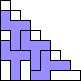
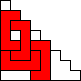
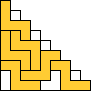
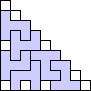
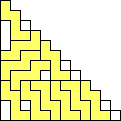 (BZ)
(BZ)  (BZ)
(BZ)  (BZ)
(BZ)
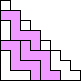
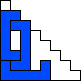
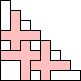



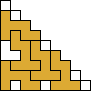
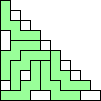
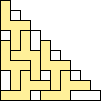
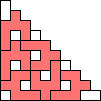
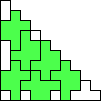
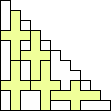
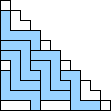
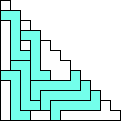
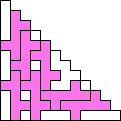
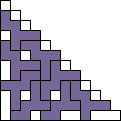
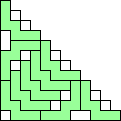
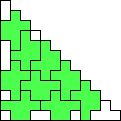
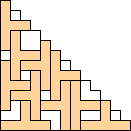
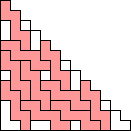
George Sicherman also found unique solutions of packing polyominoes in pyramids:
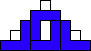
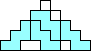
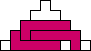
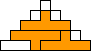
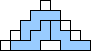
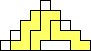
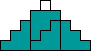
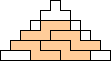
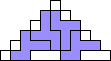
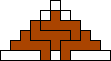
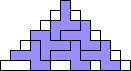
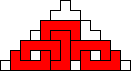
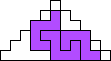

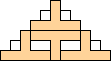
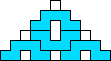
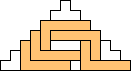
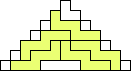
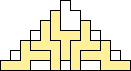
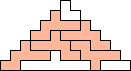
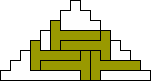
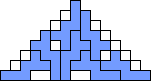
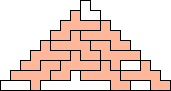
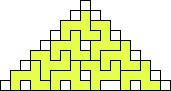
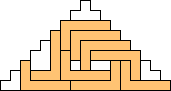
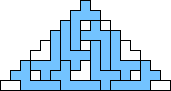
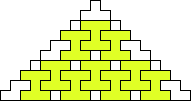
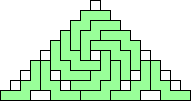
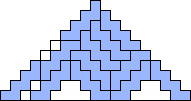
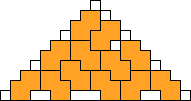
George Sicherman also found unique solutions of packing polyominoes in diamonds:

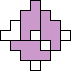
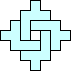



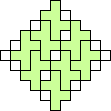
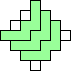
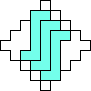
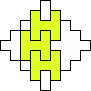
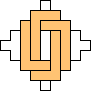
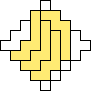
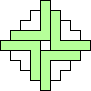
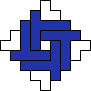
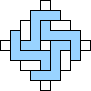
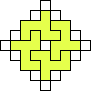
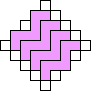
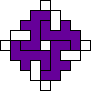
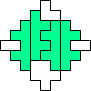
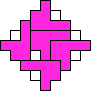

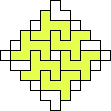
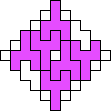
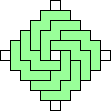
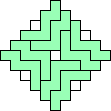
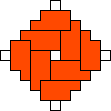

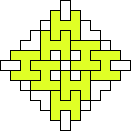
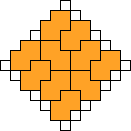
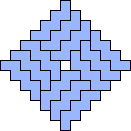
George Sicherman also found unique solutions of packing polyiamonds in triangles:
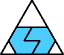




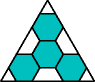





















If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 9/26/09.