Problem of the Month (September 2014)

Consider the sided-polyominoes below representing the digits 0-8:

We say two sets of polyominoes X and Y are equal if they both tile the same shape. For example, 3+3 = 1+1+1+7 because of the following tilings:

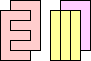
We say two sets of polyominoes X and Y are equivalent if there is another set of polyominoes Z so that X and Z tile the same shape as Y and Z. For example, 3 ≈ 5 because of the following tilings:

What sets of digits are equal? What sets of digits are equivalent? If X ≈ Y, what is the smallest area Z with X + Z = Y + Z? Are every set of polyominoes with equal area equivalent?

ANSWERS

Bryce Herdt proved that all sets of numerical polyominoes of equal area are equivalent. His proof: Cancel the 0's with 0 ≈ 17, the 6's with 46 ≈ 113, and the 8's with 18 ≈ 37. The 2's, 3's, and 5's can drop out with 1x ≈ 47, and the 4's go with 14 ≈ 77. Only 1's and 7's may be left, and these will be in a 7:5 ratio.

Smallest Known Equivalencies
AreaEquivalencyAddTiling
112 ≈ 31+7
2 ≈ 51+1+7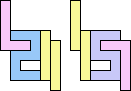
(George Sicherman)
3 ≈ 51+7
120 ≈ 61+4+7+7
(George Sicherman)
0 ≈ 1+71+7
6 ≈ 1+71+3+7
(George Sicherman)
141+4 ≈ 7+71
161+2 ≈ 4+71+7
1+3 ≈ 4+77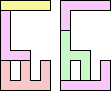
(Bryce Herdt)
1+5 ≈ 4+71+7
(George Sicherman)
181+8 ≈ 2+71+1+1+4+7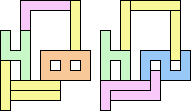
(George Sicherman)
1+8 ≈ 3+71+6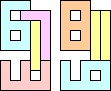
1+8 ≈ 4+41+1+1+6+7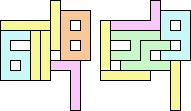
(George Sicherman)
1+8 ≈ 5+71+6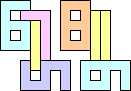
2+7 ≈ 4+41+1+1+7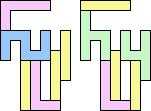
(George Sicherman)
3+7 ≈ 4+41+7
(George Sicherman)
4+4 ≈ 5+71+1+1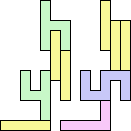
(George Sicherman)
190+7 ≈ 1+1+41+1+7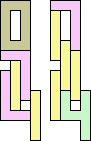
(George Sicherman)
6+7 ≈ 1+1+41+7
(George Sicherman)
202+4 ≈ 7+81+1+1+1+3+6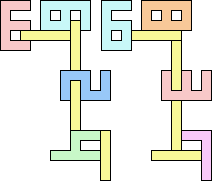
(Bryce Herdt)
2+4 ≈ 1+1+1+17+7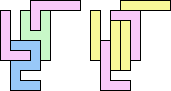
(George Sicherman)
3+4 ≈ 7+81+1+6
(George Sicherman)
3+4 ≈ 1+1+1+17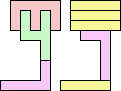
(George Sicherman)
4+5 ≈ 7+81+1+6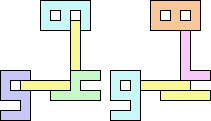
(Bryce Herdt)
4+5 ≈ 1+1+1+17+7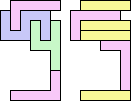
(George Sicherman)
7+8 ≈ 1+1+1+11+1+3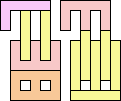
(George Sicherman)
210+4 ≈ 1+1+21+3+7+7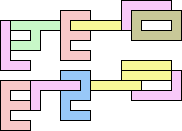
(Bryce Herdt)
0+4 ≈ 1+1+37+7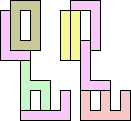
(Bryce Herdt)
0+4 ≈ 1+1+51+7+7
(George Sicherman)
0+4 ≈ 7+7+71+1
4+6 ≈ 1+1+21+1+1+7
(George Sicherman)
4+6 ≈ 1+1+31+7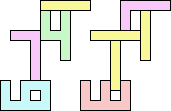
(George Sicherman)
4+6 ≈ 1+1+51+7
(Bryce Herdt)
4+6 ≈ 7+7+71+1+1+7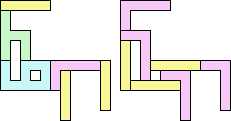
(George Sicherman)
1+1+2 ≈ 7+7+71+7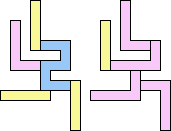
1+1+3 ≈ 7+7+71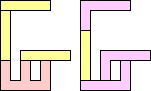
1+1+5 ≈ 7+7+73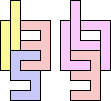
(George Sicherman)
222+2 ≈ 3+31+1+7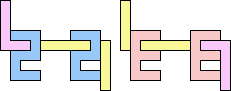
(Bryce Herdt)
2+2 ≈ 3+51+1+1+7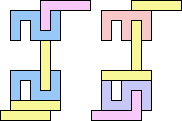
(Bryce Herdt)
2+2 ≈ 4+81+1+3+6+7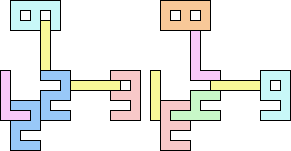
(Bryce Herdt)
2+2 ≈ 5+51+1+1+1+7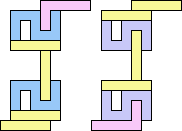
(Bryce Herdt)
2+2 ≈ 0+1+11+1+1+7+7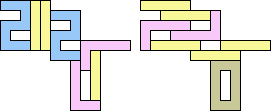
(Bryce Herdt)
2+2 ≈ 1+1+61+1+1+3+7
(Bryce Herdt)
2+2 ≈ 1+1+1+71+1+7
(George Sicherman)
2+3 ≈ 4+81+1+6+7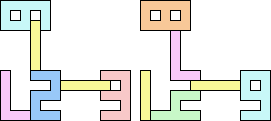
(Bryce Herdt)
2+3 ≈ 5+51+1+1+7
(Bryce Herdt)
2+3 ≈ 0+1+11+1+1+7+7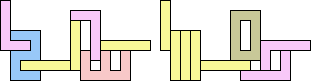
(Bryce Herdt)
2+3 ≈ 1+1+61+1+7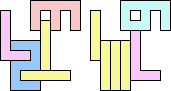
(George Sicherman)
2+3 ≈ 1+1+1+71+1+7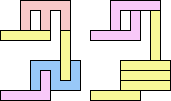
(George Sicherman)
2+5 ≈ 3+31+1+7
(Bryce Herdt)
2+5 ≈ 4+81+1+6+7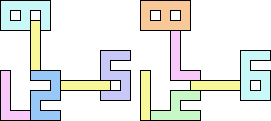
(Bryce Herdt)
2+5 ≈ 0+1+11+1+1+7+7+7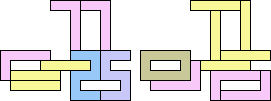
(Bryce Herdt)
2+5 ≈ 1+1+61+1+7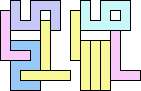
(George Sicherman)
2+5 ≈ 1+1+1+71+1+7+7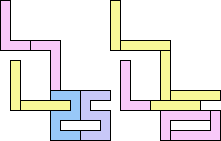
(George Sicherman)
3+3 ≈ 4+81+1+6+7
(Bryce Herdt)
3+3 ≈ 5+51+1+7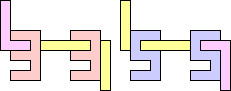
(Bryce Herdt)
3+3 ≈ 0+1+11+7+7
(George Sicherman)
3+3 ≈ 1+1+61+1+7
(George Sicherman)
3+3 = 1+1+1+7-
3+5 ≈ 4+81+1+6+7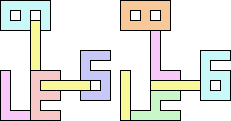
(Bryce Herdt)
3+5 ≈ 0+1+11+1+1+7+7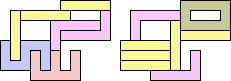
(George Sicherman)
3+5 ≈ 1+1+61+1+7
(George Sicherman)
3+5 ≈ 1+1+1+77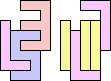
(George Sicherman)
4+8 ≈ 5+51+1+6+7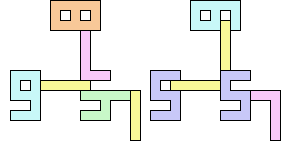
(Bryce Herdt)
4+8 ≈ 0+1+11+1+1+1+3+7+7
(George Sicherman)
4+8 ≈ 1+1+61+7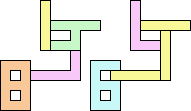
(George Sicherman)
4+8 ≈ 1+1+1+71+1+3
(George Sicherman)
5+5 ≈ 0+1+11+1+1+7+7+7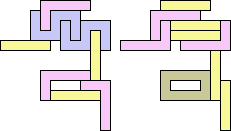
(Bryce Herdt)
5+5 ≈ 1+1+61+1+7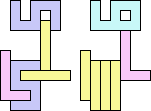
(George Sicherman)
5+5 ≈ 1+1+1+71+7+7

Smallest Known Tilings Showing An = Bm
EquationTiling
122 = 310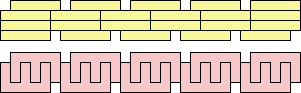
(George Sicherman)
136 = 420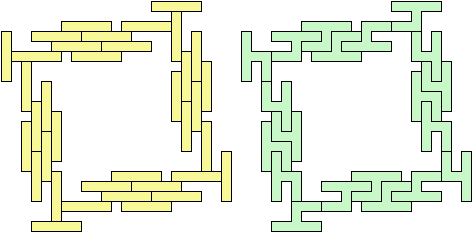
(George Sicherman)
17 = 75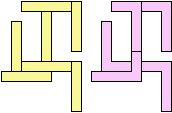
(George Sicherman)

Smallest Known Tilings
Showing An = Bm Cp
EquationTiling
02 = 12 72
118 = 02 36
(George Sicherman)
112 = 02 44
(George Sicherman)
18 = 0 74
(Maurizio Morandi)
122 = 22 38
(George Sicherman)
15 = 2 72
18 = 32 42
(George Sicherman)
122 = 38 52
(George Sicherman)
110 = 32 74
(Maurizio Morandi)
129 = 312 8
(George Sicherman)
18 = 42 52
(George Sicherman)
16 = 4 73
(Bryce Herdt)
15 = 5 72
18 = 6 74
(George Sicherman)
18 = 72 82
(George Sicherman)
322 = 142 22
(George Sicherman)
EquationTiling
36 = 16 44
(George Sicherman)
322 = 142 52
(George Sicherman)
314 = 126 62
(George Sicherman)
32 = 13 7
316 = 130 82
(Bryce Herdt)
316 = 44 720
(George Sicherman)
46 = 18 72
(George Sicherman)
62 = 12 72
76 = 0 16
(George Sicherman)
76 = 14 22
(Maurizio Morandi)
76 = 14 32
(Maurizio Morandi)
74 = 12 42
76 = 14 52
(George Sicherman)
76 = 16 6
(George Sicherman)
78 = 16 82
(George Sicherman)
710 = 34 82
(George Sicherman)

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 9/20/14.