
s = 0
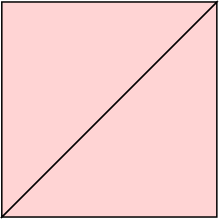
s = 1
k=1 s = 0 | k=2 s = 1 |
k=4 s = 0 | k=5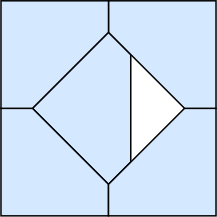 s = 1/√2 = .707+ | k=6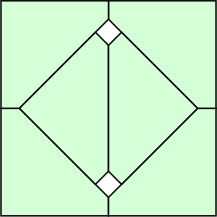 s = 2√2–2 = .828+ | k=8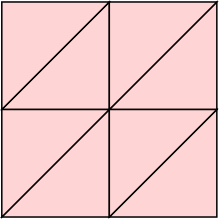 s = 1 |
k=9 s = 0 | k=10 s = (15√2–4)/28 = .614+ Maurizio Morandi | k=11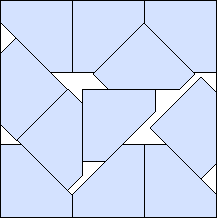 s = (24√2–18)/23 = .693+ Maurizio Morandi | k=12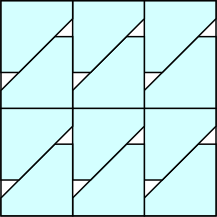 s = 3/4 = .750 |
k=13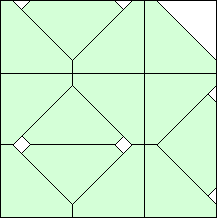 s = 2√2–2 = .828+ Maurizio Morandi | k=14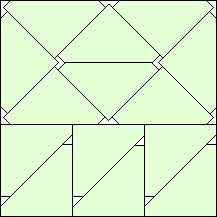 s = (19–11√2)/4 = .860+ Maurizio Morandi | k=15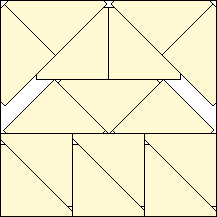 s = (11√2–10)/6 = .926+ Maurizio Morandi | k=16 s = (8–3√2)/4 = .939+ |
k=18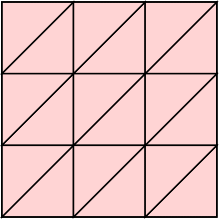 s = 1 |
k=16 s = 0 | k=17 s = (33√2–28)/34 = .549+ Maurizio Morandi | k=18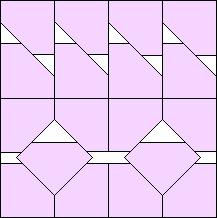 s = (1+√2)/4 = .603+ Maurizio Morandi | k=19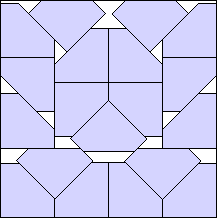 s = (73√2–44)/89 = .665+ Maurizio Morandi |
k=20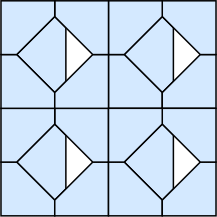 s = 1/√2 = .707+ | k=21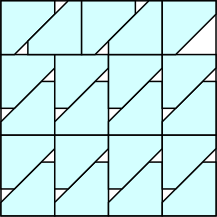 s = 3/4 = .750 | k=22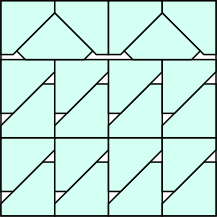 s = (4+√2)/7 = .773+ | k=24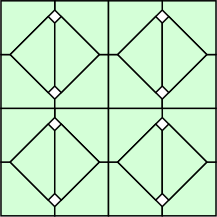 s = 2√2–2 = .828+ |
k=26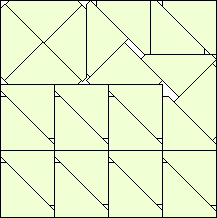 s = (24√2–9)/28 = .890+ Maurizio Morandi | k=28 s = (17+79√2)/137 = .939+ Maurizio Morandi | k=30 s = (90√2–105)/23 = .968+ Maurizio Morandi | k=32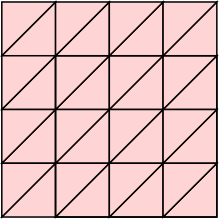 s = 1 |
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 9/19/17.