Shapes that can be tiled with smaller copies of themselves, not necessarily all the same size, are called irreptiles. Whereas reptiles have been well-studied, irreptiles have not. Here are a few to whet your appetite:

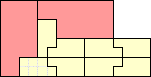What irreptiles can you find? For a given shape, we call its order the smallest number of copies needed to tile it. What are the orders of some irreptiles? Can you find a shape with order 2? Are there irreptiles with arbitrarily large orders? Are there irreptiles with all possible orders? Can you find a polyomino irreptile that cannot tile any rectangles?

Stewart Hinsley is an expert in fractile reptiles. See his page here.

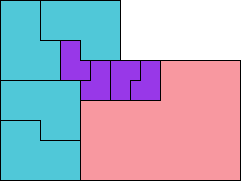
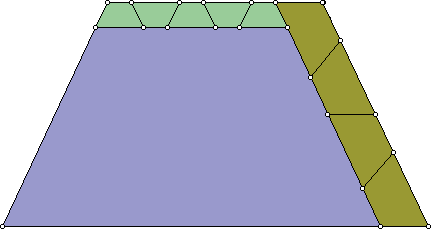
Andrew Bayly found that right triangles have order 2, and all other triangles have order 4. He also found 2 of the 3 rectangles with order 3, and that all other rectangles have order 4. He came up with a sequence of trapezoids which he thought might have all large orders, but he didn't know how to prove this.

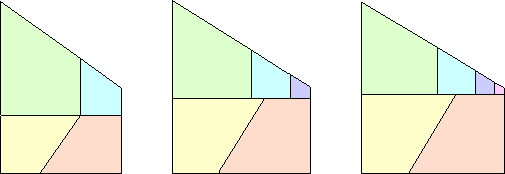
Stewart Hinsley gave a similar construction but couldn't prove that these trapezoids didn't have a smaller order. He did eventually prove that there are trapezoids of all odd orders. Here is his trapezoid of order 5:

Stewart Hinsley also says he can prove that there are rectangular reptiles corresponding to all unit quadratic Pisot numbers.

Andrew Bayly also came up with a sequence of polyomino examples to show that arbitrarily large orders exist. If we take a polyomino where 2 of them tile a square, and one of them has a very thin part, it takes a lot of copies to tile the thin part.

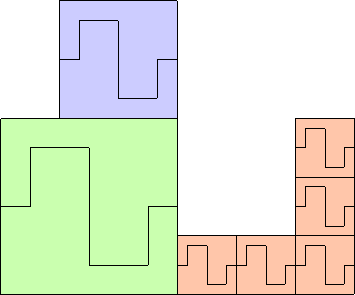
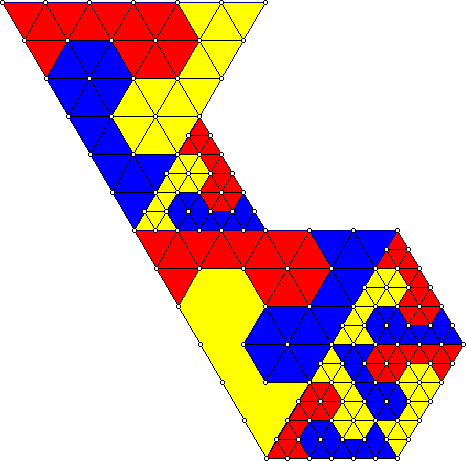
Both Andrew Bayly and Jeremy Galvagni found polyiamond examples of irreptiles using the same ideas:

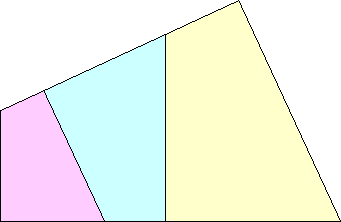
Mike Reid found an infinite family of cyclic quadrilaterals with order 3:

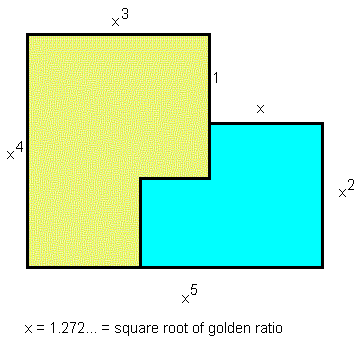
Karl Scherer found a polygonal reptile with order 2, which he calls the "golden bee":

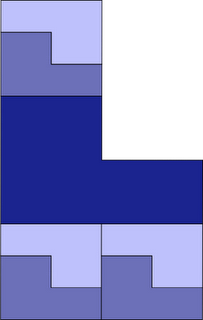
Ernesto Amezcua found these three L-shaped reptiles of order 7. The left one has height/width ratio of √3, the center one has height/width ratio of √(5/2), and the right one has height/width ratio of √(5/3).

Shape Smallest Irreptile Packing Source 4 Trivial 4 Trivial 4 Trivial 16 Karl Scherer 4 Trivial 10 Karl Scherer 40 Karl Scherer 8 Karl Scherer 9 Mike Reid 12 Rodolfo Kurchan 18 Rodolfo Kurchan 22 Mike Reid 30 George Sicherman 63 Livio Zucca 10 Karl Scherer 14 George Sicherman 68 Mike Reid 10 Mike Reid 10 Karl Scherer

Shape Smallest Irreptile Packing Source 10 George Sicherman 10 George Sicherman 10 George Sicherman 10 Karl Scherer 40 Mike Reid 34 George Sicherman 12 Erich Friedman 12 Erich Friedman 12 Erich Friedman 12 Erich Friedman 12 Erich Friedman 12 Erich Friedman 14 George Sicherman 17 Mike Reid 9 George Sicherman 7 Mike Reid 62 Mike Reid

Polyaboloes Shape Smallest Irreptile Packing Source 3 Karl Scherer 8 George Sicherman 34 George Sicherman 8 Karl Scherer 5 Karl Scherer 14 George Sicherman 34 Karl Scherer 17 George Sicherman 8 Karl Scherer 16 George Sicherman 5 George Sicherman 16 George Sicherman 5 George Sicherman 8 George Sicherman

Polyiamonds Shape Smallest Irreptile Packing Source 10 George Sicherman 6 Karl Scherer 6 Karl Scherer 16 Karl Scherer 14 George Sicherman 10 Karl Scherer 10 Karl Scherer 20 George Sicherman 14 Karl Scherer 10 George Sicherman 5 Karl Scherer 55 Andrew Bayly

Polydrafters Shape Smallest Irreptile Packing Source 2 George Sicherman 5 Karl Scherer 8 George Sicherman 8 George Sicherman 17 George Sicherman 35 George Sicherman 6 George Sicherman 10 George Sicherman 6 Karl Scherer 7 George Sicherman 12 George Sicherman 10 George Sicherman

Polydoms Shape Smallest Irreptile Packing Source 2 George Sicherman 6 Karl Scherer 8 George Sicherman 9 George Sicherman 9 Karl Scherer 10 Bryce Herdt 14 Bryce Herdt 6 George Sicherman 6 George Sicherman 17 George Sicherman 16 George Sicherman 6 George Sicherman 6 George Sicherman 6 George Sicherman 6 George Sicherman 6 George Sicherman 6 George Sicherman 9 George Sicherman 13 George Sicherman 10 George Sicherman 8 Karl Scherer

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 10/10/18.