



3/8 (GS)

1/3 (GS)

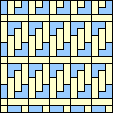
1/3 (GS)

1/3 (GS)
1.
Pick polyominoes B (shown in Blue) and Y (shown in Yellow). If we tile the plane with copies of B and Y, what is the largest density that copies of B can have in the plane if the copies don't touch, even at the corners? (In other words, how sparsely can we pack the plane with copies of Y so that the holes don't touch and are congruent to B?)
2.
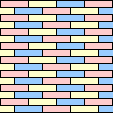
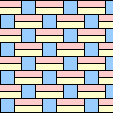
Pick polyominoes B (shown in Blue), Y (shown in Yellow), and R (shown in Red). Can we tile the plane with B, Y, and R so that no tile touches another of the same color? (In other words, is there a 3-color tiling of the plane with these tiles?)
1.
Here are the best known results:
 | 
| |
|---|---|---|

|  3/8 (GS) |  1/3 (GS) |

|  1/3 (GS) |  1/3 (GS) |
 | 
| |
|---|---|---|

|  2/5 (GS) |  4/13 (GS) |

| 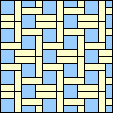 2/5 (GS) |  2/5 (GS) |

|  2/5 (GS) |  2/5 (GS) |

|  2/5 (GS) |  2/5 (GS) |

|  1/3 (GS) |  2/5 (GS) |
 |  |  |  | 
| |
|---|---|---|---|---|---|

|  3/8 (GS) |  3/11 (GS) |  1/3 (GS) |  1/3 (GS) |  3/11 (GS) |

|  1/3 (GS) |  3/14 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |
 |  |  |  | 
| |
|---|---|---|---|---|---|

| 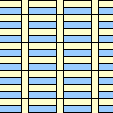 2/5 | 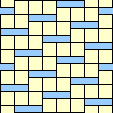 1/4 |  2/5 |  1/3 |  1/3 |

| 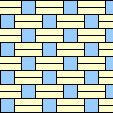 1/3 (GS) | 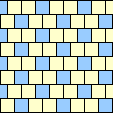 1/3 (GS) |  2/5 | 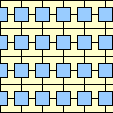 1/3 |  1/3 |

|  1/3 (GS) | 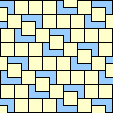 2/7 |  2/5 |  1/3 |  1/3 |

| 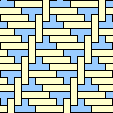 1/3 |  0 |  2/5 (GS) |  1/3 |  1/3 |

|  1/3 |  1/3 |  2/5 |  1/3 |  3/8 (GS) |
 |  |  |  |  | 
| |
|---|---|---|---|---|---|---|

| 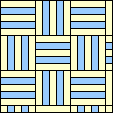 2/5 (GS) | 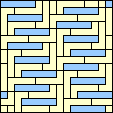 1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) | 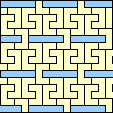 1/6 (GS) |

|  1/3 (GS) |  3/8 (GS) |  2/5 (GS) |  3/8 (GS) | 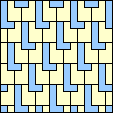 1/3 (GS) |  1/4 (GS) |

|  1/4 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) | 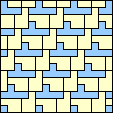 1/3 (GS) |  1/3 (GS) |

|  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  3/8 (GS) |  1/3 (GS) |  1/4 (GS) |

| 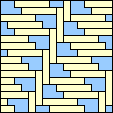 1/3 (GS) |  4/9 (GS) |  2/5 (GS) |  4/9 (GS) |  2/5 (GS) |  1/3 (GS) |

|  1/4 (GS) |  1/3 (GS) |  5/14 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |

| 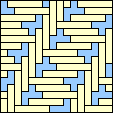 1/4 (GS) |  1/3 (GS) |  1/3 (GS) |  3/8 (GS) |  1/3 (GS) |  1/3 (GS) |

|  2/7 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/4 (GS) |

|  1/3 (GS) |  3/8 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/6 (GS) |

|  1/5 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/4 (GS) |

|  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |

|  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/4 (GS) |
 |  |  |  |  | 
| |
|---|---|---|---|---|---|---|

|  1/4 (GS) |  1/4 (GS) |  1/3 (GS) |  1/6 (GS) |  0 (GS) |  1/4 (GS) |

|  2/7 (GS) |  1/3 (GS) |  2/5 (GS) |  1/4 (GS) |  0 (GS) |  1/3 (GS) |

|  1/3 (GS) |  1/3 (GS) |  1/4 (GS) |  1/4 (GS) |  0 (GS) |  1/3 (GS) |

|  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  0 (GS) |  1/3 (GS) |

|  5/12 (GS) |  3/8 (GS) |  5/13 (GS) |  1/3 (GS) |  1/3 (GS) |  3/8 (GS) |

|  3/8 (GS) |  5/16 (GS) |  3/10 (GS) |  2/7 (GS) |  1/4 (GS) |  1/3 (GS) |

|  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/3 (GS) |  1/4 (GS) |  2/5 (GS) |

|  1/3 (GS) |  1/3 (GS) |  1/4 (GS) |  1/4 (GS) |  0 (GS) |  1/3 (GS) |

|  1/4 (GS) |  1/4 (GS) |  1/3 (GS) |  1/4 (GS) |  0 (GS) |  1/3 (GS) |

|  1/3 (GS) |  1/3 (GS) |  1/5 (GS) |  1/3 (GS) |  0 (GS) |  2/7 (GS) |

|  1/3 (GS) |  1/3 (GS) |  1/6 (GS) |  1/3 (GS) |  1/4 (GS) |  1/4 (GS) |

|  1/3 (GS) |  1/3 (GS) |  5/13 (GS) |  2/7 (GS) |  1/4 (GS) |  1/3 (GS) |
 |  | 
| |
|---|---|---|---|

|  2/5 (GS) |  1/3 (GS) |  3/8 (GS) |

|  2/5 (GS) |  1/3 (GS) |  4/9 (GS) |
|  1/3 (GS) |  1/3 (GS) |  2/5 (GS) |
2.
Here are the known results.
 (GS) |  (GS) |  (GS) |  (GS) |
  |   |   |   |  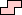
| |
|---|---|---|---|---|---|

| 
| none |  (JG) |  (JT) | 
|

| 
| 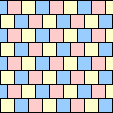
|  (GS) | 
| 
|

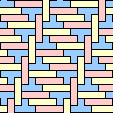
|  (JG) | none | 
|  (GS) |  (GS) |

| 
| none |  (GS) | 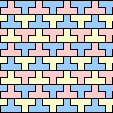
| none (PH) |

| 
| 
|  (GS) |  (GS) | 
|
 (JT) |  (GS) |  (GS) |    none (PH) |    none (JG) |
   none (JG) |  (GS) |    none (PH) |  (GS) |  (GS) |
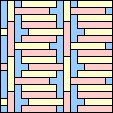
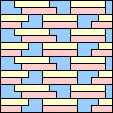
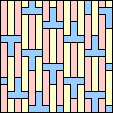
Jeremy Galvagni noted that if the polyominoes didn't have to be on the grid, that there is an additional solution:
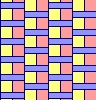
  |   |   |  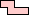 |   |  
| |
|---|---|---|---|---|---|---|

|  (GS) |  (GS) | none (GS) |  (GS) |  (GS) | none (GS) |

|  (GS) |  (GS) |  (GS) |  (GS) |  (GS) |  (GS) |

|  (GS) |  (GS) |  (GS) |  (GS) |  (GS) |  (GS) |

|  (GS) |  (GS) |  (GS) |  (GS) |  (GS) |  (GS) |

|  (GS) |  (GS) |  (GS) |  (GS) |  (GS) |  (JT) |

| none (GS) |  (GS) |  (GS) |  (GS) |  (GS) |  (GS) |

| none (GS) |  (GS) |  (GS) |  (GS) |  (GS) |  (GS) |

|  (PH) |  (GS) |  (GS) |  (PH) |  (GS) | none (GS) |

|  (GS) |  (GS) |  (GS) |  (GS) |  (GS) | none (JT) |

|  (GS) |  (GS) |  (PH) |  (GS) |  (GS) |  (PH) |

| none (GS) |  (GS) |  (GS) |  (GS) |  (GS) |  (GS) |

|  (GS) |  (GS) |  (GS) |  (GS) |  (GS) | none (GS) |
  |   |  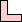 |   |   |  
| |
|---|---|---|---|---|---|---|

| none (GS) |  (PH) |  (GS) | none (GS) | none (GS) | none (GS) |

|  (GS) |  (PH) |  (GS) | none (GS) | none (GS) |  (PH) |

|  (GS) |  (GS) |  (GS) |  (PH) | none (GS) | none (GS) |

|  (GS) |  (PH) |  (GS) |  (AB) | none (GS) |  (PH) |

|  (GS) |  (GS) |  (GS) |  (GS) | none (GS) | none (GS) |

|  (GS) |  (GS) |  (GS) |  (GS) | none (GS) |  (PH) |

|  (GS) |  (GS) |  (GS) |  (GS) | none (GS) |  (GS) |

|  (GS) |  (GS) | none (GS) | none (GS) | none (GS) | none (GS) |

| none (GS) | none (GS) |  (GS) |  (AB) | none (PH) |  (PH) |

|  (GS) | none (GS) | none (GS) |  (GS) | none (GS) |  (GS) |

| none (GS) |  (GS) | none (GS) | none (GS) | none |  (GS) |

|  (GS) | none (GS) |  (GS) |  (PH) | none (PH) |  (GS) |
   ? |  (GS) |  (GS) |  (GS) |    none (GS) |
   none (GS) |  (PH) |  (PH) |    none (PH) |    none (PH) |
  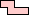 none (GS) |    none (PH) |    none (PH) |  (PH) |  (PH) |
  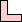 none (PH) |    none (PH) |    none (PH) |    none (PH) |  (GS) |
   none (PH) |  (PH) |    none (PH) |  (PH) |    none (PH) |
   none (PH) |    none (PH) |    none (PH) |  (PH) |  (PH) |
  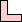 none (PH) |    none (PH) |    none (PH) |    none (PH) |    none (PH) |
   none (PH) |   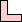 none (PH) |    none (PH) |    none (PH) |    none (PH) |
   none (PH) |   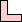 none (PH) |    none (PH) |    none (PH) |    none (PH) |
  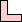 none (PH) |    none (PH) |    none (PH) |    none (PH) |    none (PH) |
   none (PH) |    none (PH) |    none (PH) |    none (PH) |    none (PH) |
 (GS) |  (GS) |    ? |  (GS) |  (GS) |
 (GS) |  (PH) |    none (PH) |  (PH) |  (GS) |
 (PH) |  (GS) |  (GS) |  (GS) |  (GS) |
   none (PH) |  (GS) |  (GS) |  (GS) |  (GS) |
  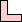 ? |  (GS) |  (GS) |  (GS) |  (PH) |
   none (PH) |  (PH) |    none (PH) |    none (PH) |    none (PH) |
   none (PH) |    none (PH) |    none (PH) |    none (PH) |    none (PH) |
 (PH) |    none (PH) |    none (PH) |    none (PH) |    none (PH) |
   none (PH) |  (PH) |    none (PH) |  (PH) |    none (PH) |
 (GS) |  (GS) |  (GS) |  (GS) |    none (PH) |
   none (PH) |    none (PH) |  (GS) |  (GS) |  (GS) |
 (GS) |    none (PH) |  (GS) |  (GS) |  (GS) |
 (GS) |  (PH) |    none (PH) |  (PH) |    none (PH) |
   none (PH) |  (PH) |    none (PH) |    none (PH) |    none (PH) |
 (PH) |    none (PH) |    none (PH) |    none (PH) |    none (PH) |
   none (PH) |    none (PH) |    none (PH) |    none (PH) |    none (PH) |
   none (PH) |  (GS) |  (GS) |  (GS) |  (GS) |
 (GS) |    none (PH) |  (GS) |    ? |  (PH) |
   none (PH) |    none (PH) |    none (PH) |  (PH) |  (PH) |
 (PH) |    none (PH) |    none (PH) |  (PH) |    none (PH) |
   none (PH) |    none (PH) |    none (PH) |    none (PH) |    none (PH) |
   none (PH) |    none (PH) |  (PH) |    none (PH) |  (GS) |
   none (PH) |    none (PH) |  (GS) |    none (PH) |    none (PH) |
 (PH) |  (PH) |  (GS) |  (PH) |  (GS) |
 (PH) |    none (PH) |    none (PH) |    none (PH) |    none (PH) |
   none (PH) |  (PH) |  (PH) |  (GS) |    none (PH) |
 (PH) |    none (PH) |    none (PH) |    none (PH) |  (GS) |
 (PH) |  (GS) |    none (PH) |  (PH) |    none (PH) |
   none (PH) |    none (PH) |    none (PH) |  (GS) |    none (PH) |
   none (PH) |    none (PH) |    none (PH) |  (GS) |    none (PH) |
   none (PH) |    none (PH) |    none (PH) |    none (PH) |  (GS) |
   none (PH) |    none (PH) |    none (PH) |    none (PH) |    none (PH) |
   none (PH) |    none (JT) |    none (PH) |    none (PH) |    none (PH) |
George Sicherman sent solutions for all the trihexes as well.

| 
| 
| 
| 
|

| 
| 
| 
| 
|
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 2/16/10.