

s = 2

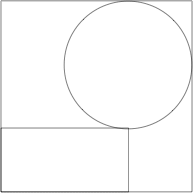
s = 2 + 8/√65 = 2.992+ (DC)


s = 3

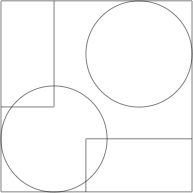
s = 18/5 = 3.6 (DC) (MM)
I suspect this is a pretty hard problem if we are allowed to tilt the cylinders, so I also offer the easier problem: What is the smallest cubical box that will fit n cylinders, each parallel to one of the sides of the box?
Here are the best-known packings of tuna cans. For each, a 3-dimensional view and a top view are provided.
2
| 3
| 6
| 7
|
8
| 9
| 10
| 16
|
18
| 19
| 20
| 21
|
22
| 24
| 30
| 31
|
32
| 33
| 34
| 35
|
36
| 37
| 40
| 41
|
42
| 44
| 46
| 54
|
1
| 2
| 3
| 8
|
10
| 12
| 16
| 20
|
27
|
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 10/24/12.