Problem of the Month (October 2019)

We say the signature of a tiling of integer squares in a rectangle is a total ordering of the set of integers that count the number of horizontally and vertically adjacent squares for each square in the tiling. For example, 1=3>2 is the signature of a tiling that has the same number of squares with 1 neighbor and 3 neighbors, which is more than the number of squares with 2 neighbors.

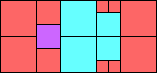
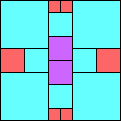
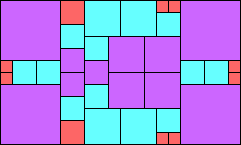
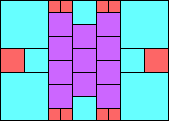
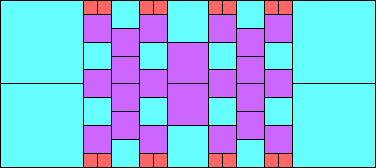
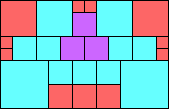
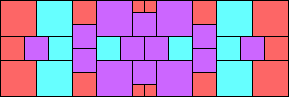
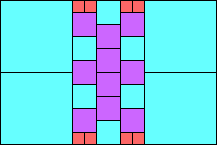
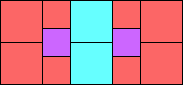
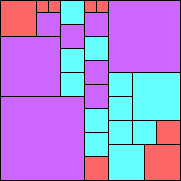
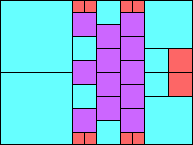
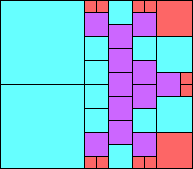
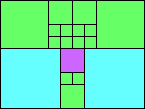
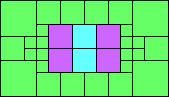
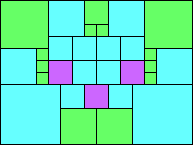
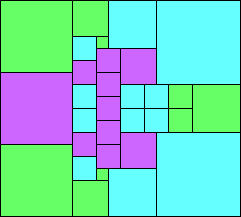
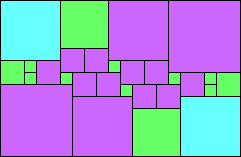
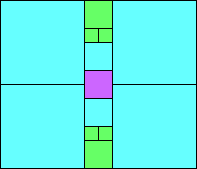
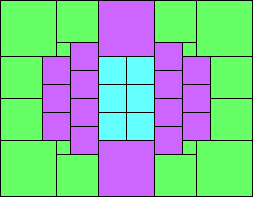
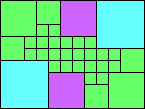
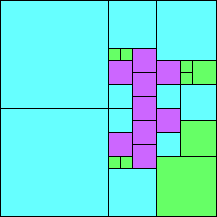
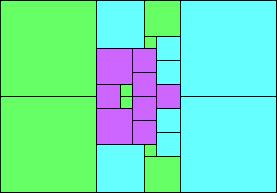
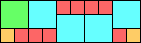
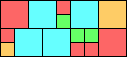
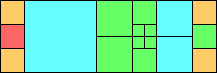
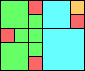
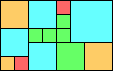
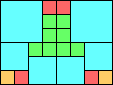
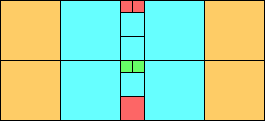
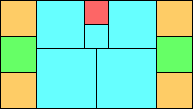
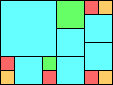
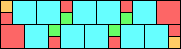
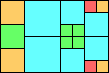
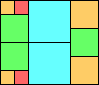
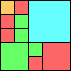
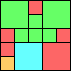
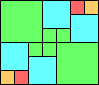
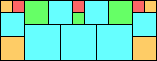
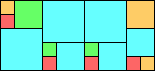
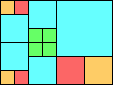
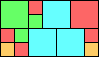
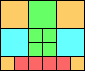
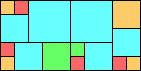
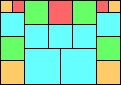
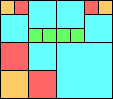
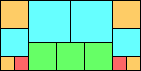
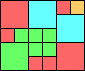
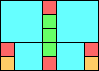
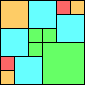
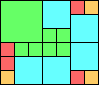
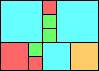
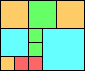
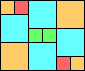
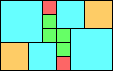
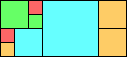
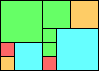
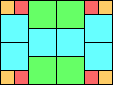
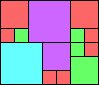
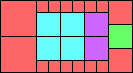
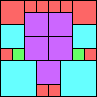
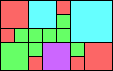
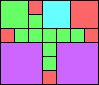
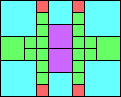
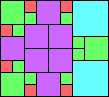
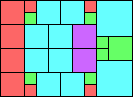
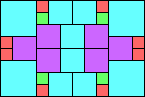
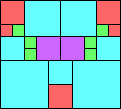
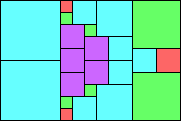
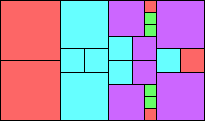
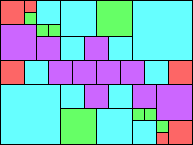
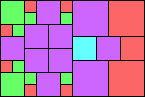
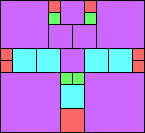
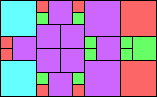
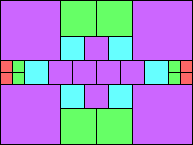
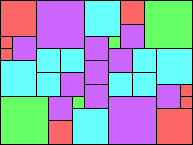
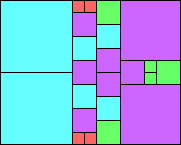
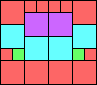
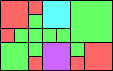
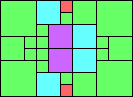
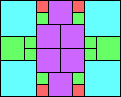
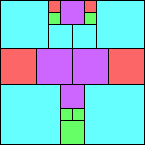
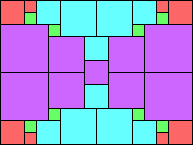
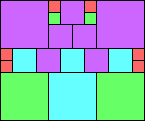
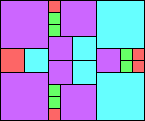
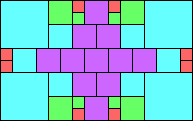
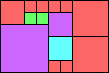
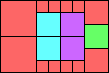
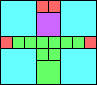
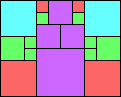
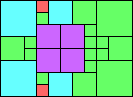
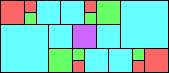
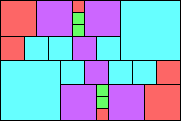
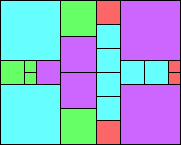
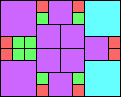
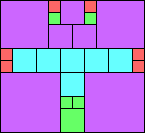
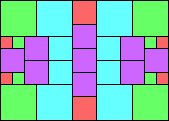
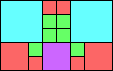
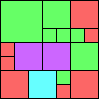
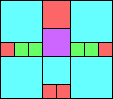
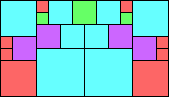
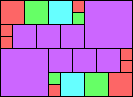
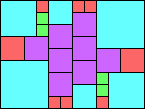
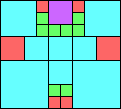
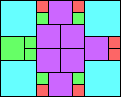
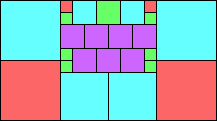
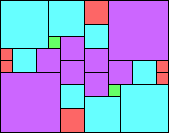
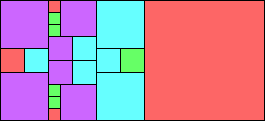
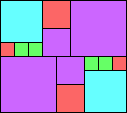
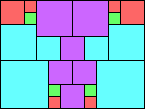
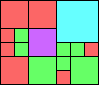
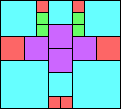
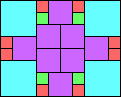
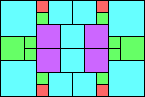
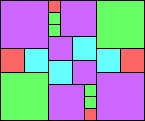
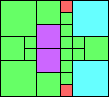
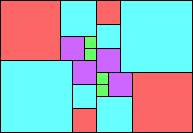
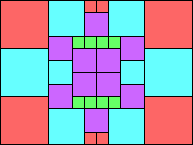
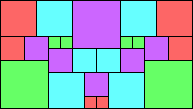
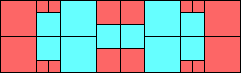
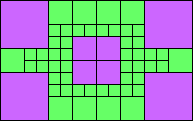
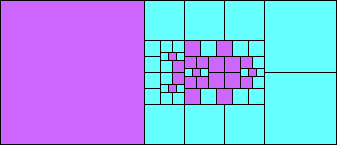
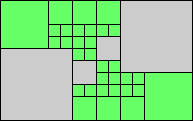
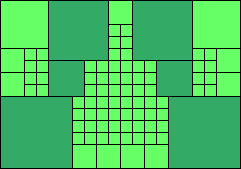
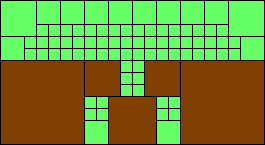
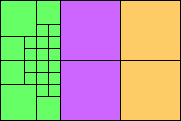
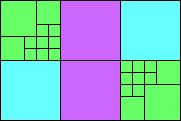
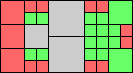
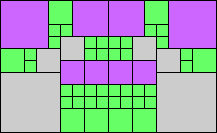
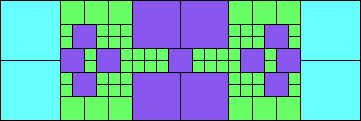
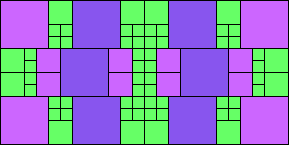
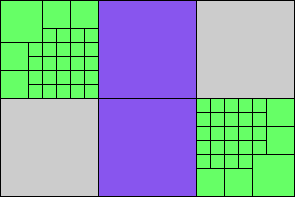
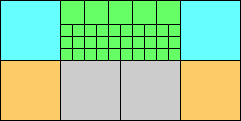
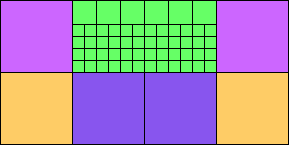
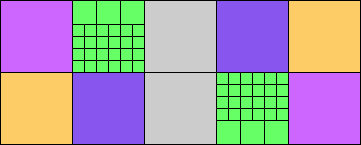
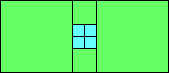
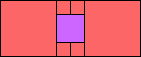
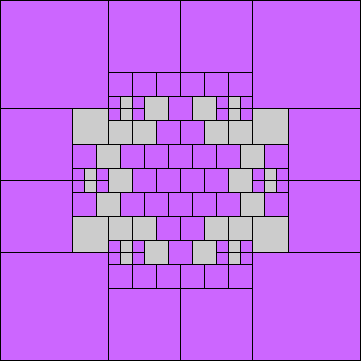
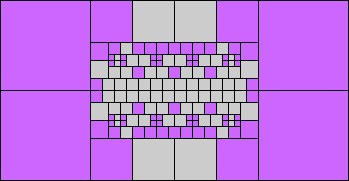
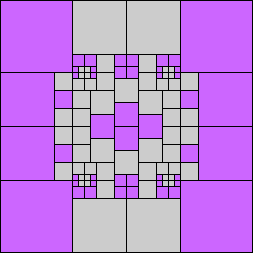
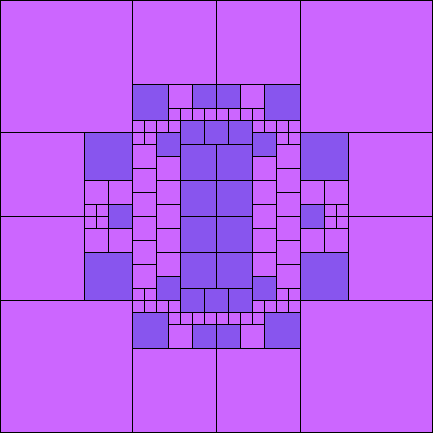
Given such a total order, what is the smallest (in terms of area, then number of squares) tiling with that signature?

ANSWERS

George Sicherman, Maurizio Morandi, Joe DeVincentis, and Bryce Herdt sent some results.

1 and 2 element sets
123
1
1
2

1>2
1=2
2>1

2
3
none
1>3 		none
1=3
3>1

2>3
2=3
3>2
none
3
4
none
1>4 		none
1=4
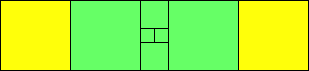
4>1

2>4
2=4
4>2

3>4
3=4
4>3
5
none
1>5 		none
1=5
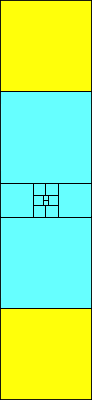
5>1 (one sixth scale)
(MM)

with lots of 2's added
2>5 and 2=5
(MM)
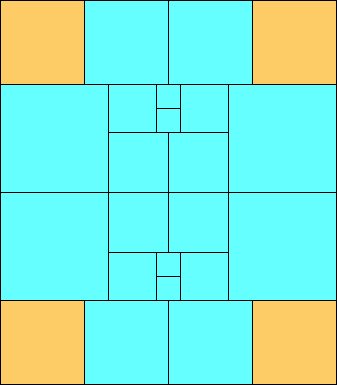
5>2
(GS)

3>5
3=5
(GS)
5>3
6
none
1>6 		none
1=6 		none
6>1
none
2>6
(JD) 		none
2=6
(JD) 		none
6>2
(JD)

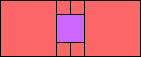
3>6
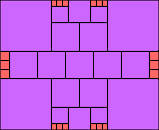
6>3 (one thirtieth scale)
(JD)

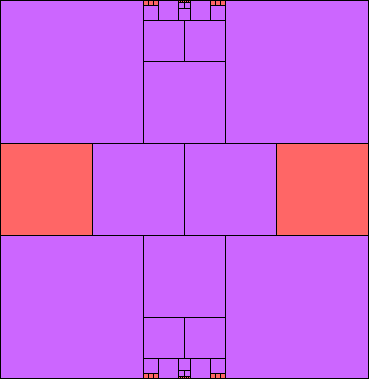
3=6 (one twelfth scale)
(JD)
7
none
1>7 		none
1=7 		none
7>1
none
2>7
(JD) 		none
2=7
(JD) 		none
7>2
(JD)

3>7
(GS) 		none
3=7
(JD) 		none
7>3
(JD)
8
none
1>8 		none
1=8 		none
8>1
none
2>8
(JD) 		none
2=8
(JD) 		none
8>2
(JD)

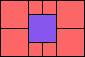
3>8
(GS) 		none
3=8
(JD) 		none
8>3
(JD)
9
none
1>9 		none
1=9 		none
9>1
none
2>9
(JD) 		none
2=9
(JD) 		none
9>2
(JD)

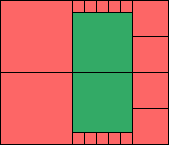
3>9
(GS) 		none
3=9
(JD) 		none
9>3
(JD)
10
none
1>10 		none
1=10 		none
10>1
none
2>10
(JD) 		none
2=10
(JD) 		none
10>2
(JD)

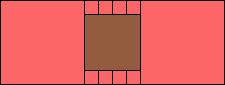
3>10
(MM) 		none
3=10
(JD) 		none
10>3
(JD)
11
none
1>11 		none
1=11 		none
11>1
none
2>11
(JD) 		none
2=11
(JD) 		none
11>2
(JD)

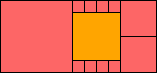
3>11
(GS) 		none
3=11
(JD) 		none
11>3
(JD)
12
none
1>12 		none
1=12 		none
12>1
none
2>12
(JD) 		none
2=12
(JD) 		none
12>2
(JD)

3>12
(MM) 		none
3=12
(JD) 		none
12>3
(JD)

45
4
4
5

4>5
4=5
(GS)
5>4
(GS)

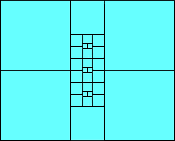
5 (one sixth scale)
(MM)
6

4>6
(GS)
4=6
(GS)
6>4
(MM)

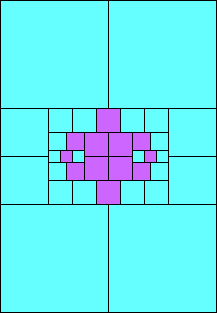
5>6 (one half scale)
(GS)
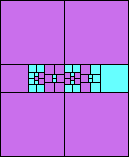
5=6 (one sixth scale)
(MM)
6>5 (one sixth scale)
(GS)
7

4>7
(GS)
4=7 (one half scale)
(MM)
7>4 (one half scale)
(MM)

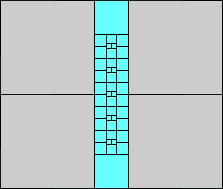
5>7 (one sixth scale) 		none
5=7
(JD) 		none
7>5
(JD)
8

4>8
(GS) 		none
4=8
(JD) 		none
8>4
(JD)

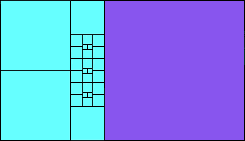
5>8 (one sixth scale)
(MM) 		none
5=8
(JD) 		none
8>5
(JD)
9

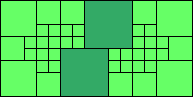
4>9
(MM) 		none
4=9
(JD) 		none
9>4
(JD)

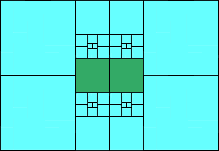
5>9 (one sixth scale)
(MM) 		none
5=9
(JD) 		none
9>5
(JD)
10

4>10
(MM) 		none
4=10
(JD) 		none
10>4
(JD)

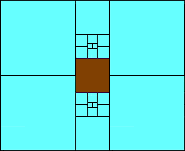
5>10 (one sixth scale)
(MM) 		none
5=10
(JD) 		none
10>5
(JD)
11

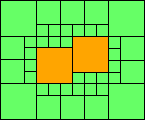
4>11
(MM) 		none
4=11
(JD) 		none
11>4
(JD)

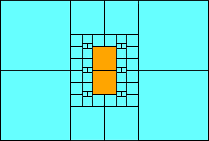
5>11 (one sixth scale)
(MM) 		none
5=11
(JD) 		none
11>5
(JD)
12

4>12
(MM) 		none
4=12
(JD) 		none
12>4
(JD)

5>12 (one sixth scale)
(MM) 		none
5=12
(JD) 		none
12>5
(JD)

{1,2,3}
none
1>2>3 		none
1>3>2 		none
2>1>3
2>3>1
3>1>2
3>2>1 		none
1=2>3 		none
1=3>2
2=3>1 		none
1>2=3
2>1=3
3>1=2 		none
1=2=3

{1,2,4}
none
1>2>4 		none
1>4>2 		none
2>1>4
2>4>1

4>1>2
4>2>1
none
1=2>4 		none
1=4>2
2=4>1 		none
1>2=4 		none
2>1=4
4>1=2 		none
1=2=4

{1,3,4}
none
1>3>4 		none
1>4>3
3>1>4
3>4>1 		none
4>1>3
4>3>1
none
1=3>4 		none
1=4>3
3=4>1 		none
1>3=4
3>1=4
4>1=3 		none
1=3=4

{2,3,4}

2>3>4
2>4>3
3>2>4
3>4>2
4>2>3
(GS)
4>3>2
2=3>4
2=4>3
3=4>2
2>3=4
3>2=4
4>2=3
2=3=4

{1,2,5}
none
1>2>5 		none
1>5>2 		none
2>1>5
(JD)
5>1>2 (one sixth scale)
(JD)
5>2>1, and with lots of 2's added, 2=5>1 and 2>5>1
(MM)
none
1=2>5 		none
1=5>2 		none
1>2=5 		none
2>1=5
(JD)
5>1=2 (one sixth scale)
(JD) 		none
1=2=5

{1,3,5}
none
1>3>5 		none
1>5>3
3>1>5
3>5>1

5>1>3 (one thirtieth scale)
(JD)
5>3>1
none
1=3>5 		none
1=5>3
3=5>1
(GS) 		none
1>3=5
3>1=5
5>1=3 (one sixth scale)
(MM) 		none
1=3=5

{2,3,5}

2>3>5
2>5>3 (one half scale)
(MM)

3>2>5
3>5>2
5>2>3
(GS)
5>3>2
(GS)

2=3>5
2=5>3
(GS)
3=5>2
2>3=5
3>2=5
5>2=3
(GS)
2=3=5

{1,4,5}
none
1>4>5
(JD) 		none
1>5>4
(JD) 		none
4>1>5
(BH)
4>5>1
(GS)
5>1>4 (one thirtieth scale)
(BH)

5>4>1
(MM) 		none
1=4>5
(JD) 		none
1=5>4
(JD)
4=5>1
(MM)
none
1>4=5
(JD)
4>1=5
(JD)
5>1=4 (one sixth scale)
(JD) 		none
1=4=5
(JD)

{2,4,5}

2>4>5
(MM)

2>5>4 (one half scale)
(MM)

4>2>5
(GS)
4>5>2
(GS)
5>2>4
(MM)
5>4>2
(GS)

2=4>5
(GS)
2=5>4 (one half scale)
(GS)
4=5>2
(GS)
2>4=5
4>2=5
5>2=4
2=4=5
(MM)

{3,4,5}

3>4>5
(GS)
3>5>4
4>3>5
4>5>3
5>3>4
(GS)
5>4>3
(GS)

3=4>5
3=5>4
4=5>3
(GS)
3>4=5
4>3=5
5>3=4
3=4=5
(GS)

{1,3,6}
none
1>3>6 		none
1>6>3
3>1>6
(GS)
3>6>1
(GS) 		none
6>1>3
6>3>1 (one sixth scale)
(JD)
none
1=3>6 		none
1=6>3
3=6>1 (one sixth scale)
(JD) 		none
1>3=6
3>1=6
(GS) 		none
6>1=3
(JD) 		none
1=3=6

{2,3,6}

2>3>6
3>2>6
3>6>2
6>3>2, and by adding 2's in the middle, 6>2=3, 6>2>3, 2=6>3, and 2>6>3 (one sixth scale)
(JD)

2=3>6
3>2=6
3=6>2, and by adding 2's in the middle, 2=3=6 and 2>3=6 (one twelfth scale)
(JD)

{1,4,6}
none
1>4>6 		none
1>6>4
4>1>6
(MM)
4>6>1 		none
6>1>4
(JD)
6>4>1 (one sixth scale)
(JD)
none
1=4>6 		none
1=6>4
4=6>1 (one sixth scale)
(JD) 		none
1>4=6
4>1=6
(GS) 		none
6>1=4
(JD) 		none
1=4=6

{2,4,6}
none
2>4>6
(JD) 		none
2>6>4
(JD)
4>2>6
4>6>2
(GS) 		none
6>2>4
(JD)
6>4>2
(GS)

2=4>6
(GS) 		none
2=6>4
(JD)
4=6>2
(GS) 		none
2>4=6
(JD)
4>2=6
6>2=4 (one half scale)
(JD)
2=4=6
(GS)

{3,4,6}

3>4>6
3>6>4
(GS)
4>3>6
4>6>3
(GS)
6>3>4
(GS)
6>4>3
(GS)

3=4>6
3=6>4
(GS)
4=6>3
(GS)
3>4=6
4>3=6
6>3=4
(GS)
3=4=6
(GS)

{1,5,6}
none
1>5>6
(JD) 		none
1>6>5
(JD)
5>1>6 (one thirtieth scale)
(BH)
5>6>1 (one sixth scale)
(JD) 		none
6>1>5
(BH)
6>5>1 (one sixth scale)
(MM)
none
1=5>6
(JD) 		none
1=6>5
(JD)
5=6>1 (one twelfth scale)
(JD) 		none
1>5=6
(JD)
5>1=6 (one sixth scale)
(MM) 		none
6>1=5
(JD) 		none
1=5=6
(JD)

{2,5,6}

5>2>6
(GS)
5>6>2
(GS)
6>5>2 (one sixth scale)
(JD)
5>2=6
(GS)

5=6>2, and with 2's added, 2=5=6, and 2>5=6 (one twelfth scale) (JD)
on both ends with lots of 2's between them
6>2=5 and 6>2>5
(one sixth scale) (JD)

on both ends with lots of 2's between them
2=6>5 and 2>6>5
(one sixth scale) (JD)
on both ends with lots of 2's between them
2=5>6 and 2>5>6
(one sixth scale) (JD)

{3,5,6}

3>5>6
(GS)
3>6>5
(GS)
5>3>6
(GS)
5>6>3
(GS)
6>3>5
(MM)
6>5>3
(JD)

3=5>6
(GS)
3=6>5
(GS)
5=6>3
(GS)
3>5=6
5>3=6
(GS)
6>3=5
(GS)
3=5=6
(GS)

{4,5,6}

4>5>6
(GS)
4>6>5
(GS)
5>4>6
(GS)
5>6>4
(GS)

6>4>5
(GS)
6>5>4
(GS)

4=5>6
(MM)
4=6>5
(JD)
5=6>4
(GS)

4>5=6
(GS)
5>4=6
(GS)
6>4=5
(GS)
4=5=6
(GS)

{1,2,3,4}
none
1>2>3>4 		none
1>2>4>3 		none
1>3>2>4 		none
1>3>4>2 		none
1>4>2>3 		none
1>4>3>2
none
2>1>3>4 		none
2>1>4>3
2>3>1>4
2>3>4>1 		none
2>4>1>3
2>4>3>1
none
3>1>2>4 		none
3>1>4>2
3>2>1>4
3>2>4>1
3>4>1>2
3>4>2>1
none
4>1>2>3 		none
4>1>3>2 		none
4>2>1>3
4>2>3>1
(MM)
4>3>1>2
4>3>2>1
none
1>2>3=4 		none
1>3>2=4 		none
1>4>2=3 		none
2>1>3=4
2>3>1=4
2>4>1=3

3>1>2=4
3>2>1=4
3>4>1=2 		none
4>1>2=3
4>2>1=3
(GS)
4>3>1=2
(GS)
none
1>2=3>4 		none
1>2=4>3 		none
1>3=4>2 		none
2>1=3>4
(JD) 		none
2>1=4>3
2>3=4>1

3>1=2>4
3>1=4>2
3>2=4>1 		none
4>1=2>3
4>1=3>2
4>2=3>1
none
1=2>3>4 		none
1=2>4>3 		none
1=3>2>4 		none
1=3>4>2 		none
1=4>2>3 		none
1=4>3>2

2=3>1>4
2=3>4>1 		none
2=4>1>3
2=4>3>1
3=4>1>2
3=4>2>1
none
1=2=3>4
(JD) 		none
1=2=4>3 		none
1=3=4>2
(JD)
2=3=4>1 		none
1=2>3=4 		none
1=3>2=4
(JD) 		none
1=4>2=3
2=3>1=4

2=4>1=3
3=4>1=2 		none
1>2=3=4
2>1=3=4
3>1=2=4
4>1=2=3 		none
1=2=3=4
(JD)

{2,3,4,5}

2>3>4>5
2>3>5>4
2>4>3>5
2>4>5>3 (one half scale)
(GS)

2>5>3>4 (one half scale)
(MM)
2>5>4>3 (one half scale)
(GS)

3>2>4>5
3>2>5>4
3>4>2>5
3>4>5>2
3>5>2>4
3>5>4>2

4>2>3>5
4>2>5>3
(GS)
4>3>2>5
4>3>5>2
4>5>2>3
4>5>3>2

5>2>3>4
(GS)
5>2>4>3
(GS)
5>3>2>4
5>3>4>2
(GS)
5>4>2>3
(GS)
5>4>3>2

2>3>4=5
(GS)
2>4>3=5
2>5>3=4
(GS)
3>2>4=5
3>4>2=5
3>5>2=4

4>2>3=5
4>3>2=5
4>5>2=3
5>2>3=4
(GS)
5>3>2=4
5>4>2=3

2>3=4>5
2>3=5>4
(MM)
2>4=5>3
(GS)
3>2=4>5
3>2=5>4
(GS)
3>4=5>2

4>2=3>5
4>2=5>3
4>3=5>2
5>2=3>4
5>2=4>3
(GS)
5>3=4>2

2=3>4>5
2=3>5>4
2=4>3>5
2=4>5>3 (one half scale)
(GS)
2=5>3>4
(GS)
2=5>4>3

3=4>2>5
3=4>5>2
3=5>2>4
3=5>4>2
4=5>2>3
4=5>3>2

2=3=4>5
2=3=5>4
2=4=5>3
3=4=5>2
2=3>4=5
2=4>3=5
2=5>3=4
3=4>2=5
3=5>2=4
4=5>2=3

2>3=4=5
3>2=4=5
4>2=3=5
5>2=3=4
2=3=4=5

{3,4,5,6}

3>4>5>6
3>4>6>5
3>5>4>6
3>5>6>4
(GS)
3>6>4>5
3>6>5>4
(GS)

4>3>5>6
4>3>6>5
4>5>3>6
(GS)
4>5>6>3
(GS)
4>6>3>5
(GS)
4>6>5>3
(GS)

5>3>4>6
(GS)
5>3>6>4
(GS)
5>4>3>6
(GS)
5>4>6>3
(GS)
5>6>3>4
(GS)
5>6>4>3
(GS)

6>3>4>5
(GS)
6>3>5>4
(GS)
6>4>3>5
(GS)
6>4>5>3
(GS)
6>5>3>4
(GS)
6>5>4>3
(GS)

3>4>5=6
3>5>4=6
(GS)
3>6>4=5
(GS)
4>3>5=6
4>5>3=6
(GS)
4>6>3=5
(GS)

5>3>4=6
(GS)
5>4>3=6
(GS)
5>6>3=4
(GS)
6>3>4=5
(GS)
6>4>3=5
(GS)
6>5>3=4
(GS)

3>4=5>6
(GS)
3>4=6>5
(GS)
3>5=6>4
(GS)
4>3=5>6
(GS)
4>3=6>5
(GS)
4>5=6>3
(GS)

5>3=4>6
(GS)
5>3=6>4
(GS)
5>4=6>3
(GS)
6>3=4>5
(GS)
6>3=5>4
(GS)
6>4=5>3
(GS)

3=4>5>6
3=4>6>5
3=5>4>6
3=5>6>4
(GS)
3=6>4>5
(GS)
3=6>5>4
(GS)

4=5>3>6
(GS)
4=5>6>3
(GS)
4=6>3>5
(GS)
4=6>5>3
(GS)
5=6>3>4
(GS)
5=6>4>3
(MM)

3=4=5>6
(GS)
3=4=6>5
3=5=6>4
(GS)
4=5=6>3
(GS)

3=4>5=6
3=5>4=6
(GS)
3=6>4=5
(GS)
4=5>3=6
(GS)
4=6>3=5
(GS)
4=6>3=5
(GS)

3>4=5=6
4>3=5=6
(GS)
5>3=4=6
(GS)
6>3=4=5
(GS)
3=4=5=6
(GS)

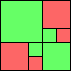
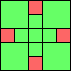
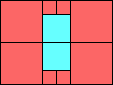
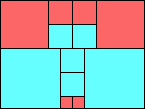
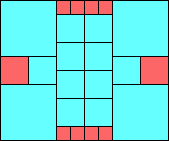
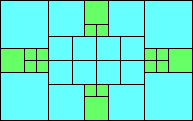
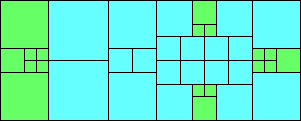
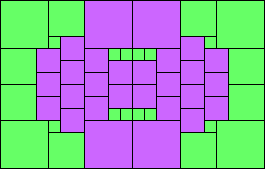
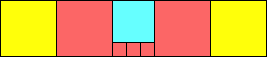
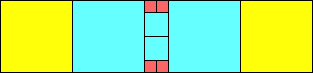
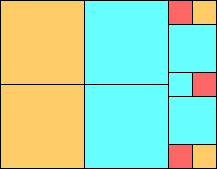
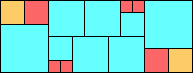
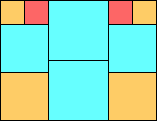
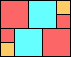
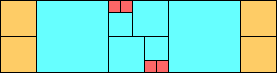
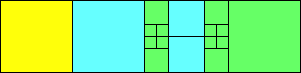
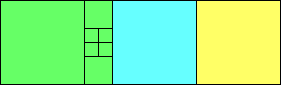
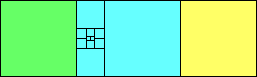
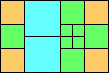
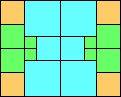
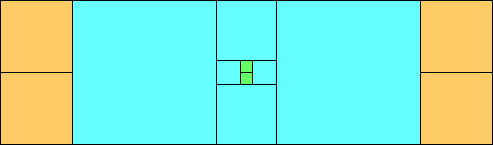
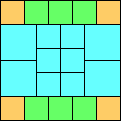
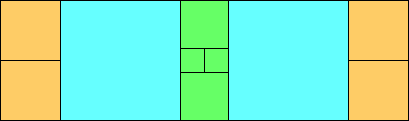
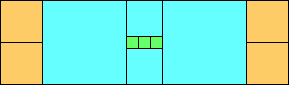
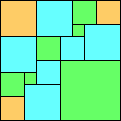
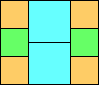
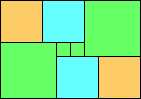
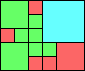
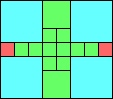
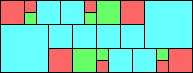
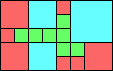
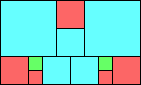
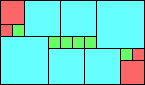
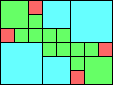
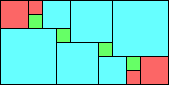
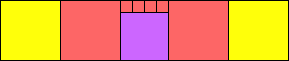
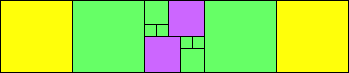
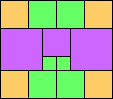
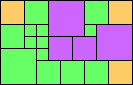
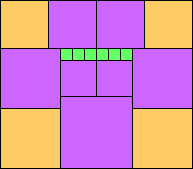
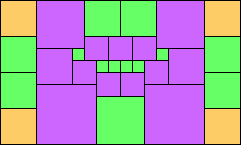
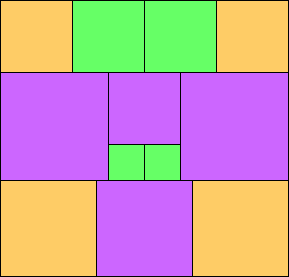
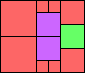
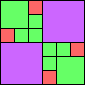
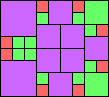
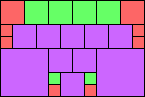
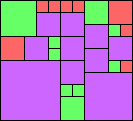
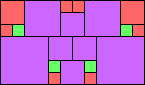
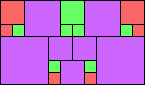
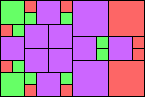
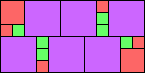
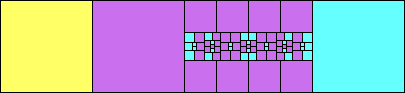
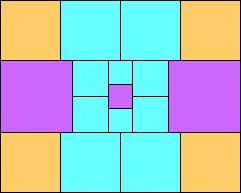
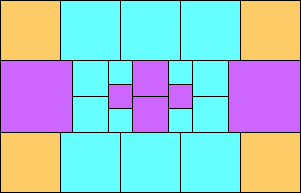
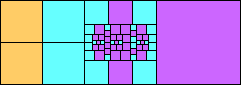
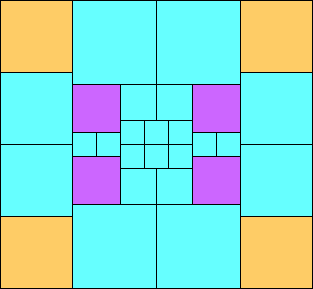
George Sicherman suggested the variant problem of looking for small square tilings of rectangles where the differently colored squares have equal area. Here are the best known results:

{n} and {m,n}
m \ n12345
1
2
3 none none
4 none
(GS)
5 none ?
(GS)
(one sixth scale)
(MM)
6 none none
(GS)
(GS)
(one third scale)
(GS)
7 none none ?
(GS) 		?
8 none none ? ?
9 none none ?
(GS) 		?
10 none none
(one half scale)
(GS) 		?
11 none none
(one half scale)
(GS) 		?
12 none none ? ?

3-Element Sets
{1,3,4}
{2,3,4}
{3,4,5}

(GS) 		{2,3,6}

(GS) 		{2,4,6}
{3,4,6}

(GS)
{3,5,6}

(GS) 		{4,5,6}
{3,4,7}

(GS) 		{3,5,7}

(one half scale) (GS)
{4,5,7}

(GS) 		{3,6,7}

(one half scale) (GS) 		{4,6,7}

(GS)
{2,4,8}
{3,4,8}

(GS) 		{3,5,8}

(GS)
{4,5,8}

(GS) 		{4,6,8}

(GS) 		{4,7,8}

4-Element Sets
{1,2,3,4}

(GS) 		{2,3,4,5}

(GS) 		{2,3,4,6}
{2,3,5,6}

(GS)
{1,4,5,6}

(GS) 		{3,4,5,6}
{2,3,4,7}

(GS)
{2,4,5,7}
{1,3,4,8}

(GS)
{2,3,4,8}

(GS) 		{2,4,6,8}
{3,4,7,8}

Larger Sets
{1,2,4,5,6}

(GS) 		{1,3,4,5,6}

(GS)
{1,2,3,4,8}

(GS) 		{2,4,6,7,8}
{2,3,4,5,6,7}

(one half scale) (GS) 		{1,2,3,4,5,6,7}

(one half scale) (GS)

We also investigated what the answers to the original problem would be if adjacencies at corners counted:

1 and 2 element sets
12345
1
1
2

1>2

1=2

2>1

2
3
none
1>3
none
1=3

3>1

2>3

2=3

3>2

3
4
none
1>4
none
1=4

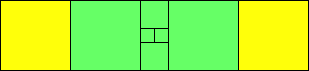
4>1

2>4

2=4

4>2

3>4

3=4

4>3
?
4
5
none
1>5
none
1=5

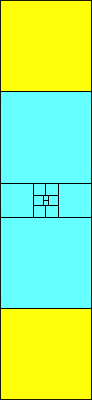
5>1 (one sixth scale)
(MM)

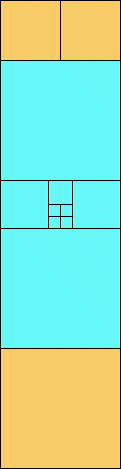
at both ends with lots of 2's in between
2>5 and 2=5
(GS)

5>2
(GS)

3>5

3=5

5>3

4>5
(GS)

4=5
(GS)

5>4
(GS)
?
5
6
none
1>6
none
1=6
?
6>1
?
2>6
?
2=6
?
6>2

3>6

3=6

6>3

4>6

4=6 (one half scale)
(GS)

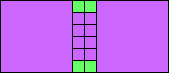
6>4
(GS)

5>6 (one half scale)
(GS)
?
5=6
?
6>5
7
none
1>7
none
1=7
?
7>1
?
2>7
?
2=7
?
7>2

3>7
(GS)
?
3=7
?
7>3

4>7

4=7
(GS)

7>4
(MM)

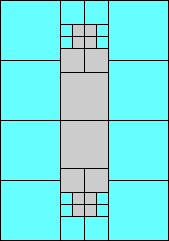
5>7
(GS)

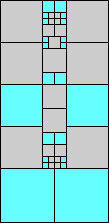
5=7 (one half scale)
(GS)

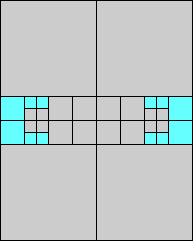
7>5
(GS)
8
none
1>8
none
1=8
?
8>1
?
2>8
?
2=8
?
8>2

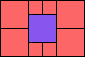
3>8
?
3=8
?
8>3

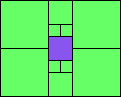
4>8
(GS)
?
4=8
?
8>4

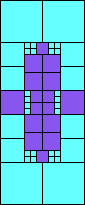
5>8 (one half scale)
(GS)
?
5=8
?
8>5
9
none
1>9
none
1=9
?
9>1
?
2>9
?
2=9
?
9>2

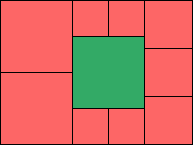
3>9
(GS)
?
3=9
?
9>3

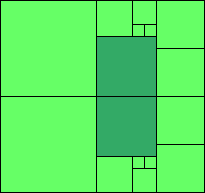
4>9
(GS)
?
4=9
?
9>4

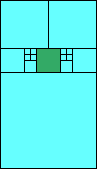
5>9 (one half scale)
(GS)
?
5=9
?
9>5
10
none
1>10
none
1=10
?
10>1
?
2>10
?
2=10
?
10>2

3>10
(GS)
?
3=10
?
10>3
?
4>10
?
4=10
?
10>4

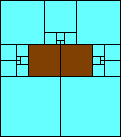
5>10 (one third scale)
(GS)
?
5=10
?
10>5
11
none
1>11
none
1=11
?
11>1
?
2>11
?
2=11
?
11>2

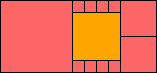
3>11
(GS)
?
3=11
?
11>3
?
4>11
?
4=11
?
11>4

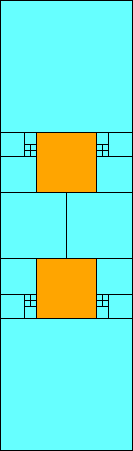
5>11 (one half scale)
(GS)
?
5=11
?
11>5
11
none
1>12
none
1=12
?
12>1
?
2>12
?
2=12
?
12>2

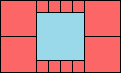
3>12
(GS)
?
3=12
?
12>3
?
4>12
?
4=12
?
12>4

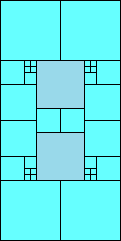
5>12 (one half scale)
(GS)
?
5=12
?
12>5

67
6 ?
6
7

6>7
(GS)

6=7 (one half scale)
(GS)

7>6 (one half scale)
(GS)
?
7
8

6>8
(GS)
?
6=8
?
8>6
?
7>8
?
7=8
?
8>7

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 10/14/19.