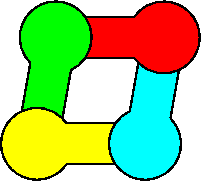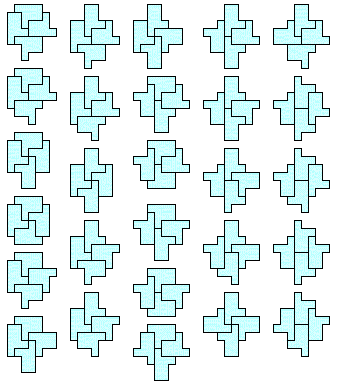Problem of the Month (November 2004)
A couple months ago, when we studied polypolyforms, Jeremy Galvagni suggested a variant of the problem that I thought was worth being a problem of the month in its own right. Given a shape S, find the smallest shape that can be tiled by S in more than one way. We call these shapes Galvagni Figures. Mike Reid was interested in such tilings without holes. Thus we call such figures Reid Figures.
Corey Plover was interested in such tilings that did not allow reflections of the tile. Thus we call such figures Plover Figures.
What are the Galvagni, Reid, and Plover Figures for small polyforms? What can be proved about such things?
ANSWERS
Some solutions for Galvagni number 2 first appeared in Puzzle Fun 11.
Many people worked on these problems and sent solutions. The attributions below indicate who did the most work on any given problem, but it was rare for one person to do it all.
Mike Reid pointed out that there are shapes with infinitely many minimal solutions:
Joseph DeVincentis and Mike Reid proved that all numbers larger than 1 are the Galvagni number of some polyomino. Mike's construction on the left uses unions of 2x2 squares to make Galvagni number 5. Mike Reid used the same idea (with 3x3 squares) to generate a shape whose only minimal configuration is asymmetrical, on the right.
Corey Plover searched polyominoes for a shape that had a large number of possible minimal solutions. His best yielded 23 solutions. Then Mike Reid found this polyomino with 27 different minimal configurations:
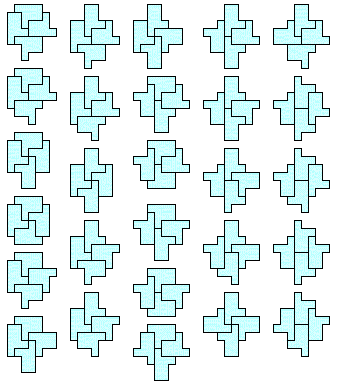
|
POLYIAMONDS
The generalized 3-iamonds are here.
|
POLYABOLOES
|
POLYOMINOES
|
POLYOCTS
|
POLYNONS
|
POLYDECS
|
George Sicherman has many pages devoted to this problem here.
If you can extend any of these results, please
e-mail me.
Click here to go back to Math Magic. Last updated 7/20/09.