Problem of the Month (November 2016)

What is the largest area that can be filled in a regular hexagon by m regular hexagons of one size and n regular hexagons of another size if none of the hexagons overlap?

ANSWERS

George Sicherman, Maurizio Morandi, and Joe DeVincentis sent improvements.

Here are the best known answers:

m \ n2345678
0
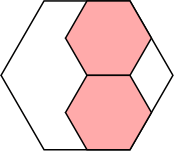
1/2 = .500
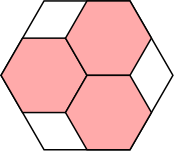
3/4 = .750
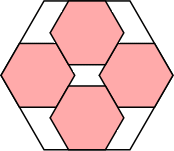
36/49 = .734+
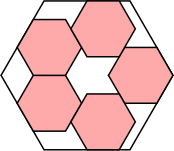
45/64 = .703+
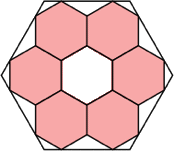
18/25 = .720
(Maurizio Morandi)
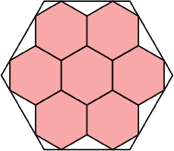
21/25 = .840
(Maurizio Morandi)
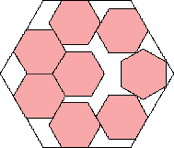
432/(446+85√3) = .728+
(Maurizio Morandi)
2
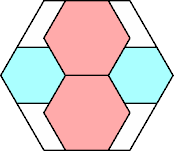
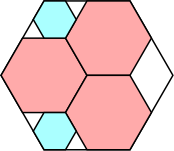
25/32 = .781+
(George Sicherman)
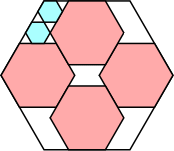
7/8 = .875
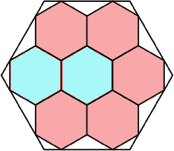
38/49 = .775+
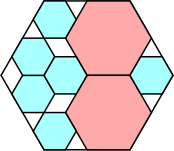
21/25 = .840
(Maurizio Morandi)
7/8 = .875+
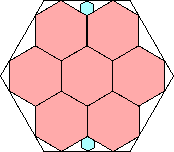
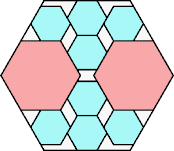
171/200 = .855
(Maurizio Morandi)
144/169 = .852+
(George Sicherman)
3
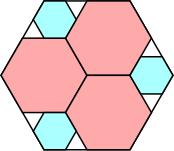
15/16 = .937+
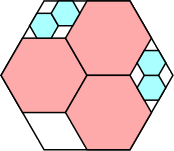
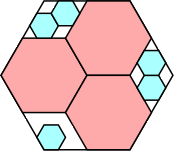
31/36 = .861+
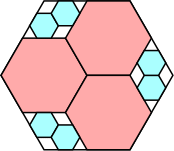
8/9 = .888+
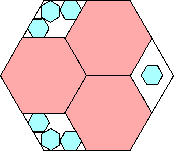
11/12 = .916+
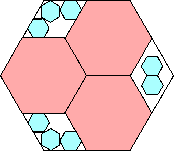
.862+
(Maurizio Morandi)
.878+
(Maurizio Morandi)
4
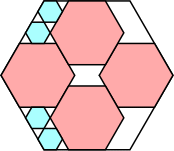
40/49 = .816+
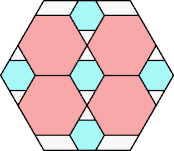
21/25 = .840
(George Sicherman)
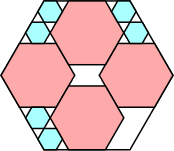
42/49 = .857+
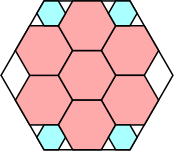
8/9 = .888+
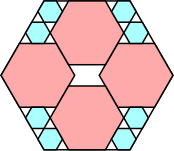
44/49 = .897+
5
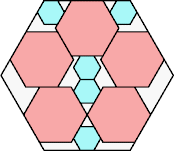
290/361 = .803+
(George Sicherman)
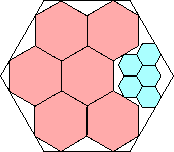
1007/1225 = .822+
(Maurizio Morandi)
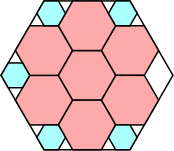
11/12 = .916+
53/64 = .828+
(George Sicherman)
6
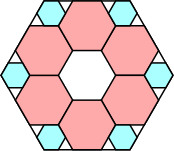
5/6 = .833+
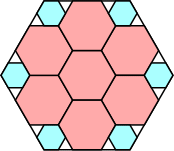
17/18 = .944+
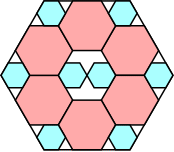
8/9 = .888+
7
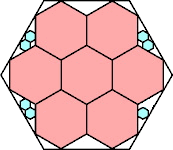
546/625 = .873+
(Maurizio Morandi)
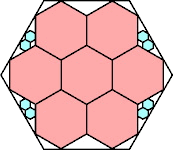
549/625 = .878+
(George Sicherman)
8
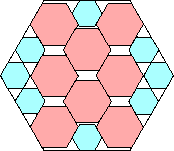
712/841 = .846+
(Maurizio Morandi)

m \ n9101112131415
0
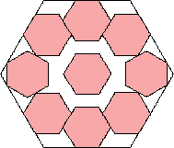
729/(24+5√3)2 = .683+
(Maurizio Morandi)
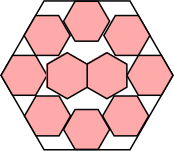
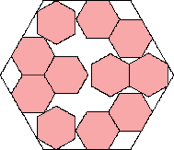
70–40√3 = .717+
(Maurizio Morandi)
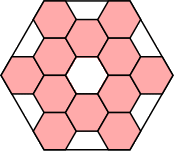
66(2–√3)/25 = .707+
(Maurizio Morandi)
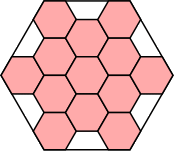
12/16 = .750
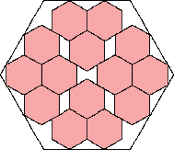
13/16 = .812+
1050/1369 = .766+
(Maurizio Morandi)
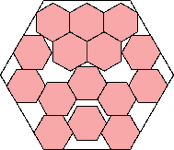
13500/(73+35√3)2 = .756+
(Maurizio Morandi)
2
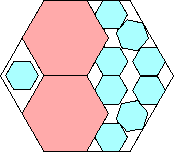
.819+
(Maurizio Morandi)
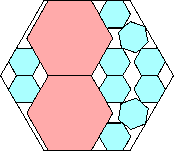
.835+
(Maurizio Morandi)
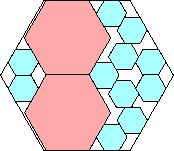
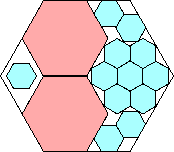
1339/1600 = .836+
(Maurizio Morandi)
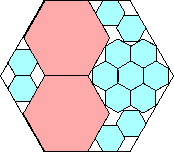
.858+
(Maurizio Morandi)
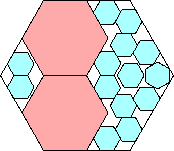
.879+
(Maurizio Morandi)
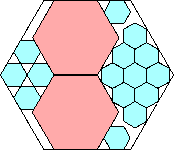
.844+
(Maurizio Morandi)
.853+
(Maurizio Morandi)
3
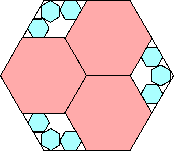
.894+
(Maurizio Morandi)
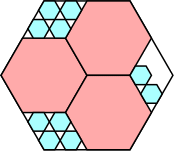
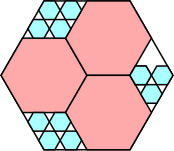
29/32 = .906+
59/64 = .921+
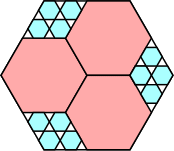
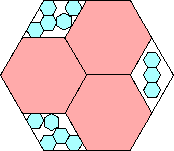
15/16 = .937+
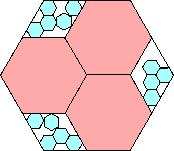
.882+
(Maurizio Morandi)
.892
(Maurizio Morandi)
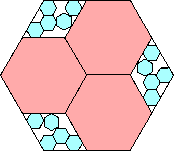
.902
(Maurizio Morandi)
4
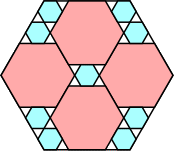
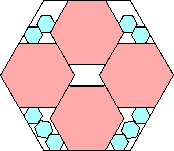
45/49 = .918+
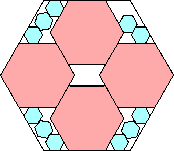
.850+
(Maurizio Morandi)
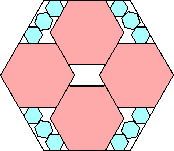
.862+
(Maurizio Morandi)
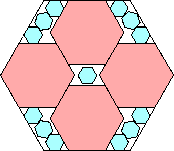
.873+
(Maurizio Morandi)
.885+
(Maurizio Morandi)
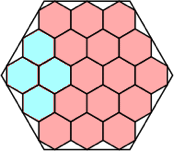
.866+
(Maurizio Morandi)
57/64 = .890+
(Maurizio Morandi)
5
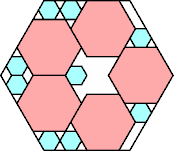
27/32 = .843+
(George Sicherman)
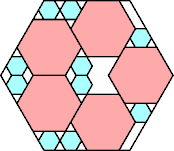
55/64 = .859+
(George Sicherman)
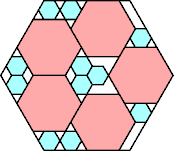
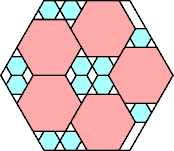
7/8 = .875
(George Sicherman)
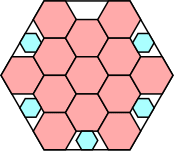
57/64 = .890+
(George Sicherman)
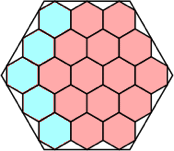
57/64 = .890+
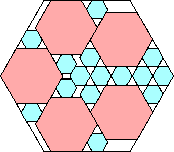
57/64 = .890+
(Maurizio Morandi)
108/125 = .864
(Maurizio Morandi)
6
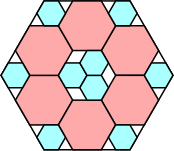
11/12 = .916+
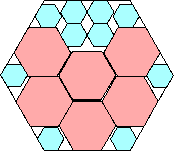
16560/18769 = .882+
(Maurizio Morandi)
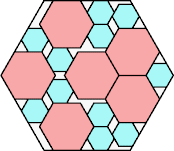
315/361 = .872+
(George Sicherman)
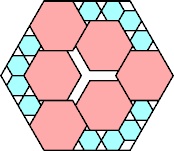
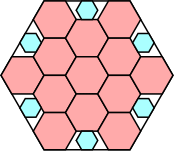
22/25 = .880
(George Sicherman)
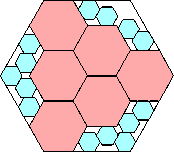
29/32 = .906+
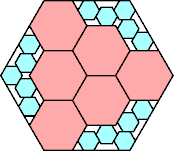
85/96 = .885+
(Maurizio Morandi)
173/192 = .901+
(George Sicherman)
7
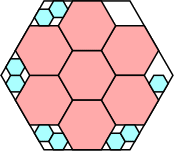
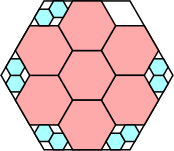
8/9 = .888+
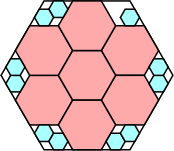
73/81 = .901+
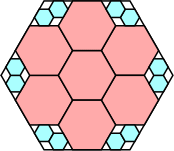
74/81 = .913+
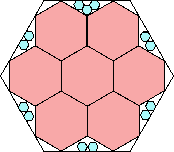
25/27 = .925+
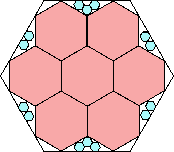
2217/2500 = .886+
(Maurizio Morandi)
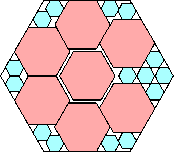
1113/1250 = .890+
(Maurizio Morandi)
351/392 = .895+
(Maurizio Morandi)
8
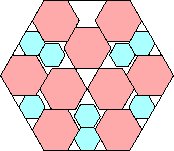
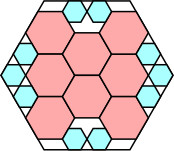
929/1089 = .853+
(Maurizio Morandi)
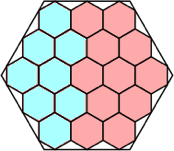
6/7 = .857+
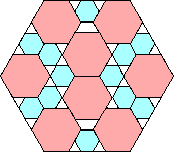
57/64 = .890+
(Maurizio Morandi)
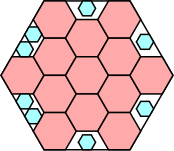
44/49 = .897+
(Maurizio Morandi)
357/400 = .892+
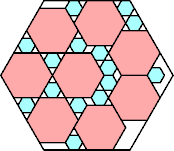
43/50 = .860
(George Sicherman)
87/100 = .870
(George Sicherman)
9
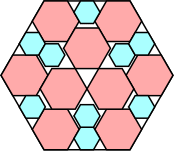
106/121 = .876+
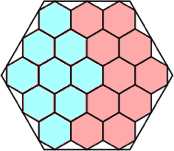
57/64 = .890+
(Maurizio Morandi)
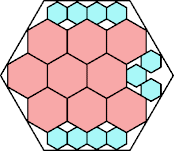
141/169 = .834+
(George Sicherman)
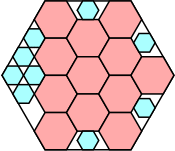
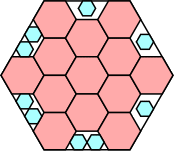
57/64 = .890+
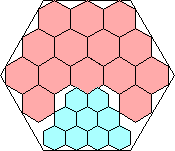
361/400 = .902+
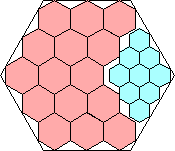
27/32 = .843+
(Joe DeVincentis)
3555/4096 = .867+
(Joe DeVincentis)
10
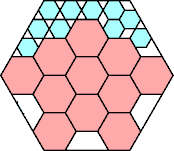
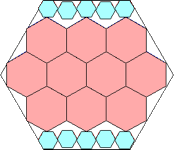
285/338 = .843+
(Joe DeVincentis)
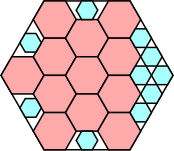
27/32 = .843+
(Joe DeVincentis)
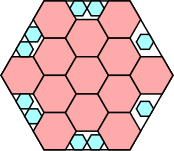
29/32 = .906+
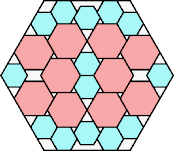
73/80 = .912+
146/169 = .863+
(George Sicherman)
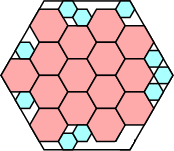
70/81 = .864+
(Joe DeVincentis)
11
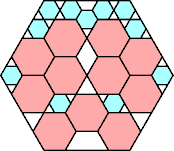
55/64 = .859+
(George Sicherman)
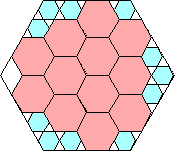
59/64 = .921+
(Joe DeVincentis)
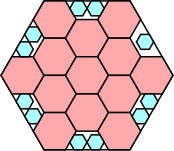
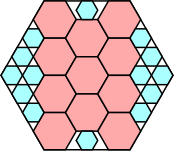
369/400 = .922+
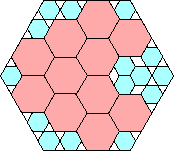
29/32 = .906+
59/64 = .921+
(Maurizio Morandi)
12
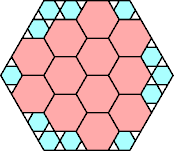
15/16 = .937
(George Sicherman)
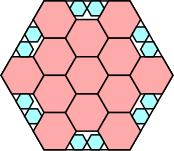
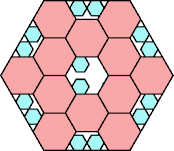
373/400 = .932+
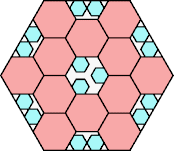
89/100 = .890
(Joe DeVincentis)
9/10 = .900
(George Sicherman)
13
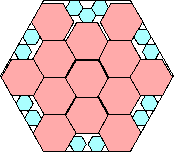
24128/26569 = .908+
(Maurizio Morandi)
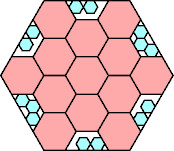
131/144 = .909+
(Joe DeVincentis)
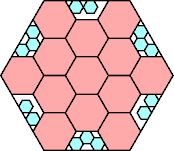
11/12 = .916+
(George Sicherman)
14
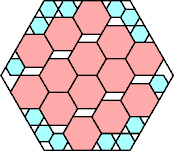
70/81 = .864+
(George Sicherman)
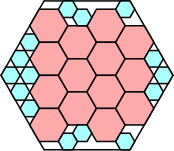
71/81 = .876+
(Joe DeVincentis)
15
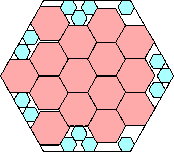
1160/1323 = .876+
(Maurizio Morandi)

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 11/23/16.