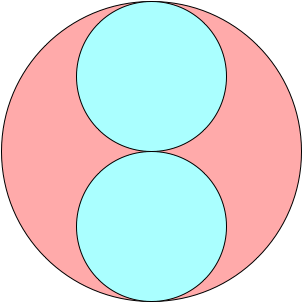
r = 1/2 = .500
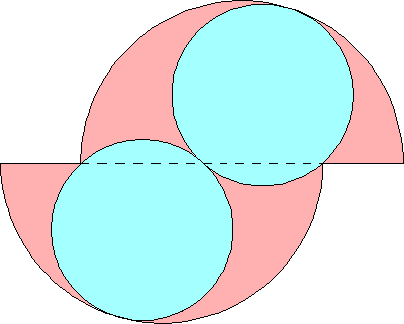
r = 9/16 = .562+
Maurizio Morandi

r = .611+
Maurizio Morandi
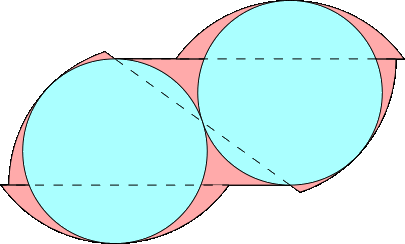
r = .656+
Joe DeVincentis
n=0 r = 1/2 = .500 | n=1 r = 9/16 = .562+ Maurizio Morandi n=2 |  r = .611+ Maurizio Morandi n=3 |  r = .656+ Joe DeVincentis |
n=0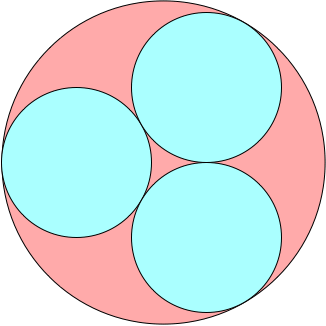 r = 2√3–3 = .464+ | n=1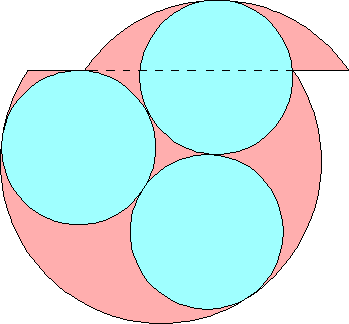 r = .478+ Maurizio Morandi n=2 | 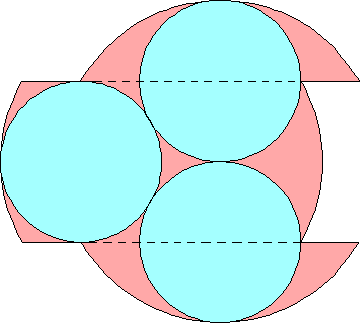 r = 1/2 = .500 Maurizio Morandi n=3 | 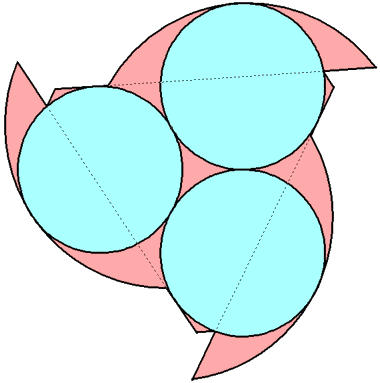 r = .510+ Jeremy Galvagni |
n=0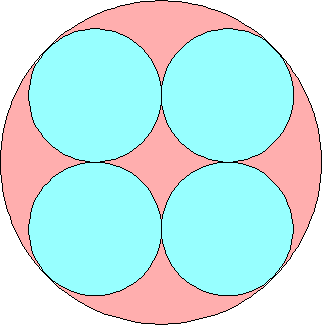 r = √2–1 = .414+ | n=1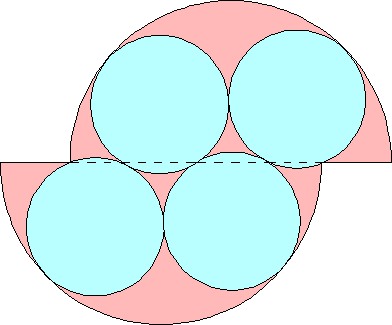 r = .427+ Maurizio Morandi | n=2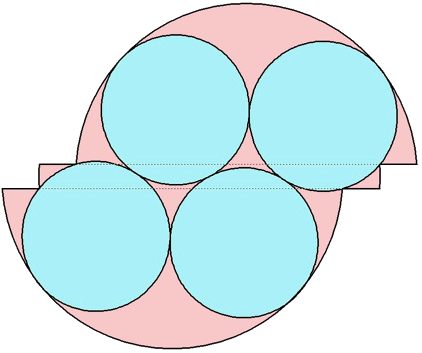 r = .433+ Jeremy Galvagni |
n=0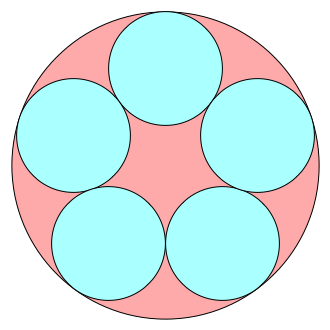 r = .370+ | n=1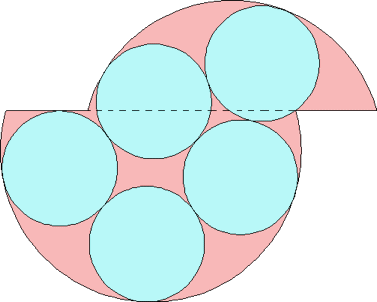 r = .382+ Maurizio Morandi |
n=0, 1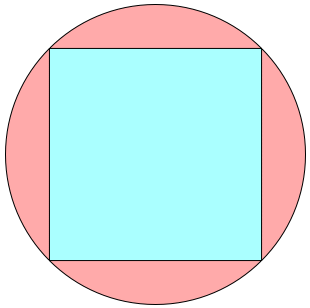 s = √2 = 1.414+ | n=2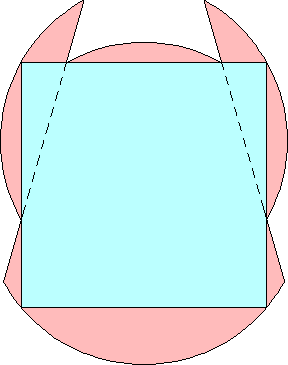 s = 1.523+ Maurizio Morandi n=3 | 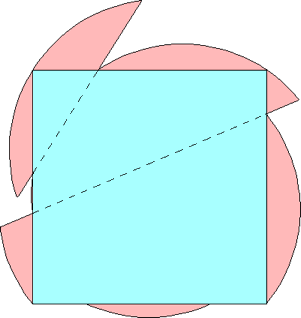 s = 1.551+ Maurizio Morandi n=4 | 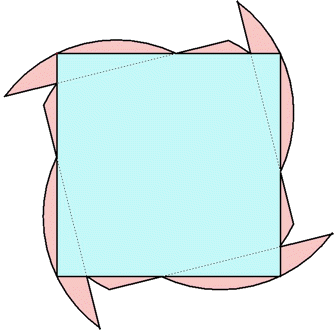 s = 1.614+ Jeremy Galvagni |
n=0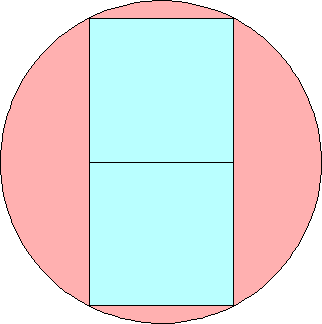 s = 2/√5 = .894+ | n=1 s = .985+ Maurizio Morandi n=2 |  s = 1.035+ Maurizio Morandi n=3 | 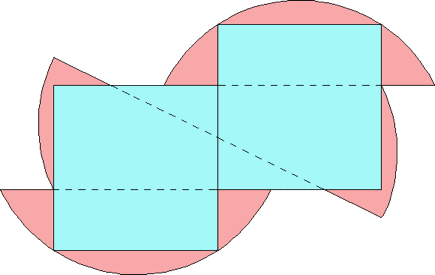 s = 1.090+ Maurizio Morandi |
n=0 s = 16/5√17 = .776+ | n=1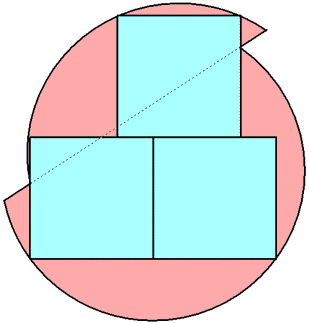 s = .808+ Jeremy Galvagni | n=2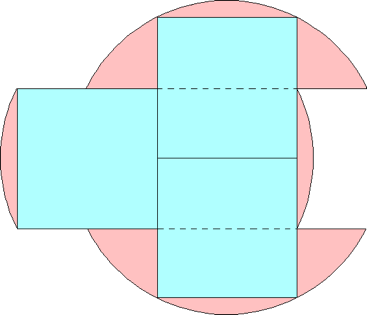 s = 2/√5 = .894+ Maurizio Morandi |
n=0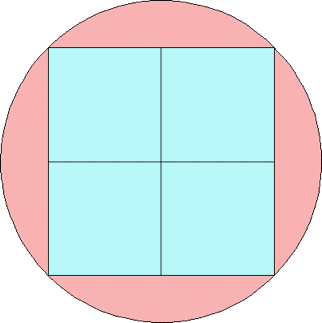 s = 1/√2 = .707+ | n=1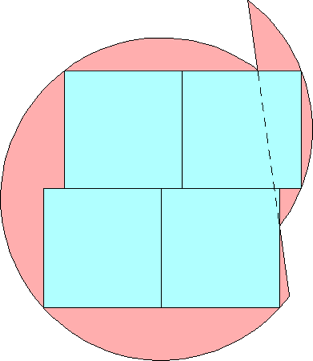 s = .736+ Maurizio Morandi |
n=0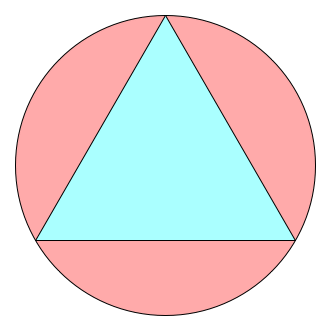 s = √3 = 1.732+ | n=1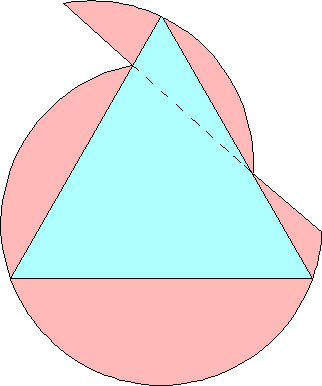 s = 1.882+ Maurizio Morandi | n=2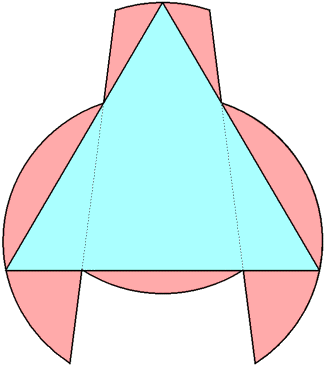 s = 2.122+ Jeremy Galvagni n=3 | 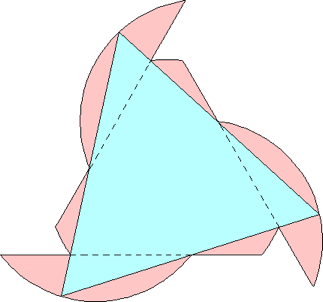 s = 2.237+ Maurizio Morandi n=4 | 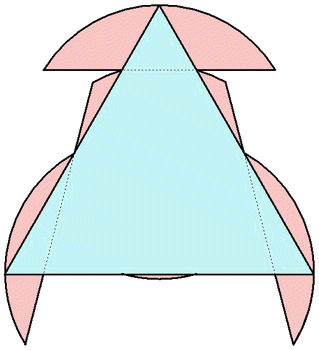 s = 2.265+ Jeremy Galvagni |
n=0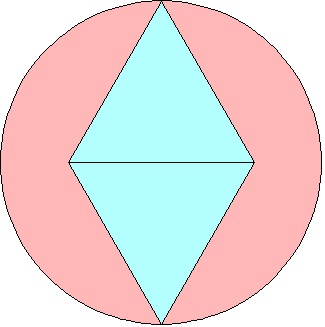 s = 2/√3 = 1.154+ | n=1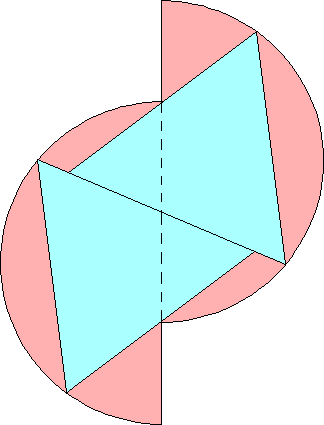 s = 1.462+ Maurizio Morandi n=2 | 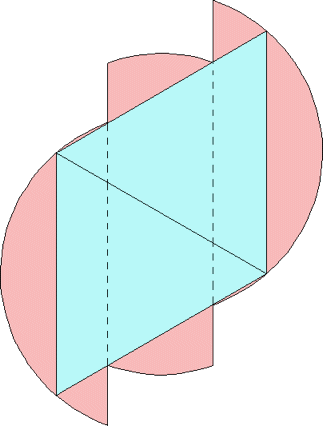 s = 4/√7 = 1.511+ Maurizio Morandi n=3 | 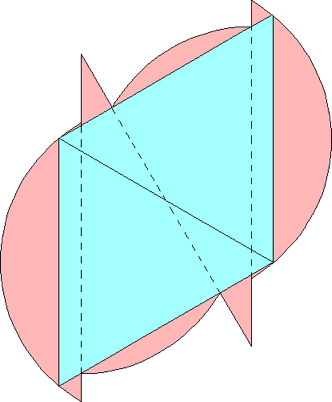 s = 1.543+ Maurizio Morandi |
n=0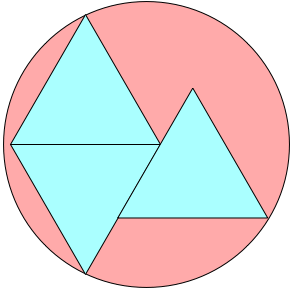 s = (√3+√2)/3 = 1.048+ | n=1 s = 1.151+ Jeremy Galvagni |
n=0, 1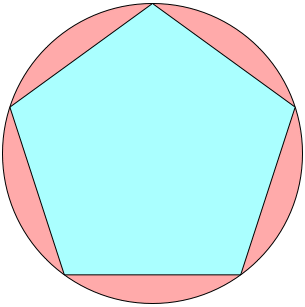 s = 1.175+ | n=2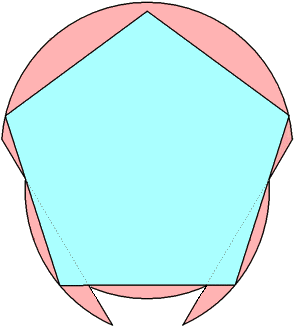 s = 1.203+ Jeremy Galvagni |
n=0, 1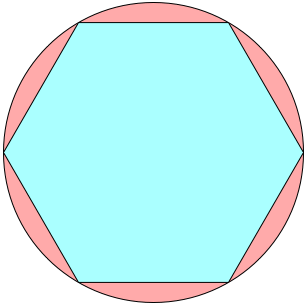 s = 1 | n=2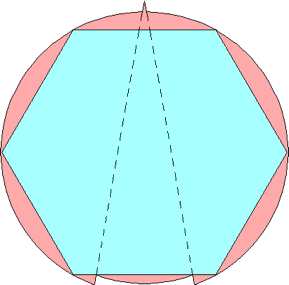 s = 1.007+ Maurizio Morandi | n=3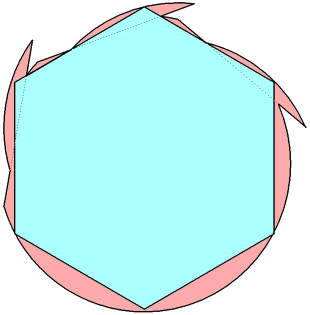 s = 1.018+ Jeremy Galvagni |
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 11/19/17.