Problem of the Month (November 2018)

Skyline is a computer game similar to Tetris. A computer generates squares or triangles randomly, with equal probability. These can be placed on top of something until the next piece does not fit anywhere. Squares can only be placed on a horizontal surface, directly on top of another square or an upside-down triangle. Triangles can be placed right-side-up on a horizontal surface, or upside-down supported on each side by two other triangles. We are interested in computing the average number of moves that can be made in different types of positions. For example, here are some small positions:

In this position, if we call the average number of movies remaining E, half the time we get a square leaving the same situation with 1 more move, and half the time we get a triangle that we can place but would end the game. Thus E = ½(E+1) + ½(1), or E=2.

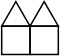In this position, half the time we get a square which ends the game immediately, and half the time we get a triangle that we can place upside-down to leave the previous example. Thus E = ½(0) + ½(1+2), or E=3/2.

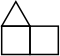In this position, half the time we get a square which leads to our first example, and half the time we get a triangle that leads to our second example. Thus E = ½(2+1) + ½(3/2+1), or E=11/4.

Can you find how long the game will last on average from the positions below, which are enough to completely solve the width 2 cases? How about positions of width 3? Warning: some of them are tricky because it is unclear what the best placement of a piece is. And there are infinite chains you will have to deal with for seemingly simple positions.

   

ANSWERS

Joe DeVincentis sent the correct answers to the width 2 cases, which are shown below.

end
↑

3/2=1.5		←
11/4=2.75		←
37/8=4.625
↓ ↙↑ ↕

2
19/8=2.375		←
9/2=4.5
↺↘ ↓

0

Here are the solutions for expected lifetimes for width 3 positions. Evert Stenlund corrected some of my calculations. Then in 2021, Rohan Ridenour found some improvements.

↑ ↑ ↑

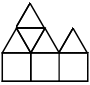15/8=1.875+ (RR) 		←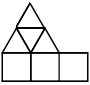
47/16=2.937+ (RR) 		←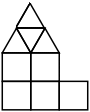
79/32=2.468+ (RR) 		←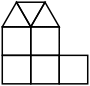
3703.576=6.428+ (RR) 		←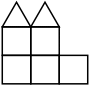
295/36=8.194+ (ES) 		←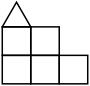
463/48=9.645+ (ES)
↙ ↙ ↙ ↖
←
13/2=6.5 		←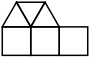
151/18=8.388+ 		←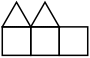
295/36=8.194+ 		←
655/72=9.097+ 		←
10949/1008=10.862+ (ES) 		←
709/63=11.253+ (ES)
↓ ↓ ↓ ↓ ↓ ↗
←
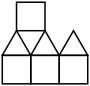51/8=6.375 		←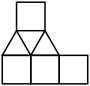
149/18=8.277+
6 		←
8 		←
1339/126=10.626+ (ES)
↓ ↓ ↺ ↘↺
these lead to a collection of towers where squares are
put on the left and triangles are put on the right
2 		←
4

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 11/23/18.