Problem of the Month (November 1999)

This month's problem comes from graph theory. A graph is a collection of points (vertices) and lines between points (edges). The complete graph K_n is the graph with n vertices with an edge between every two vertices.

Paul Erdös, famous for offering cash awards for unsolved problems, offered $100 for the solution of the following problem:

Let f(c,a,b) denote the smallest integer n for which there is a graph G with n vertices with the properties that: 1) any edge coloring in c colors contains a monochromatic copy of K_a, and 2) G contains no K_b. Prove or disprove f(2,3,4) < 10⁶.

The best known upper bound is f(2,3,4) < 3x10⁹. This problem is really hard, so here is a variation. What if you colored the vertices instead of the edges? Define f(c,a,b) the same way.

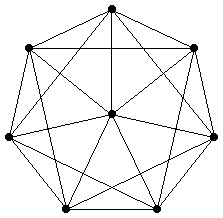
For example, the graph below shows that f(2,3,5) ≤ 8. Do you see why?

What bounds can you get on f(c,a,b)? Are all the values of f(c,a,b) finite?

ANSWERS

There were no responses this month. Here are my best upper bounds:

Upper Bounds for f(2,a,b)

a \ b	2	3	4	5	6	7	8
1	1	1	1	1	1	1	1
2	-	5	3	3	3	3	3
3	-	-	15	8	5	5	5
4	-	-	-	?	45	15	7

Upper Bounds for f(3,a,b)

a \ b	2	3	4	5	6	7	8
1	1	1	1	1	1	1	1
2	-	14	7	4	4	4	4
3	-	-	?	?	45	17	7

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 11/25/99.