Problem of the Month (December 2006)

This month we investigate triangulating polygons. If a regular polygon P with k sides can be cut into n triangles with sides no larger than 1, what is the largest value of the side length s of P? What are the best solutions for small values of k and n?

ANSWERS

Gavin Theobald and Trevor Green filled in some gaps on a problem on which they have sent many solutions over the years.

The best known solutions are shown below.

Triangulations of a Triangle
n=1

s = 1
n=4

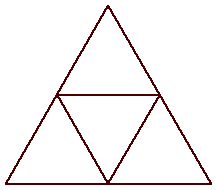
s = 2
n=8

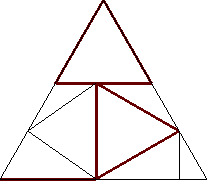
s = 1 + 2 / √3 = 2.154+
(Gavin Theobald) n=9

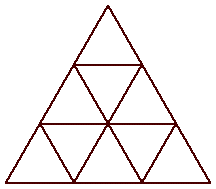
s = 3

n=13

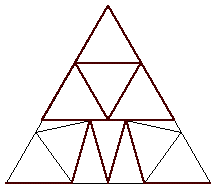
s = 2 + 4/√13 = 3.109+
(Trevor Green) n=14

2 + 2/√3 = 3.154+
n=15

s = s = √3 + 3/2 = 3.232+
n=16

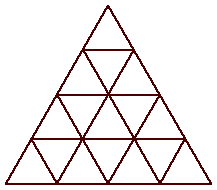
s = 4

n=20

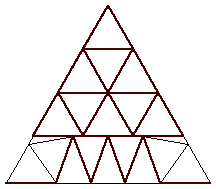
s = (3√109 + 83) / 28 = 4.082+
(Trevor Green) n=21

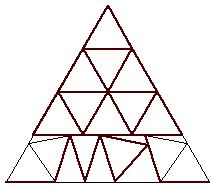
s = 4.102+
(Trevor Green) n=22

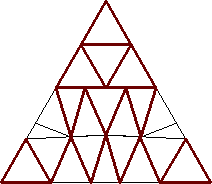
s = 4.161+
(Trevor Green) n=23

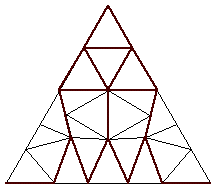
s = 4.205+

n=24

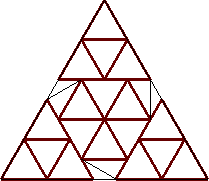
s = 9/2 = 4.500
(Trevor Green) n=25

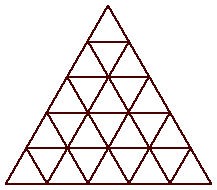
s = 5

Triangulations of a Square
n=2

s = 1 / √2 = .707+ n=3

s = 2 / √5 = .894+ n=4

s = 1 n=7

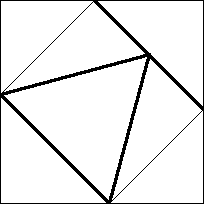
s = 1 / √2 + √(3/8) = 1.319+
n=8

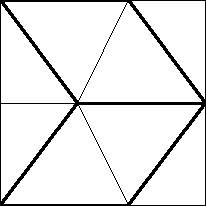
s = 8 / 5 = 1.600
n=9

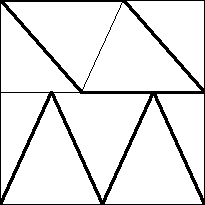
s = 1.660+
n=10

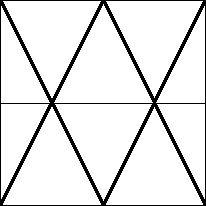
s = 4 / √5 = 1.788+
n=11

s = (1+√7) / 2 = 1.822+
(Gavin Theobald)
n=12

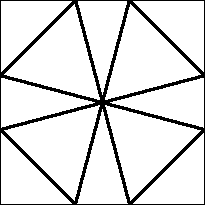
s = 1 / √(2) + √(3/2) = 1.931+
n=13

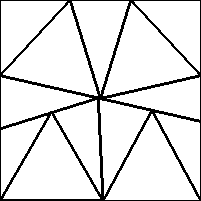
s = 1.949+
(Gavin Theobald) n=14

s = 2
n=15

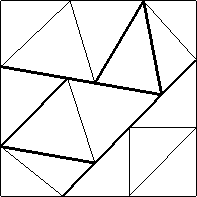
s = 2.044+
(Gavin Theobald)
n=16

s = 2.247+
(Gavin Theobald) n=17

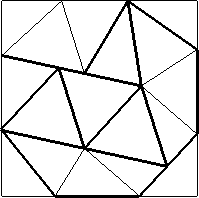
s = 2.308+
(Gavin Theobald) n=18

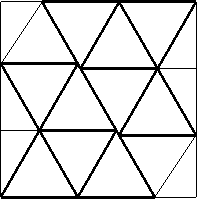
s = 6 - 2√3 = 2.535+
(Gavin Theobald) n=19

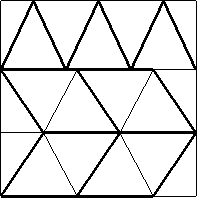
s = 2.560+
(Gavin Theobald)
n=20

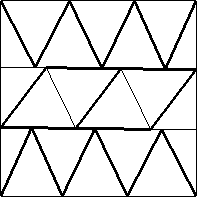
s = 2.604+
(Gavin Theobald) n=21

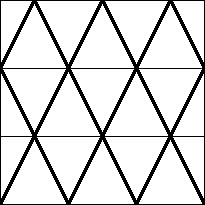
s = 6 / √5 = 2.683+
n=22

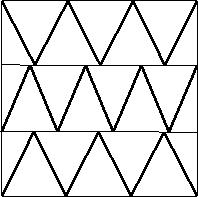
s = 2.707+
(Gavin Theobald) n=23

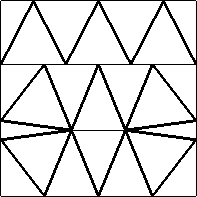
s = 2.740+
(Gavin Theobald)
n=24

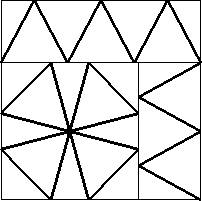
s = 2.811+
(Gavin Theobald) n=25

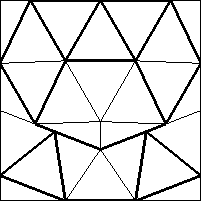
s = 2.864+
(Gavin Theobald) n=26

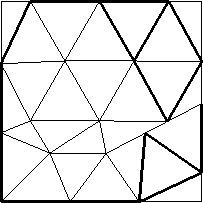
s = 2.905+
(Gavin Theobald) n=27

s = 3

Triangulations of a Pentagon
n=3

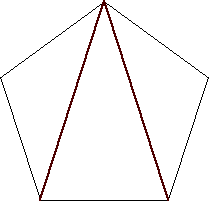
s = (√5 - 1) / 2 = .618+
n=4

s = 2 / √(5 + 2√5) = .649+
n=5

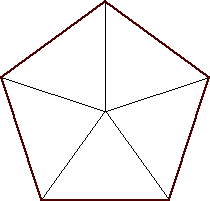
s = 1
n=10

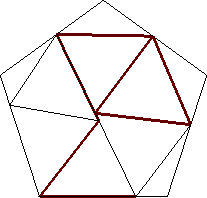
s = 1.326+
(Gavin Theobald)
n=11

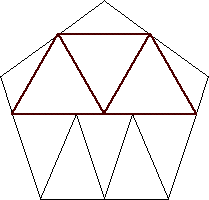
s = 1.399+
(Trevor Green) n=12

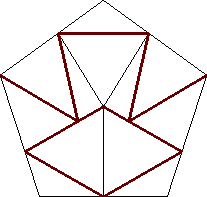
s = 1.411+
(Trevor Green) n=13

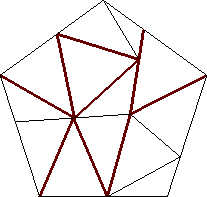
s = 1.489+
(Gavin Theobald) n=14

s = 1.595+
(Gavin Theobald)
n=15

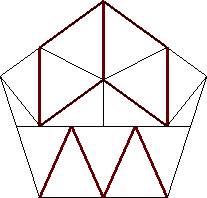
s = 1.625+
(Gavin Theobald) n=16

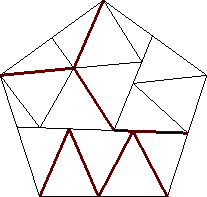
s = 1.723+
(Gavin Theobald) n=17

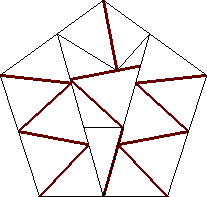
s = 1.784+
(Gavin Theobald) n=18

s = 1.922+
(Gavin Theobald)
n=19

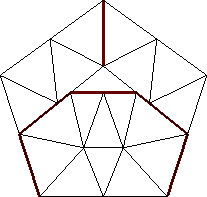
s = 1.938+
(Gavin Theobald) n=20

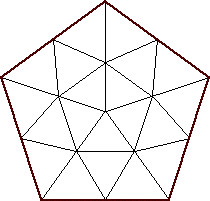
s = 2

Triangulations of a Hexagon
n=4

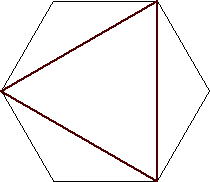
s = 1 / √3 = .577+
n=6

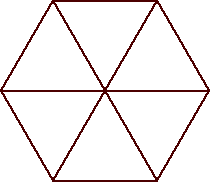
s = 1
n=12

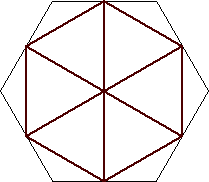
s = 2 / √3 = 1.154+
n=15

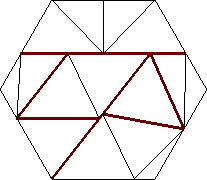
s = 1.251+
(Gavin Theobald)
n=16

s = 1.390+
(Gavin Theobald) n=18

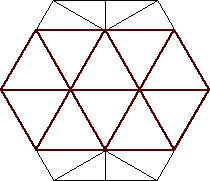
s = 3/2 = 1.500
n=19

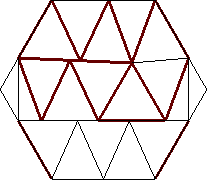
s = 1.541+
(Gavin Theobald) n=20

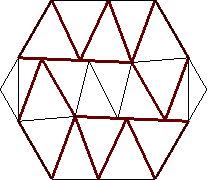
s = 1.549+
(Gavin Theobald)
n=21

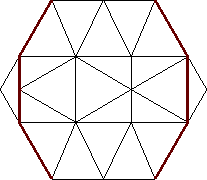
s = 1 + 1 / √3 = 1.577+
(Gavin Theobald) n=22

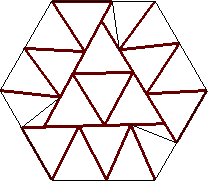
s = 1.709+
(Gavin Theobald) n=24

s = 2

Triangulations of a Heptagon
n=5

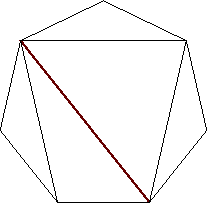
s = .445+
(Trevor Green) n=6

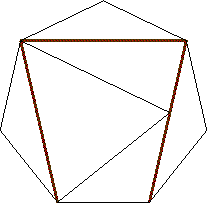
s = .554
(Trevor Green) n=7

s = .867+
(Trevor Green) n=10

s = .890
(Gavin Theobald)
n=11

s = .985+
(Gavin Theobald) n=12

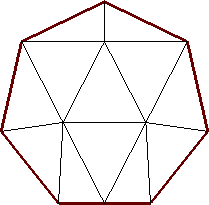
s = 1
(Trevor Green) n=17

s = 1.031+
(Gavin Theobald) n=18

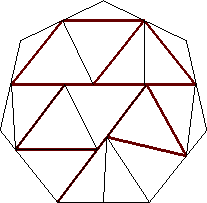
s = 1.124+
(Gavin Theobald)

Triangulations of a Octagon
n=6

s = √2 - 1 = .414+
(Trevor Green) n=7

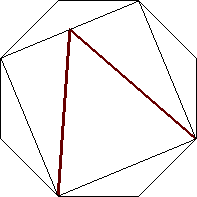
s = .484+
(Gavin Theobald) n=8

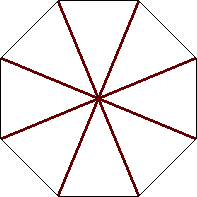
s = .765+
(Trevor Green) n=11

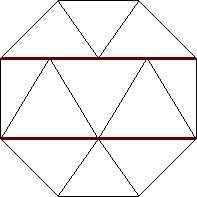
s = 2√2 - 2 = .828+
(Gavin Theobald)
n=12

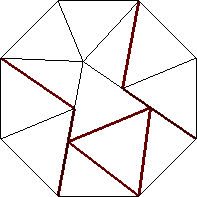
s = .907+
(Gavin Theobald) n=13

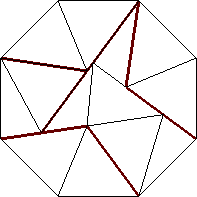
s = .927+
(Gavin Theobald) n=14

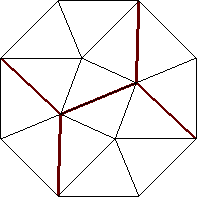
s = .986+
(Gavin Theobald) n=15

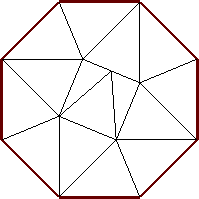
s = 1
(Gavin Theobald)
n=22

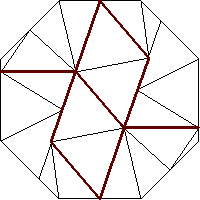
s = 1.097+
(Trevor Green)

Trevor Green also sent an analysis of small triangulations of polygons with more than 6 sides. Among his results:

The optimal (n–2)-triangulation of a 3k-gon has s = 2 sin(π/n) / √3.
The optimal (n–2)-triangulation of a (3k+1)-gon has s = sin(π/n) / sin(π(n+2)/3n).
The optimal (n–2)-triangulation of a (3k+2)-gon has s = sin(π/n) / sin(π(n+1)/3n).

The optimal (n–1)-triangulation of a 5-gon or (3k+1)-gon can be improved slightly.

The optimal n-triangulation of an n-gon has s = 2 sin(π/n).

The optimal (n+3)-triangulation of an n-gon cannot be improved.

The optimal (n+4)-triangulation of a 3k-gon has s = 4 sin(π/n) / √3.
The optimal (n+4)-triangulation of a (3k+1)-gon has s = 2 sin(π/n) / sin(π(n+2)/3n).
The optimal (n+4)-triangulation of a (3k+2)-gon has s = 2 sin(π/n) / sin(π(n+1)/3n).

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 2/24/11.