 |  |
Any graph whose vertices have degrees 10 or less can be labeled: label each vertex with 9 times its degree. We therefore consider these labelings trivial and omit them below. In fact, Joe DeVincentis pointed out this is true as long as all the degrees d of the graph have the property that 9d has digit sum 9.
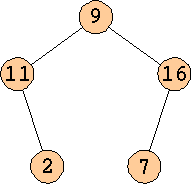
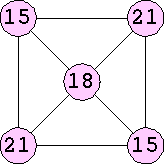
Here are some of the small digit sum graphs:
| Length | Labelings |
|---|---|
| 2 | 1, 1 2, 2 3, 3 4, 4 5, 5 6, 6 7, 7 8, 8 |
| 5 | 1, 10, 9, 17, 8 2, 11, 9, 16, 7 3, 12, 9, 15, 6 4, 13, 9, 14, 5 |
| 8 | 1, 10, 9, 17, 17, 9, 10, 1 2, 11, 9, 16, 16, 9, 11, 2 3, 12, 9, 15, 15, 9, 12, 2 4, 13, 9, 14, 14, 9, 13, 4 5, 14, 9, 13, 13, 9, 14, 5 6, 15, 9, 12, 12, 9, 15, 6 7, 16, 9, 11, 11, 9, 16, 7 8, 17, 9, 10, 10, 9, 17, 8 8, 17, 18, 19, 19, 18, 17, 8 |
In 2011, the Marin Math Circle discovered that these patterns likely continue. Only for n = 2 (mod 3) are there solutions, and these solutions are symmetric for even n and asymmetric for odd n.
| Length | Labelings |
|---|---|
| 4 | 6, 12, 6, 12 |
| 6 | 2, 10, 8, 16, 8, 10 3, 10, 7, 15, 8, 11 4, 10, 6, 14, 8, 12 4, 11, 7, 14, 7, 11 5, 10, 5, 13, 8, 13 5, 11, 6, 13, 7, 12 6, 12, 6, 12, 6, 12 9, 10, 10, 9, 17, 17 9, 11, 11, 9, 16, 16 9, 12, 12, 9, 15, 15 9, 13, 13, 9, 14, 14 17, 17, 18, 19, 19, 18 |
| 8 | 6, 12, 6, 12, 6, 12, 6, 12 |
| 10 | 6, 12, 6, 12, 6, 12, 6, 12, 6, 12 |
| Degree | Labelings |
|---|---|
| 1 | 1 2 3 4 5 6 7 8 |
| 4 | 12 24 48 |
| 7 | 21 (Ed Pegg) 42 (Ed Pegg) 84 (Ed Pegg) |
| 10 | 10 (JD) 20 (JD) 30 (JD) 40 (JD) 50 (JD) 60 (JD) 70 (JD) 80 (JD) |
| 11 | 198 (JD) |
| 13 | 195 (JD) |
| 16 | 192 (JD) 288 (JD) |
| 19 | 114 (JD) 133 (JD) 152 (JD) 190 (JD) 209 (JD) 228 (JD) 247 (JD) 266 (JD) 285 (JD) |
| 21 | 378 (JD) |
| 22 | 132 (JD) |
| m \ n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1, 1 2, 2 3, 3 4, 4 5, 5 6, 6 7, 7 8, 8 | ||||||||
| 2 | 6, 12 | ||||||||
| 3 | |||||||||
| 4 | 3, 12 6, 24 | 12, 12 24, 24 48, 48 | |||||||
| 5 | 2, 10 4, 20 6, 30 8, 40 10, 5 12, 15 14, 25 16, 35 | 15, 30 | |||||||
| 6 | |||||||||
| 7 | 3, 21 6, 42 | 12, 21 20, 14 24, 42 28, 70 32, 35 40, 28 44, 56 48, 84 52, 49 56, 77 68, 98 | 21, 21 42, 42 84, 84 | ||||||
| 8 | 12, 24 24, 48 | 30, 24 60, 48 75, 96 | 32, 40 64, 80 88, 128 | ||||||
| 9 | |||||||||
| 10 | 1, 10 2, 20 3, 30 4, 40 5, 50 6, 60 7, 70 8, 80 | 12, 30 24, 60 | 21, 30 42, 60 | ||||||
| 11 | 18, 99 (JD) | 12, 33 24, 66 36, 99 | 54, 99 | 72, 99 | 10, 11 20, 22 30, 33 40, 44 50, 55 60, 66 70, 77 80, 88 90, 99 | 108, 99 | 126, 99 | 144, 99 48, 132 96, 165 | 162, 99 |
1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8
1 10 9 17 8 2 11 9 16 7 3 12 9 15 6 4 13 9 14 5
1 10 9 17 17 9 10 1 2 11 9 16 16 9 11 2
3 12 9 15 15 9 12 3 4 13 9 14 14 9 13 4
5 14 9 13 13 9 14 5 6 15 9 12 12 9 15 6
7 16 9 11 11 9 16 7 8 17 9 10 10 9 17 8
8 17 18 19 19 18 17 8
10 18 26 18 10 11 18 25 18 11 12 18 24 18 12 10 18 26 18 10 11 18 25 18 11 12 18 24 18 12
13 18 23 18 13 14 18 22 18 14 15 18 21 18 15 13 18 23 18 13 14 18 22 18 14 15 18 21 18 15
16 18 20 18 16 16 27 29 27 16 17 27 28 27 17 16 18 20 18 16 16 27 29 27 16 17 27 28 27 17
19 27 26 27 19 19 27 26 27 19
10 14 14 10 12 15 15 12 14 16 16 14 14 26 26 14 15 24 24 15 16 22 22 16 14 26 26 14 15 24 24 15 16 22 22 16 10 14 14 10 12 15 15 12 14 16 16 14
16 17 17 16 16 26 26 16 20 19 19 20 17 20 20 17 26 38 38 26 19 34 34 19 17 20 20 17 26 38 38 26 19 34 34 19 16 17 17 16 16 26 26 16 20 19 19 20 |
| Size | Center | Other Labelings |
|---|---|---|
| 5 | 18 | 15, 21, 15, 21 |
| 6 | 15 | 12, 12, 12, 12, 12 |
| 30 | 15, 15, 15, 15, 15 | |
| 7 | 27 | 13, 20, 16, 23, 16, 20 |
| 14, 20, 15, 22, 16, 21 | ||
| 15, 21, 15, 21, 15, 21 | ||
| 36 | 17, 20, 21, 19, 25, 24 | |
| 17, 21, 22, 19, 24, 23 | ||
| 17, 22, 23, 19, 23, 22 | ||
| 18, 20, 20, 18, 25, 25 | ||
| 18, 21, 21, 18, 24, 24 | ||
| 18, 22, 22, 18, 23, 23 | ||
| 54 | 25, 25, 27, 29, 29, 27 | |
| 25, 26, 28, 29, 28, 26 | ||
| 26, 26, 27, 28, 28, 27 | ||
| 9 | 8 | 10, 10, 10, 10, 10, 10, 10, 10 |
| 16 | 11, 11, 11, 11, 11, 11, 11, 11 | |
| 20 | 4, 10, 4, 10, 4 10, 4, 10 | |
| 24 | 12, 12, 12, 12, 12, 12, 12, 12 | |
| 28 | 14, 20, 14, 20, 14, 20, 14, 20 | |
| 32 | 13, 13, 13, 13, 13, 13, 13, 13 | |
| 36 | 15, 21, 15, 21, 15, 21, 15, 21 | |
| 40 | 8, 20, 8, 20, 8, 20, 8, 20 | |
| 14, 14, 14, 14, 14, 14, 14, 14 | ||
| 44 | 16, 22, 16, 22, 16, 22, 16, 22 | |
| 48 | 18, 30, 18, 30, 18, 30, 18, 30 | |
| 24, 24, 24, 24, 24, 24, 24, 24 | ||
| 52 | 17, 23, 17, 23, 17, 23, 17, 23 | |
| 56 | 25, 25, 25, 25, 25, 25, 25, 25 | |
| 60 | 18, 24, 18, 24, 18, 24, 18, 24 | |
| 64 | 26, 26, 26, 26, 26, 26, 26, 26 | |
| 80 | 28, 28, 28, 28, 28, 28, 28, 28 | |
| 11 | 45 | 15, 21, 15, 21, 15, 21, 15, 21, 15, 21 |
| 12 | 33 | 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12 (JD) |
Bryce Herdt suggested investigating the smallest graph to have label n. He found that K11 has a labeling including 100, and K7 has a labeling including 108. It turns out this problem is fairly easy for all n with digit sum 9 or less. Connect n to its digital sum s and several copies of 9, each of which is connected connected to the same copy of (18–s), which in turn is connected to (9–s). If n has digit sum between 9 and 18, then connect n to s and a bunch of copies of 18, each of which is connected to (27–s), which in turn is connected to (18–s).
Bryce Herdt also suggested investigating the smallest graph whose labels are the first n positive integers, or in different bases, or both! He gave an example in base 2:
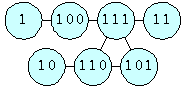
Bryce Herdt also suggested investigating the smallest graph (besides P2) whose labels have greatest common divisor n.
|
|
Joe DeVincentis wondered whether ALL graphs have these digit sum labelings.
If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 3/3/11.