Problem of the Month (December 2011)

Given a planar graph with no endpoints, what are the smallest non-negative labels the vertices can have so that all the inherited edge labels (which are the sum of the labels of the two vertices they connect) are different squares?

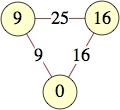
Here smallest means minimal total, and among those, minimal maximum vertex label.

ANSWERS

Below are some graphs with 9 or fewer edges, and the smallest known vertex labelings. Can you improve any of these? Can you find any graphs I missed?

3 Edges

4 Edges

5 Edges

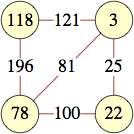(Andrew Bayly)

6 Edges

(Jon Palin)

7 Edges

8 Edges



		(Jon Palin)

9 Edges







(Jon Palin)	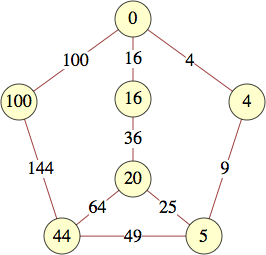(George Sicherman)	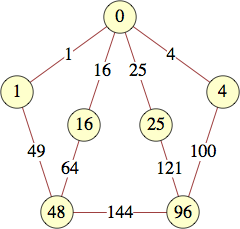(George Sicherman)
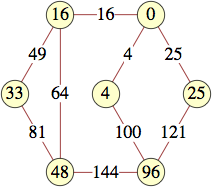(George Sicherman)	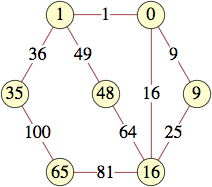(George Sicherman)	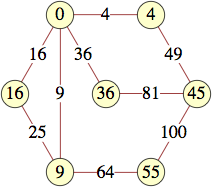(George Sicherman)

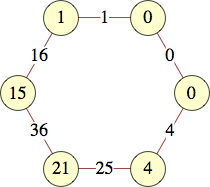
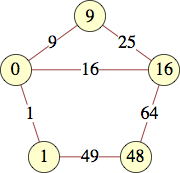
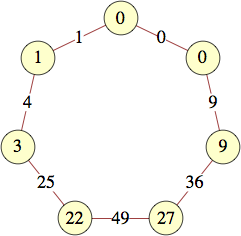
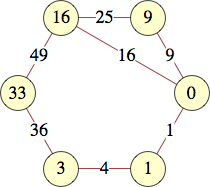
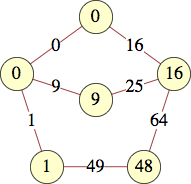
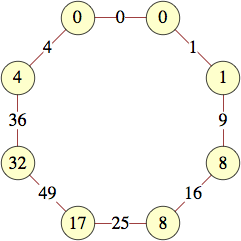
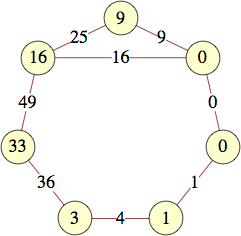
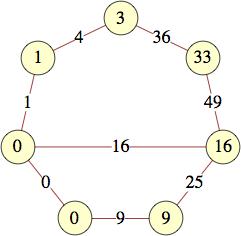
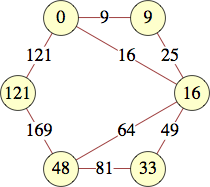
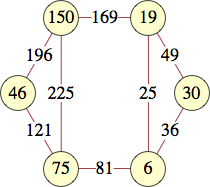
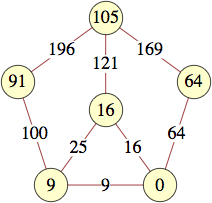
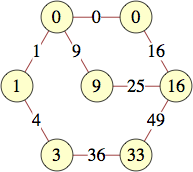
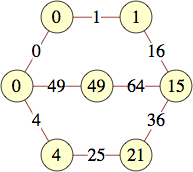
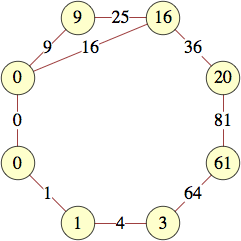
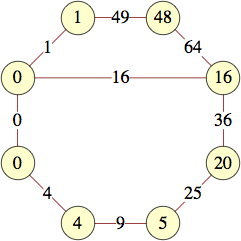
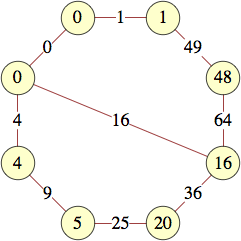
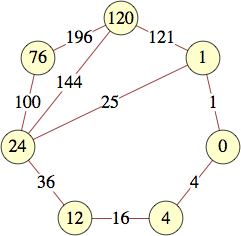
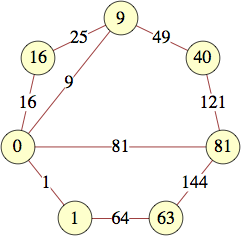
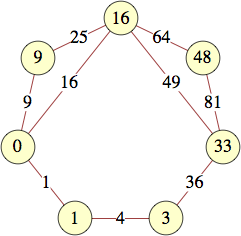
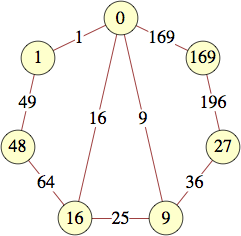
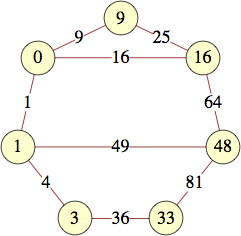
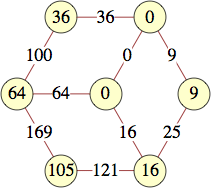
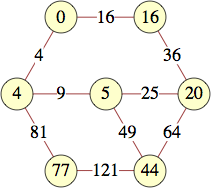
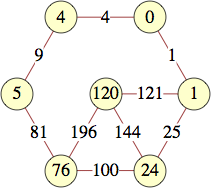
The smallest labels for cycles with n vertices are shown below:

Smallest Cycle Graphs with n Vertices

n	labels	author
3	0, 9, 16
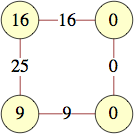
4	0, 0, 9, 16
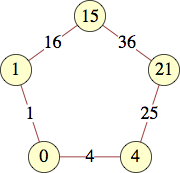
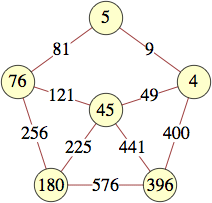
5	0, 1, 15, 21, 4	Andrew Bayly
6	0, 0, 1, 15, 21, 4
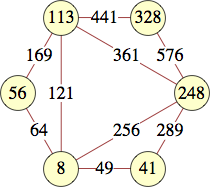
7	0, 0, 1, 3, 22, 27, 9
8	0, 0, 1, 8, 8, 17, 32, 4
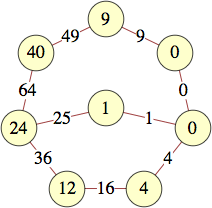
9	0, 0, 1, 8, 8, 17, 32, 32, 4	George Sicherman
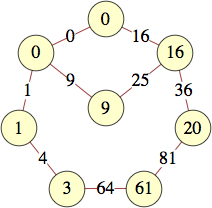
10	0, 0, 1, 8, 28, 21, 60, 61, 39, 25	George Sicherman
11	0, 0, 1, 8, 8, 28, 21, 60, 61, 39, 25	George Sicherman
12	0, 0, 1, 3, 6, 43, 38, 62, 59, 5, 11, 25	George Sicherman
13	0, 0, 1, 3, 6, 10, 39, 61, 3, 22, 59, 85, 36	George Sicherman
14	0, 0, 1, 3, 13, 51, 49, 32, 4, 5, 20, 101, 95, 49	George Sicherman
15	0, 0, 1, 3, 6, 10, 26, 38, 11, 14, 67, 33, 88, 56, 169	George Sicherman
16	0, 0, 1, 3, 6, 10, 111, 58, 6, 19, 17, 83, 113, 112, 32, 49	Alex Rower
17	0, 0, 1, 3, 6, 10, 26, 55, 9, 16, 128, 128, 41, 8, 92, 104, 121	Alex Rower
18	0, 0, 1, 3, 6, 10, 15, 34, 2, 62, 19, 81, 63, 162, 162, 34, 135, 121	Alex Rower

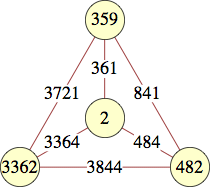
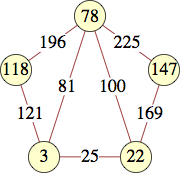
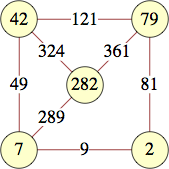
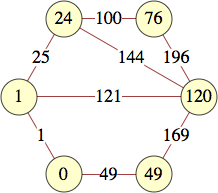
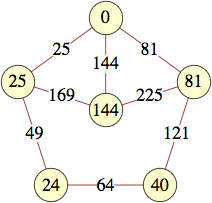
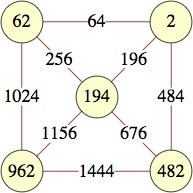
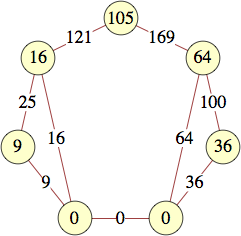
The smallest labels for wheels with n vertices are shown below:

Smallest Wheel Graphs with n Vertices

n	center	others	author
4	2	3362, 359, 482	Jon Palin
5	194	962, 62, 2, 482	Jon Palin
6	224	1712, 137, 32, 452, 2912	Jon Palin
7	144	3456, 25, 0, 256, 585, 640	Jon Palin
8	144	880, 81, 0, 256, 585, 5040, 7956	Jon Palin
9	260	701, 140, 29, 1340, 2141, 6140, 101, 524	Jon Palin
10	482	962, 194, 2, 47, 1634, 1282, 9122, 3874, 887	Jon Palin
11	212	364, 77, 44, 317, 2492, 1997, 1724, 877, 3884, 1157	Jon Palin
12	8	136, 188, 1928, 281, 248, 3473, 1288, 5768, 161, 568, 953	George Sicherman

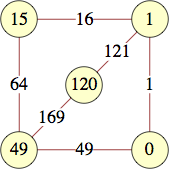
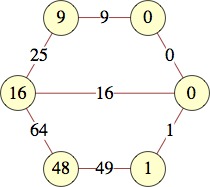
The smallest labels for n-dimensional cubes are shown below:

Smallest n-Dimensional Cube Graphs

n	labels	author
2	0, 0, 9, 16
3	0, 0, 9, 16, 153, 72, 49, 576	George Sicherman

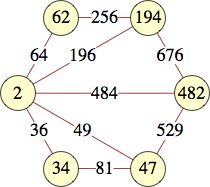
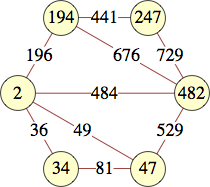
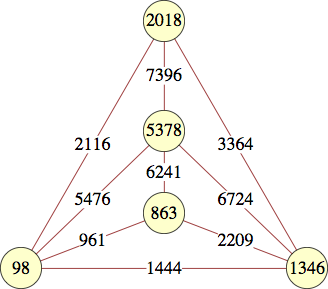
The smallest labels for complete graphs on n vertices are shown below:

Smallest Complete Graphs with n Vertices

n	labels	author
3	0, 9, 16
4	2, 359, 482, 3362	Jon Palin
5	7442, 28658, 148583, 177458, 763442	Jean-Louis Nicolas

In 2019, Alex Rower found these grid graphs, prism graphs, and complete bipartite graphs:

Smallest m×n Grid Graphs

m \ n	2	3	4	5
2	0 0 9 16
3	0 9 0 16 1 48	15 1 224 49 0 100 32 4 21
4	0 9 0 16 1 48 3 33	15 1 360 49 0 169 72 9 27 184 216 73	96 48 1 224 345 16 0 100 280 9 0 576 681 160 36 448
5	3 33 1 48 0 16 0 9 121 135	1 24 552 168 57 232 561 64 297 400 0 144 84 16 180	0 1296 385 291 0 225 99 70 121 504 1345 1155 75 25 24 1 825 264 760 840	0 0 1 24 1201 576 49 120 76 824 385 15 241 600 2425 1215 1921 288 1081 75 306 783 1 2400 409

Smallest Prism Graphs

n	labels
3	12 52 69 157 204 372
4	0 0 9 16 576 49 72 153
5	0 4 12 13 36 324 252 109 516 160
6	0 4 96 48 33 16 64 152 433 528 256 105

Smallest m,n Bipartite Graphs

m \ n	2	3	4	5
2	0, 9 0, 16
3	1, 49 0, 15, 120	0, 273, 768 16, 256, 1936
4	0, 144 0, 25, 81, 256	1, 961, 6241 0, 483, 1155, 13923	0, 906304, 3240000, 12503296 0, 921600, 3186225, 43956900
5	9, 729 0, 55, 112, 567, 952	9, 8649, 56169 0, 4347, 10395, 42427, 125307	?	?

Alex Rower found the 2,5, 3,5 and 4,4 bipartite graphs above, and cycle and grid graphs for triangular, pentagonal, hexagonal, and octagonal numbers.

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 6/25/23.