Problem of the Month
(December 2013)

This month we pack squares and regular octagons in each other. What is the smallest square that contains non-overlapping octagons with sides 1-n? We can ask the same question about squares in octagons, and octagons in octagons.

ANSWERS

Here are the best known results:
Octagons In Squares

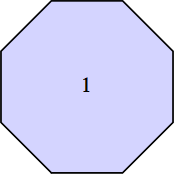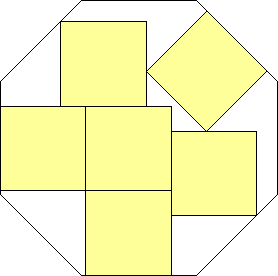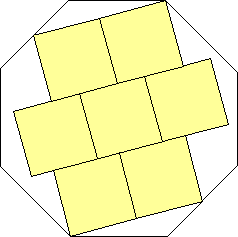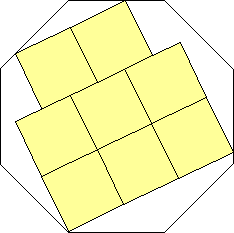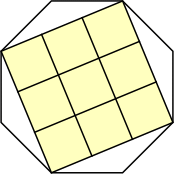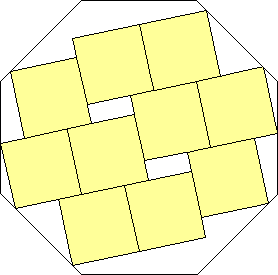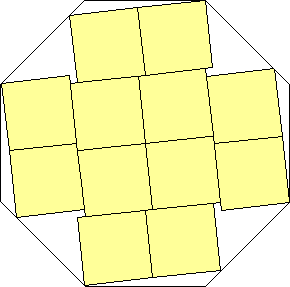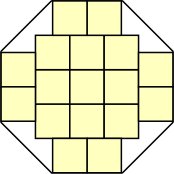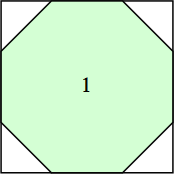
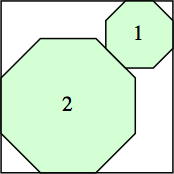
s = 1 + √2
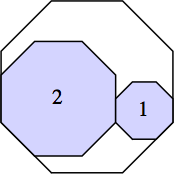
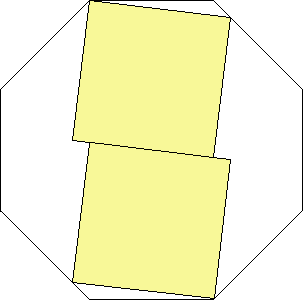
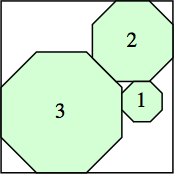
s = 3 + (9/4) √2
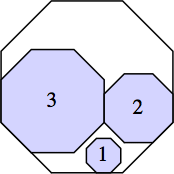
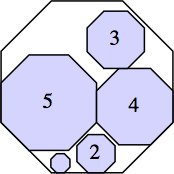
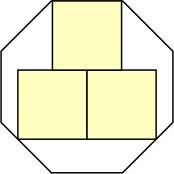
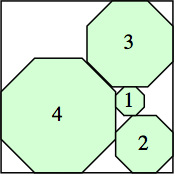
s = 5 + (15/4) √2
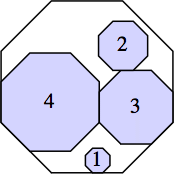
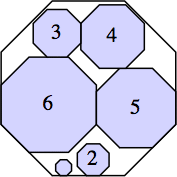
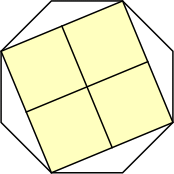
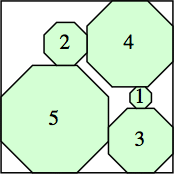
s = 6 (1 + √2)
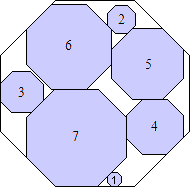
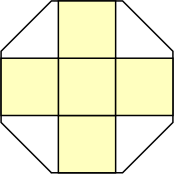
s = 8 (1 + √2)
 

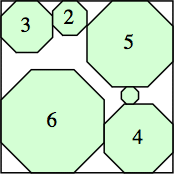
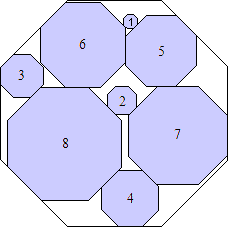
s = 10 (1 + √2)
 
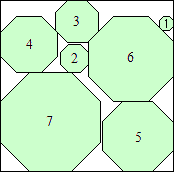
s = (41 + 33√2)/3
(Maurizio Morandi)
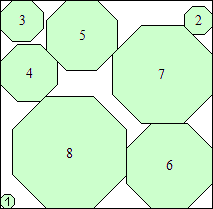
s = (138 + 105√2)/8
(Maurizio Morandi)
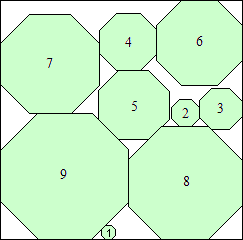
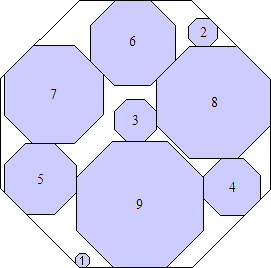
s = 17(1 + √2)
(Maurizio Morandi)
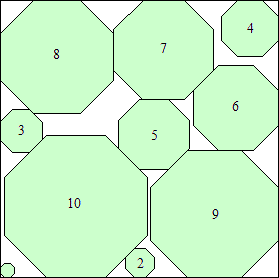
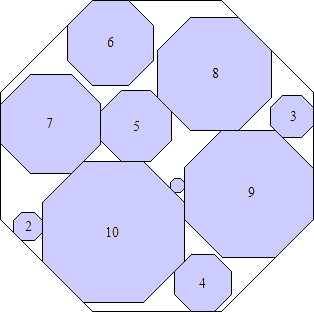
s = (137 + 104√2)/6
(Maurizio Morandi)

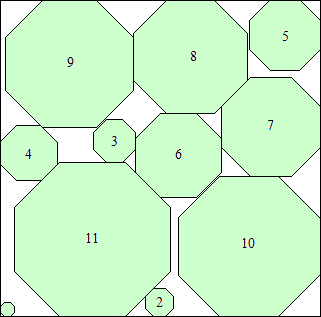
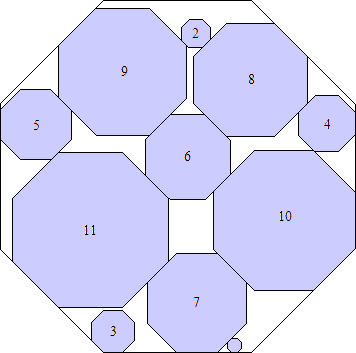
s = 26 + 20√2
(Maurizio Morandi)
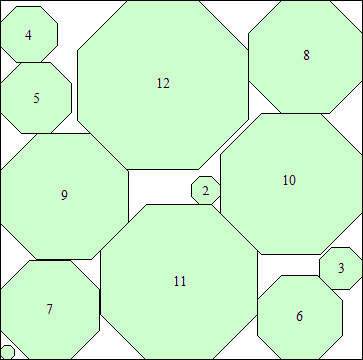
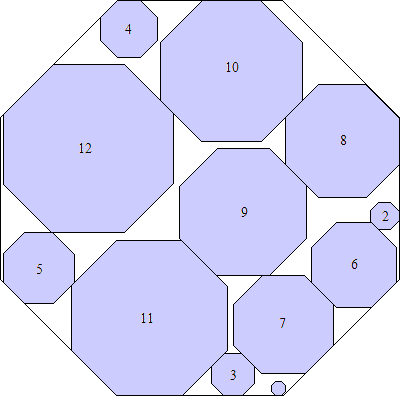
s = (120 + 89√2)/4
(Maurizio Morandi)
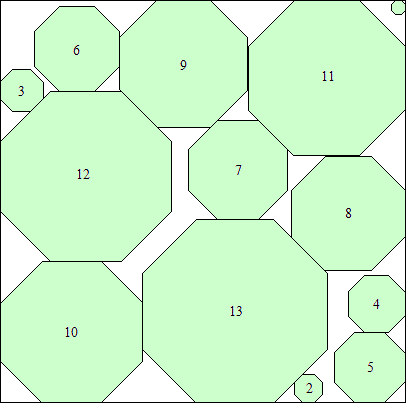
s = (260 + 205√2)/8
(Maurizio Morandi)
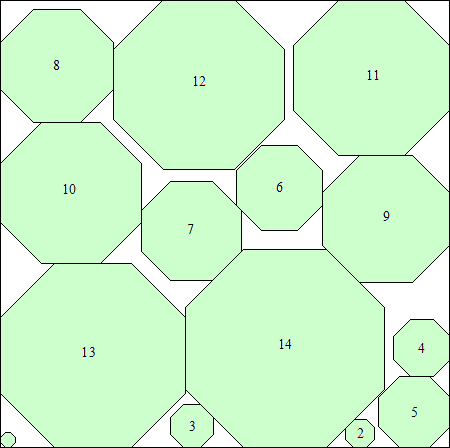
s = (140 + 117√2)/4
(Maurizio Morandi)
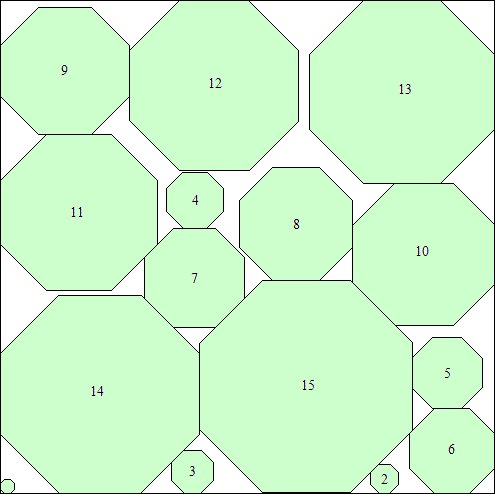
s = (118 + 95√2)/3
(Maurizio Morandi)

Octagons In Octagons

s = 1
s = 3
s = 5
s = 7
s = 9
 

s = 11
 
s = 11(1 + √2)/2
(Maurizio Morandi)
s = (38 + 7√2)/3
(Maurizio Morandi)
s = (123 + 141√2)/17
(Maurizio Morandi)
s = 31 / √2
(Maurizio Morandi)

s = 25
(Maurizio Morandi)
s = 4 + 17√2
(Maurizio Morandi)
s = (115 + 294√2)/17
(Maurizio Morandi)
s = (359 + 164√2)/17
(Maurizio Morandi)
s = (151 + 83√2)/7
(Maurizio Morandi)

Squares In Octagons

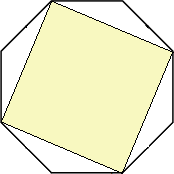
s = 1 / √(2+√2)
(Andrew Bayly)
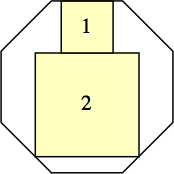
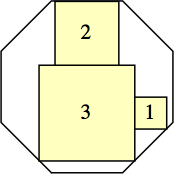
s = 24 – 16√2
 
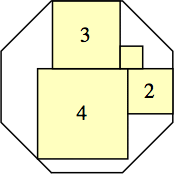
s = 39 – 26√2
 
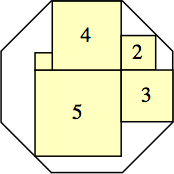
s = 13 (3√2 – 4)
(Maurizio Morandi)
s = 17 (3√2 – 4)
(Maurizio Morandi)

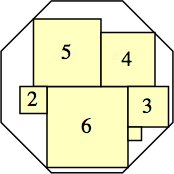
s = 18 – 9√2
 
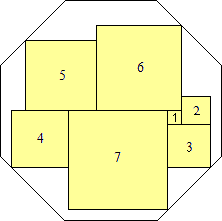
s = 11(2 – √2)
(Maurizio Morandi)
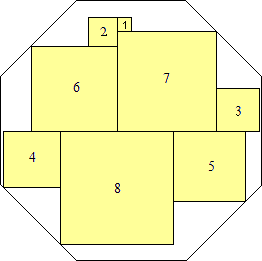
s = 13(2 – √2)
(Maurizio Morandi)
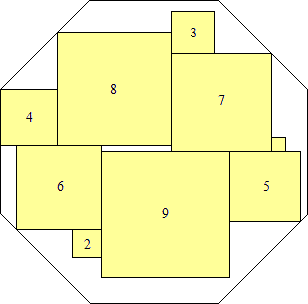
s = 61(2 – √2)/4
(Maurizio Morandi)
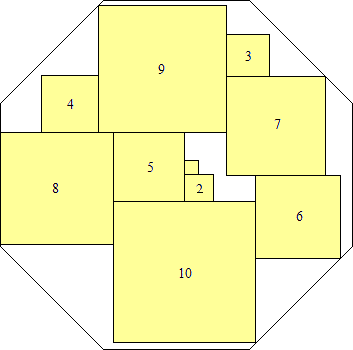
s = 95(5 – 3√2)/7
(Maurizio Morandi)

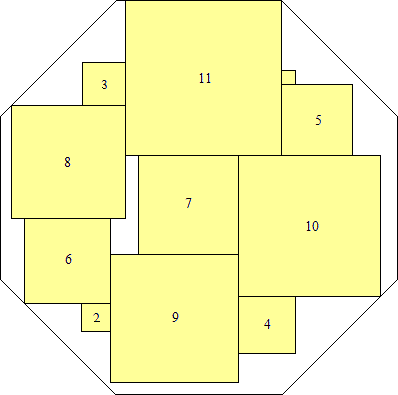
s = 79(2 – √2)/4
(Maurizio Morandi)
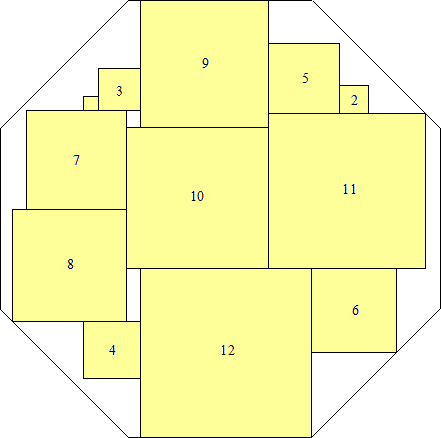
s = 31(√2 – 1)
(Maurizio Morandi)
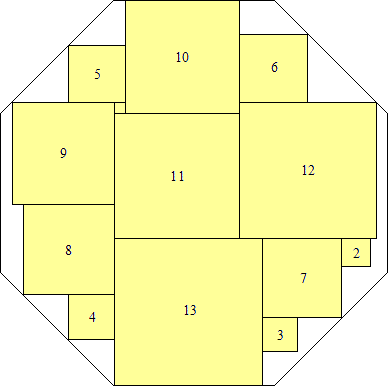
s = 34(√2 – 1)
(Maurizio Morandi)
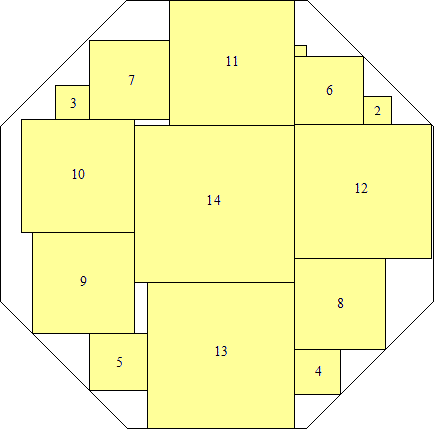
s = 38(√2 – 1)
(Maurizio Morandi)
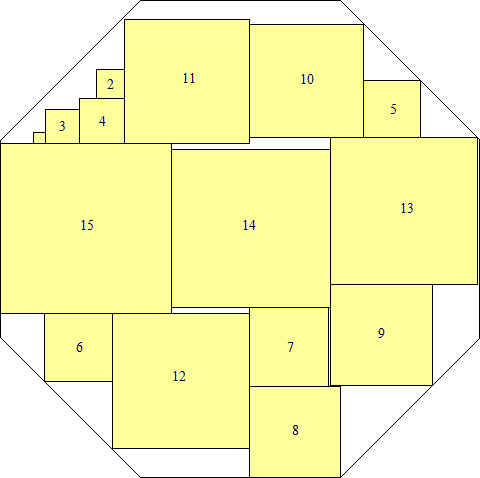
s = 102(3 – 2√2)
(Maurizio Morandi)

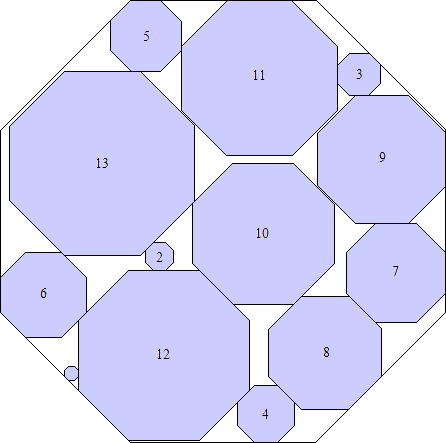
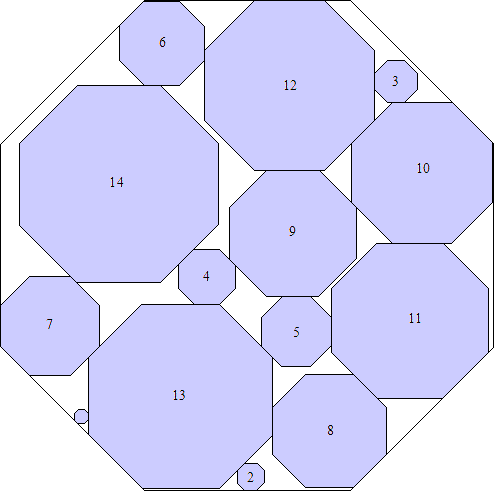
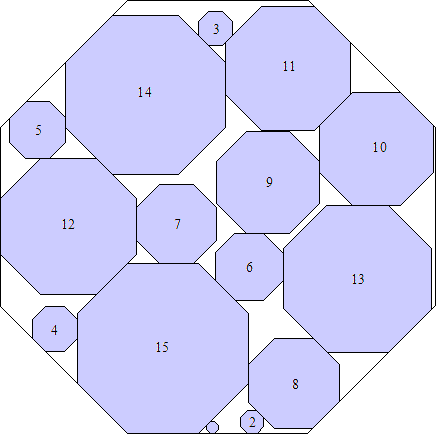
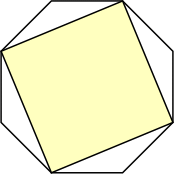
What are the smallest octagons that can contain n non-overlapping unit squares?

Unit Squares In Octagons

s = 1 / √(2+√2)
(Andrew Bayly)
s = .8766+
(Maurizio Morandi)
s = 6 (3 – 2√2)
 
s = 2 / √(2+√2)
 

s = 3 (√2 – 1)
 
s = 7 – 4√2
(Maurizio Morandi)
s = 1.4369+
(Maurizio Morandi)
s = 1.5733+
(Maurizio Morandi)

s = 3 / √(2+√2)
 
s = √(2√2)
(Maurizio Morandi)
s = 1.7533+
(Maurizio Morandi)
s = 5 (√2 – 1)
 

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 12/1/13.