Problem of the Month
(December 2015)

What are the smallest two squares that together contain the squares of sides 1 through n? More precisely, how small can the total area be of at most two squares containing non-overlapping copies of these squares be? Does one of the two optimal squares always contain no more than 1 square?

What are the answers if we consider squares with areas 1 through n instead of sides 1 through n?

ANSWERS

Solutions were received from David Cantrell, George Sicherman, and Maurizio Morandi,

Here are the smallest known packings:

Packing Squares of Side 1 Through n

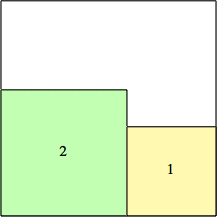
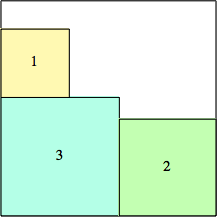
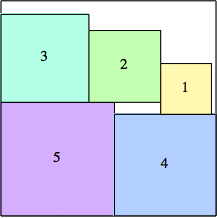
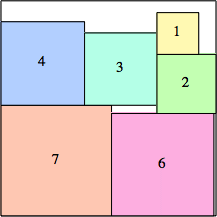
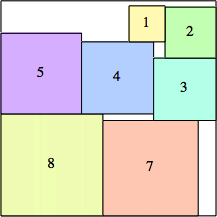
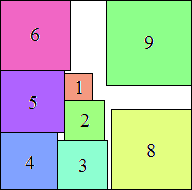
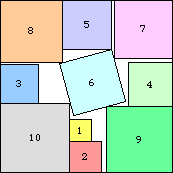
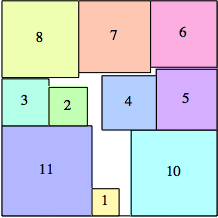
2:   22 + 12 = 5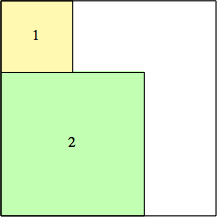
3:   32 + 32 = 18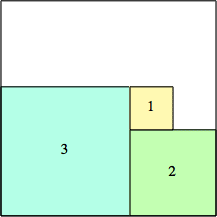
4:   52 + 42 = 41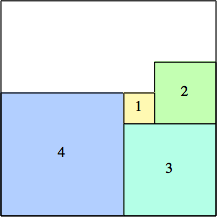
5:   72 + 52 = 74

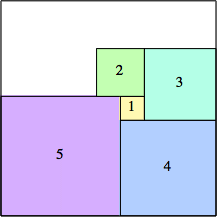6:   92 + 62 = 117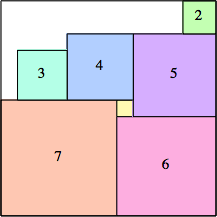
7:   132 = 169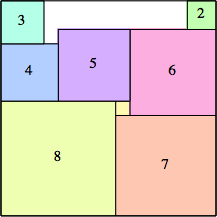
8:   152 = 225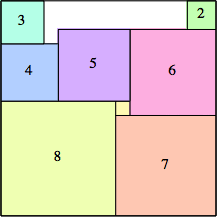
9:   152 + 92 = 306

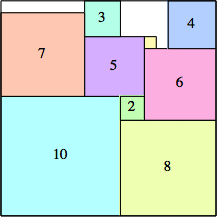10:   182 + 92 = 405
11:   212 + 92 = 522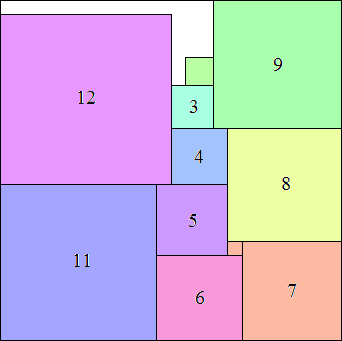
12:   242 + 102 = 676 (MM)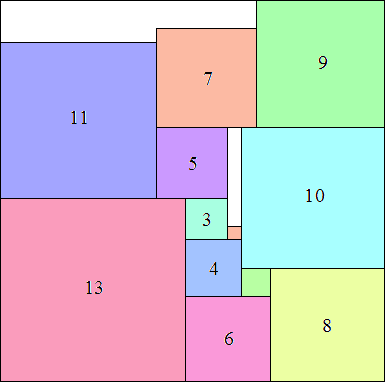
13:   272 + 122 = 873 (MM)

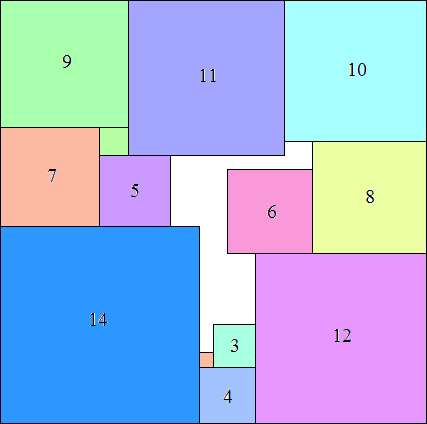14:   302 + 132 = 1069 (MM)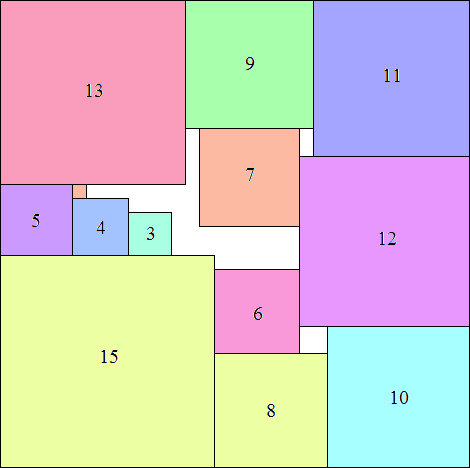
15:   332 + 142 = 1285 (MM)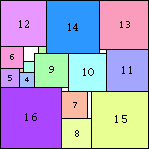
16:   392 = 1521 (MM)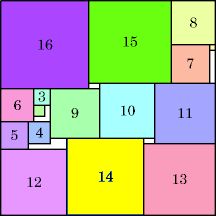
17:   392 + 172 = 1810 (GS)

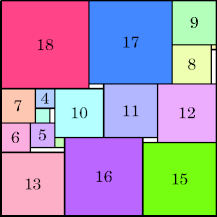18:   442 + 142 = 2132 (GS)
19:   472 + 172 = 2498 (MM)
20:   512 + 172 = 2890 (MM)
21:   562 + 142 = 3332 (MM)

22:   602 + 152 = 3825 (MM)
23:   642 + 162 = 4352 (MM)
24:   662 + 242 = 4932 (MM)
25:   722 + 202 = 5584 (MM)

Packing Squares of Area 1 Through n

2:   √22 + √12
= 3
3:   (√2+√1)2 + √32
= 8.828+
4:   (√3+√2)2 + √42
= 13.898+
5:   (√5+√4)2
= 17.944+

6:   (√5+√4)2 + √62
= 23.944+
7:   (√4+√3+√2)2 + √52
= 31.484+
8:   (√5+√4+√3)2 + √62
= 41.618+
9:   (√6+√5+√4)2 + √72
= 51.696+ (MM)

10:   61.2+
(DC)
11:   (√8+√7+√6)2 + √92
= 71.784+
12:   (√10+√9+√8)2
= 80.832+ (DC)
13:   (√13+√8+√7)2 + √112
= 93.441+ (MM)

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 12/1/15.